5.3解一元一次方程课件(共32张PPT) 冀教版数学七年级上册
文档属性
| 名称 | 5.3解一元一次方程课件(共32张PPT) 冀教版数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 14:54:16 | ||
图片预览











文档简介
(共32张PPT)
5.3 解一元一次方程
第五章 一元一次方程
学习目标
1.掌握解一元一次方程的方法,能够熟练地解一元一次方程;
2.通过一元一次方程的解法及步骤的探究,体会化归思想,发展学生分析问题和解决问题的能力.
我们已经学习了等式的基本性质,怎样运用等式
的这些性质去解一元一次方程呢?
1.合并同类项
解方程:(1)5x=4x-6; (2)3x-2=2x+5.
解:
(1)移项,得:5x-4x=-6,
合并同类项,得x=-6 .
(2) 移项,得:3x-2x=5+2.
合并同类项,得x=7.
例1
小 结
解方程时未知数的系数要化为1.
下列方程移项正确的是( )
A.3x-1=-5移项,得3x=5-1
B.3x-1=-2移项,得3x=-2-1
C.2x+3=4x移项,得4x-2x=3
D.2x+3=3x移项,得2x-3x=3
1
C
【中考·株洲】一元一次方程3x=6的解是( )
A.x=1 B.x=2
C.x=3 D.x=4
若代数式x+3的值为5,则x等于( )
A.2 B.-2 C.8 D.-8
2
B
3
A
小 结
合并同类项时系数加减,字母和字母的指数不变.
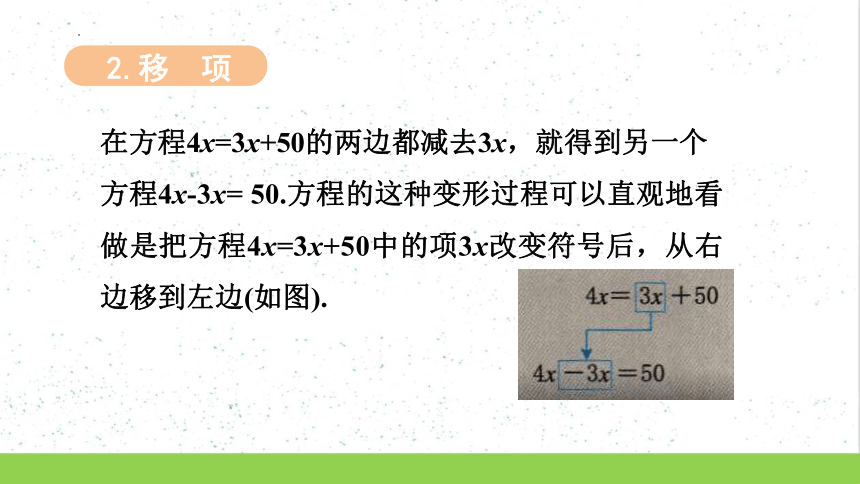
2.移 项
在方程4x=3x+50的两边都减去3x,就得到另一个
方程4x-3x= 50.方程的这种变形过程可以直观地看做是把方程4x=3x+50中的项3x改变符号后,从右边移到左边(如图).
在解方程的过程中,等号的两边加上(或减去)方程中某一项的变形过程,相当于将这一项改变符号后,从等号的一边移到另一边.这种变形过程叫做移项.
定义
将方程6x+3=2x-1移项后,可得( )
A.6x-2x=-3+1
B.6x-2x=-3-1
C.6x+2x=-3-1
D.6x+2x=1-3
例2
B
小 结
移项时,不管是含未知数的项还是常数项都要改变符号,始终记住一句话:移项要变号.
把方程3y-6=y+8变形为3y-y=8+6,这种变形叫做________,依据是______________.
1.
移项
等式的性质1
2
解方程时,移项法则的依据是( )
A.加法交换律 B.加法结合律
C.等式的性质1 D.等式的性质2
C
解下列方程:(1)7x=4x-9;(2) x-2= x+1.
解:
(1)移项,得 7x-4x=-9,
合并同类项,得 3x=-9,
将x的系数化为1,得:x=-3.
(2)移项,得 x- x=1+2,
合并同类项,得 - x=3,
将x的系数化为1,得:x=-9.
例3
已知关于x的方程3a-x= +3的解为2,则式子a2-2a+1的值是________.
1
1
关于x的方程3x+2x=-5与2ax+3a=-3的解相同,则a的值为( )
A. 3 B.- 3 C. D. -
2
B
3.用去括号法解一元一次方程
按照移项法则和去括号法则进行解答,先去括号,再进行移项及合并同类项,注意符号问题.
解方程:3x+2(2x-3)=4-3(x+2).
例4
解:
去括号,得3x+4x-6=4-3x-6.
移项,得 3x+4x+3x=4-6+6.
合并同类项,得 10x=4.
系数化为1,得 x= .
方程中含有括号 时,一般先去括号.
小 结
去括号时,用括号外的因数去乘括号里的每一项,再把积相加,这里易出现括号外的因数只乘括号里的第一项的错误;括号前是“-”,去括号时,括号里的各项都改变符号,这里易出现只改变括号里第一项的符号,而后面项的符号不改变的错误.
将方程3x-5(1+2x)=6去括号,正确的是( )
A.3x-5+10x=6
B. 3x-5+4x=6
C. 3x-5-10x=6
D. 3x-5+10x=6
1
C
【2023·沧州三中月考】解方程-2(2x+1)=x,以下去括号正确的是( )
A.-4x+1=-x B.-4x+2=-x
C.-4x-1=x D.-4x-2=x
2
D
【2022·绍兴】元朝朱世杰的《算学启蒙》一书记载:“良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何追及之.”其题意为:“良马每天行240里,劣马每天行150里,劣马先行12天,良马要几天追上劣马?”答:良马追上劣马需要的天数是________.
3
20
【解析】设良马追上劣马需要x天,
根据题意可列方程 : (12+x)×150=240x,
解得: x=20.
4.用去分母法解一元一次方程
问题1:去分母时,方程两边同乘以一个什么数合适呢?
问题2:像方程 ,分子是多项式,
去分母时应该如何处理?
解方程:
例5
解:
去分母,得 2(x+5)+12=x+3-3(5x-2).
去括号,得2x+10+12=x+3-15x+6.
移项,得2x-x+15x=3+6-12-10.
合并同类项,得16x=-13.
系数化为1,得x=
小 结
解含分母的一元一次方程的关键是去分母,而去分母的关键是找各个分母的最小公倍数,去分母的方法是将方程两边同时乘这个最小公倍数,解这类方程一般要经历:去分母→去括号→移项 →合并同类项→系数化为1.
1
在解方程 的过程中,
①去分母,得1-15x+3=2(2x-1);
②去括号,得1-15x+3=4x- 2;
③移项,得-15x-4x=-2-3-1;
④合并同类项,得-19x=-6;
⑤系数化为1,得x= .
其中开始出现错误的步骤是________.(填序号)
①
方程+=的解是( )
A.x=1 B.x=2 C.x=4 D.x=6
2
【解析】原方程去分母得2(x-1)+x+2=3(4-x),化简得 3x=12-3x,解得x=2,故选B.
B
3
下面解方程的结果正确的是( )
A.方程4=3x-4x的解为x=4
B.方程 x= 的解为x=2
C.方程32=8x的解为x=
D.方程1-4= x的解为x=-9
D
1. 方程中移项:
(1)移项是把方程中的某些项改变符号后从方程的一边
移到方程的另一边;
(2)移项的依据是等式的性质1.
课堂小结
2.解带括号的一元一次方程的一般步骤:
1. 去括号:括号外是“+”号,每项都不变号;括号
外是“-”号,每项都变号.
2. 移项:把含有未知数的项移到方程的一边,其他各
项都移到方程的另一边.
3. 合并同类项:把方程化为“ax=b(a≠0)”的形式.
4. 系数化为1:在方程的两边都除以未知数的系数a,
得到方程的解为x= .
3.用去分母法解方程
1.解含分母的一元一次方程的关键是去分母,而去分母的关键是找各个分母的最小公倍数.
2. 去分母时,分子如果是一个多项式,要将分子作为一个整体加上括号;
3. 去分母时,不含分母的项不要漏乘各分母的最小公倍数;
4. 去括号时,不要出现漏乘现象和符号错误.
谢谢观看
5.3 解一元一次方程
第五章 一元一次方程
学习目标
1.掌握解一元一次方程的方法,能够熟练地解一元一次方程;
2.通过一元一次方程的解法及步骤的探究,体会化归思想,发展学生分析问题和解决问题的能力.
我们已经学习了等式的基本性质,怎样运用等式
的这些性质去解一元一次方程呢?
1.合并同类项
解方程:(1)5x=4x-6; (2)3x-2=2x+5.
解:
(1)移项,得:5x-4x=-6,
合并同类项,得x=-6 .
(2) 移项,得:3x-2x=5+2.
合并同类项,得x=7.
例1
小 结
解方程时未知数的系数要化为1.
下列方程移项正确的是( )
A.3x-1=-5移项,得3x=5-1
B.3x-1=-2移项,得3x=-2-1
C.2x+3=4x移项,得4x-2x=3
D.2x+3=3x移项,得2x-3x=3
1
C
【中考·株洲】一元一次方程3x=6的解是( )
A.x=1 B.x=2
C.x=3 D.x=4
若代数式x+3的值为5,则x等于( )
A.2 B.-2 C.8 D.-8
2
B
3
A
小 结
合并同类项时系数加减,字母和字母的指数不变.
2.移 项
在方程4x=3x+50的两边都减去3x,就得到另一个
方程4x-3x= 50.方程的这种变形过程可以直观地看做是把方程4x=3x+50中的项3x改变符号后,从右边移到左边(如图).
在解方程的过程中,等号的两边加上(或减去)方程中某一项的变形过程,相当于将这一项改变符号后,从等号的一边移到另一边.这种变形过程叫做移项.
定义
将方程6x+3=2x-1移项后,可得( )
A.6x-2x=-3+1
B.6x-2x=-3-1
C.6x+2x=-3-1
D.6x+2x=1-3
例2
B
小 结
移项时,不管是含未知数的项还是常数项都要改变符号,始终记住一句话:移项要变号.
把方程3y-6=y+8变形为3y-y=8+6,这种变形叫做________,依据是______________.
1.
移项
等式的性质1
2
解方程时,移项法则的依据是( )
A.加法交换律 B.加法结合律
C.等式的性质1 D.等式的性质2
C
解下列方程:(1)7x=4x-9;(2) x-2= x+1.
解:
(1)移项,得 7x-4x=-9,
合并同类项,得 3x=-9,
将x的系数化为1,得:x=-3.
(2)移项,得 x- x=1+2,
合并同类项,得 - x=3,
将x的系数化为1,得:x=-9.
例3
已知关于x的方程3a-x= +3的解为2,则式子a2-2a+1的值是________.
1
1
关于x的方程3x+2x=-5与2ax+3a=-3的解相同,则a的值为( )
A. 3 B.- 3 C. D. -
2
B
3.用去括号法解一元一次方程
按照移项法则和去括号法则进行解答,先去括号,再进行移项及合并同类项,注意符号问题.
解方程:3x+2(2x-3)=4-3(x+2).
例4
解:
去括号,得3x+4x-6=4-3x-6.
移项,得 3x+4x+3x=4-6+6.
合并同类项,得 10x=4.
系数化为1,得 x= .
方程中含有括号 时,一般先去括号.
小 结
去括号时,用括号外的因数去乘括号里的每一项,再把积相加,这里易出现括号外的因数只乘括号里的第一项的错误;括号前是“-”,去括号时,括号里的各项都改变符号,这里易出现只改变括号里第一项的符号,而后面项的符号不改变的错误.
将方程3x-5(1+2x)=6去括号,正确的是( )
A.3x-5+10x=6
B. 3x-5+4x=6
C. 3x-5-10x=6
D. 3x-5+10x=6
1
C
【2023·沧州三中月考】解方程-2(2x+1)=x,以下去括号正确的是( )
A.-4x+1=-x B.-4x+2=-x
C.-4x-1=x D.-4x-2=x
2
D
【2022·绍兴】元朝朱世杰的《算学启蒙》一书记载:“良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何追及之.”其题意为:“良马每天行240里,劣马每天行150里,劣马先行12天,良马要几天追上劣马?”答:良马追上劣马需要的天数是________.
3
20
【解析】设良马追上劣马需要x天,
根据题意可列方程 : (12+x)×150=240x,
解得: x=20.
4.用去分母法解一元一次方程
问题1:去分母时,方程两边同乘以一个什么数合适呢?
问题2:像方程 ,分子是多项式,
去分母时应该如何处理?
解方程:
例5
解:
去分母,得 2(x+5)+12=x+3-3(5x-2).
去括号,得2x+10+12=x+3-15x+6.
移项,得2x-x+15x=3+6-12-10.
合并同类项,得16x=-13.
系数化为1,得x=
小 结
解含分母的一元一次方程的关键是去分母,而去分母的关键是找各个分母的最小公倍数,去分母的方法是将方程两边同时乘这个最小公倍数,解这类方程一般要经历:去分母→去括号→移项 →合并同类项→系数化为1.
1
在解方程 的过程中,
①去分母,得1-15x+3=2(2x-1);
②去括号,得1-15x+3=4x- 2;
③移项,得-15x-4x=-2-3-1;
④合并同类项,得-19x=-6;
⑤系数化为1,得x= .
其中开始出现错误的步骤是________.(填序号)
①
方程+=的解是( )
A.x=1 B.x=2 C.x=4 D.x=6
2
【解析】原方程去分母得2(x-1)+x+2=3(4-x),化简得 3x=12-3x,解得x=2,故选B.
B
3
下面解方程的结果正确的是( )
A.方程4=3x-4x的解为x=4
B.方程 x= 的解为x=2
C.方程32=8x的解为x=
D.方程1-4= x的解为x=-9
D
1. 方程中移项:
(1)移项是把方程中的某些项改变符号后从方程的一边
移到方程的另一边;
(2)移项的依据是等式的性质1.
课堂小结
2.解带括号的一元一次方程的一般步骤:
1. 去括号:括号外是“+”号,每项都不变号;括号
外是“-”号,每项都变号.
2. 移项:把含有未知数的项移到方程的一边,其他各
项都移到方程的另一边.
3. 合并同类项:把方程化为“ax=b(a≠0)”的形式.
4. 系数化为1:在方程的两边都除以未知数的系数a,
得到方程的解为x= .
3.用去分母法解方程
1.解含分母的一元一次方程的关键是去分母,而去分母的关键是找各个分母的最小公倍数.
2. 去分母时,分子如果是一个多项式,要将分子作为一个整体加上括号;
3. 去分母时,不含分母的项不要漏乘各分母的最小公倍数;
4. 去括号时,不要出现漏乘现象和符号错误.
谢谢观看
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
