第七章 平行线的证明复习课课件 (共20张PPT)北师大版八年级上册数学
文档属性
| 名称 | 第七章 平行线的证明复习课课件 (共20张PPT)北师大版八年级上册数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 457.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 14:59:14 | ||
图片预览





文档简介
(共20张PPT)
复习课
01
第七章 平行线的证明
一、学习目标
1.理解证明的必要性,知道综合法证明的格式,体会证明的过程要步步有依据
2.通过具体实例了解定义、命题、定理、公理的含义,会区分命题的条件和结论,会通过反例判定一个命题是假命题
3.会应用数学语言表示平行线的判定及性质,知道三角形内角和定理及推论,会灵活运用它们解决实际问题
三、知识梳理
(一)命题
2. 命题有真有假,其中正确的命题叫做真命题;错误的命题叫做假命题.
3. 要说明一个命题是假命题,只要举出一个符合命题条件,但不符合命题结论的例子就可以,像这样的例子称为反例.
1.判断一件事情的句子叫做命题.
三、知识梳理
4.每个命题都是由条件和结论两部分组成.命题一般写成“如果……,那么……”的形式,“如果”引出的部分是条件,“那么”引出的部分是结论.
5.经过实践验证的真命题称为基本事实.
6. 经过演绎推理得到的重要的真命题叫做定理.
三、知识梳理
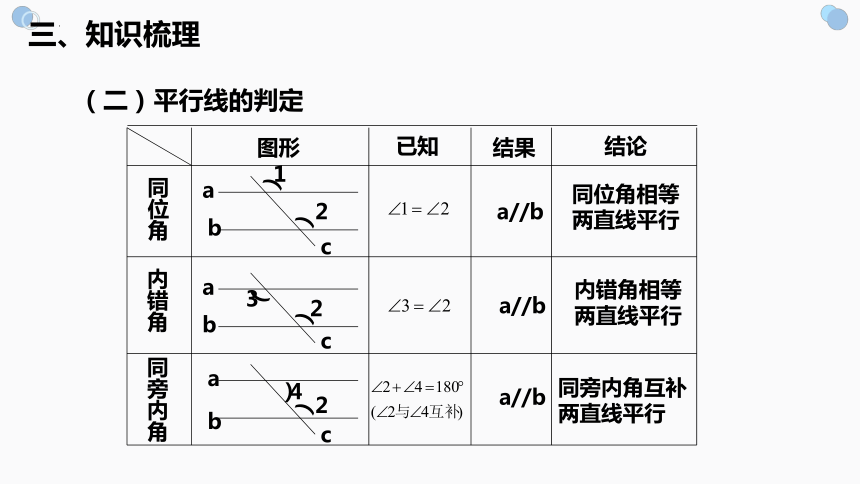
(二)平行线的判定
图形
已知
结果
结论
同位角
内错角
同旁内角
a//b
a//b
a//b
同位角相等
两直线平行
内错角相等
两直线平行
同旁内角互补
两直线平行
1
2
)
)
a
b
c
2
3
)
)
a
b
c
2
4
)
)
a
b
c
三、知识梳理
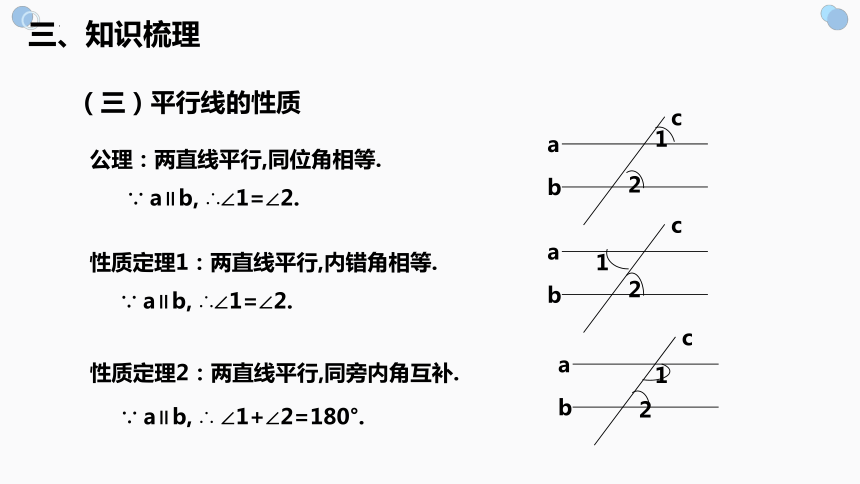
(三)平行线的性质
公理:两直线平行,同位角相等.
∵ a∥b, ∴∠1=∠2.
性质定理1:两直线平行,内错角相等.
∵ a∥b, ∴∠1=∠2.
性质定理2:两直线平行,同旁内角互补.
∵ a∥b, ∴ ∠1+∠2=180°.
a
b
c
2
1
a
b
c
1
2
a
b
c
1
2
三、知识梳理
(四)三角形内角和定理
定理:三角形的内角和等于180°.
推论1:三角形的一个外角等于和它不相邻的两个内角的和.
推论2:三角形的一个外角大于任何一个和它不相邻的内角.
四、典型例题
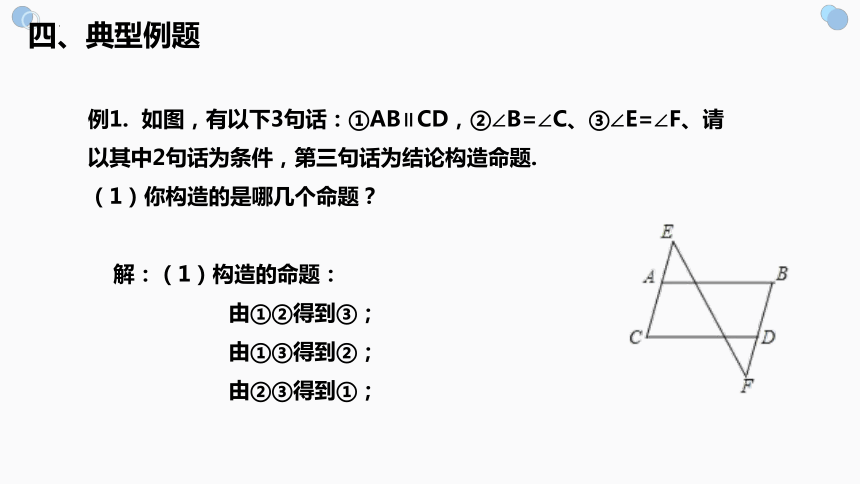
例1. 如图,有以下3句话:①AB∥CD,②∠B=∠C、③∠E=∠F、请以其中2句话为条件,第三句话为结论构造命题.
(1)你构造的是哪几个命题?
解:(1)构造的命题:
由①②得到③;
由①③得到②;
由②③得到①;
四、典型例题
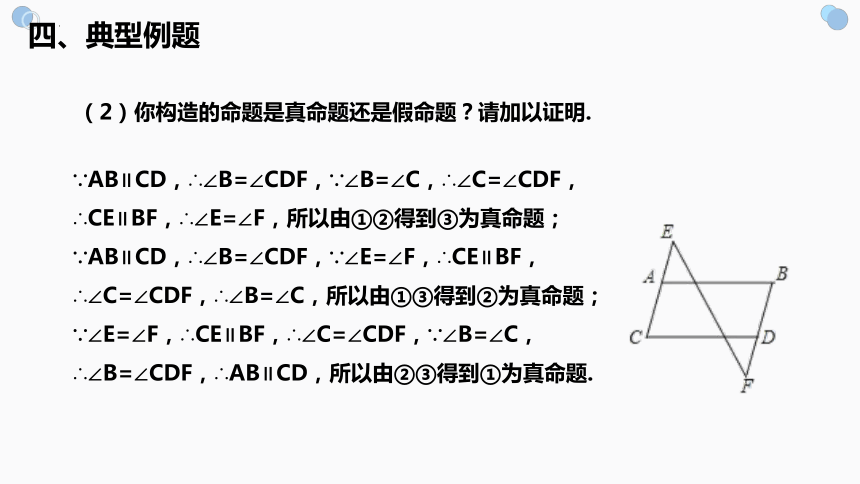
(2)你构造的命题是真命题还是假命题?请加以证明.
∵AB∥CD,∴∠B=∠CDF,∵∠B=∠C,∴∠C=∠CDF,
∴CE∥BF,∴∠E=∠F,所以由①②得到③为真命题;
∵AB∥CD,∴∠B=∠CDF,∵∠E=∠F,∴CE∥BF,
∴∠C=∠CDF,∴∠B=∠C,所以由①③得到②为真命题;
∵∠E=∠F,∴CE∥BF,∴∠C=∠CDF,∵∠B=∠C,
∴∠B=∠CDF,∴AB∥CD,所以由②③得到①为真命题.
【当堂检测】
1.命题“垂直于同一条直线的两条直线互相平行”的题设是( )
A. 垂直
B. 两条直线
C. 同一条直线
D. 两条直线垂直于同一条直线
D
例2.如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
四、典型例题
解:(1)平行;
理由:∵∠2+∠CDB=180°,∠1+∠2=180°,
∴∠CDB=∠1,
∴AE∥FC.
(2)AD与BC的位置关系如何?为什么?
四、典型例题
(2)平行,
证明:∵AE∥FC,
∴∠CDA+∠DAE=180°,
∵∠DAE=∠BCF
∴∠CDA+∠BCF=180°,
∴AD∥BC.
(3)BC平分∠DBE吗?为什么.
四、典型例题
(3)平分,
证明:∵AE∥FC,
∴∠EBC=∠BCF,
∵AD∥BC,
∴∠BCF=∠FDA,∠DBC=∠BDA,
又∵DA平分∠BDF,即∠FDA=∠BDA,
∴∠EBC=∠DBC,
∴BC平分∠DBE.
【当堂检测】
2.如图,AB∥EF∥CD,∠ABC=46°,∠CEF=154°,则∠BCE等于( )
A.23° B.16° C.20° D.26°
C
【当堂检测】
3.如图,将一副三角板按如图放置,则下列结论
①∠1=∠3;②如果∠2=30°,则有AC∥DE;
③如果∠2=30°,则有BC∥AD;④如果∠2=30°,必有∠4=∠C.
其中正确的有 .(填序号)
①②④
四、典型例题
例3.如图所示,在△ABC中,已知AD是角平分线,∠B=66°,∠C=54°.
(1)求∠ADB的度数;
解:(1)∵在△ABC中,∠B=66°,∠C=54°,
∴∠BAC=180°-∠B-∠C=60°.
∵AD是∠BAC的平分线,
∴∠BAD= ∠BAC=30°.
在△ABD中,∠B=66°,∠BAD=30°,
∴∠ADB=180°-∠B-∠BAD=84°.
四、典型例题
∵∠CAD= ∠BAC=30°,DE⊥AC,
∴∠ADE=90°-∠EAD=60°.
(2)若DE⊥AC于点E,求∠ADE的度数.
【当堂检测】
4.如图,在△ABC中,AD是BC边上的高线,CE是一条角平分线,且相交于点P.已知∠APE=55°,∠AEP=80°,∠B的度数是多少?
A
B
C
D
E
P
解:∵AD⊥BC,∴∠PDC=90°,
∵∠CPD=∠APE=55°,
∴∠PCD=90°-55°=35°,
∵∠AEP=∠B+∠ECB,
∴∠B=80°-35°=45°,
故∠B的度数是为45°.
【当堂检测】
5.如图,在△ABC中,∠BAC=90°,BD平分∠ABC,CD∥AB交BD于点D,已知∠D=29°,则∠1的度数为多少?
A
B
C
D
1
(
解:∵CD∥AB,∠D=29°,∴∠ABD=∠D=29°
又∵BD平分∠ABC,∴∠ABC=2∠ABD=58°,
∵CD∥AB,∠BAC=90°,
∴∠ACD=∠BAC=90°,∠ABC+∠BCD=180°,
∴∠BCD=180°-∠ABC=122°,
∴∠1=∠BCD-∠ACD=122°-90°=32°.
五、课堂总结
本章总结:
1.命题与证明的相关概念
2.平行线的判定与性质
3.三角形的内角和定理及其推论
复习课
01
第七章 平行线的证明
一、学习目标
1.理解证明的必要性,知道综合法证明的格式,体会证明的过程要步步有依据
2.通过具体实例了解定义、命题、定理、公理的含义,会区分命题的条件和结论,会通过反例判定一个命题是假命题
3.会应用数学语言表示平行线的判定及性质,知道三角形内角和定理及推论,会灵活运用它们解决实际问题
三、知识梳理
(一)命题
2. 命题有真有假,其中正确的命题叫做真命题;错误的命题叫做假命题.
3. 要说明一个命题是假命题,只要举出一个符合命题条件,但不符合命题结论的例子就可以,像这样的例子称为反例.
1.判断一件事情的句子叫做命题.
三、知识梳理
4.每个命题都是由条件和结论两部分组成.命题一般写成“如果……,那么……”的形式,“如果”引出的部分是条件,“那么”引出的部分是结论.
5.经过实践验证的真命题称为基本事实.
6. 经过演绎推理得到的重要的真命题叫做定理.
三、知识梳理
(二)平行线的判定
图形
已知
结果
结论
同位角
内错角
同旁内角
a//b
a//b
a//b
同位角相等
两直线平行
内错角相等
两直线平行
同旁内角互补
两直线平行
1
2
)
)
a
b
c
2
3
)
)
a
b
c
2
4
)
)
a
b
c
三、知识梳理
(三)平行线的性质
公理:两直线平行,同位角相等.
∵ a∥b, ∴∠1=∠2.
性质定理1:两直线平行,内错角相等.
∵ a∥b, ∴∠1=∠2.
性质定理2:两直线平行,同旁内角互补.
∵ a∥b, ∴ ∠1+∠2=180°.
a
b
c
2
1
a
b
c
1
2
a
b
c
1
2
三、知识梳理
(四)三角形内角和定理
定理:三角形的内角和等于180°.
推论1:三角形的一个外角等于和它不相邻的两个内角的和.
推论2:三角形的一个外角大于任何一个和它不相邻的内角.
四、典型例题
例1. 如图,有以下3句话:①AB∥CD,②∠B=∠C、③∠E=∠F、请以其中2句话为条件,第三句话为结论构造命题.
(1)你构造的是哪几个命题?
解:(1)构造的命题:
由①②得到③;
由①③得到②;
由②③得到①;
四、典型例题
(2)你构造的命题是真命题还是假命题?请加以证明.
∵AB∥CD,∴∠B=∠CDF,∵∠B=∠C,∴∠C=∠CDF,
∴CE∥BF,∴∠E=∠F,所以由①②得到③为真命题;
∵AB∥CD,∴∠B=∠CDF,∵∠E=∠F,∴CE∥BF,
∴∠C=∠CDF,∴∠B=∠C,所以由①③得到②为真命题;
∵∠E=∠F,∴CE∥BF,∴∠C=∠CDF,∵∠B=∠C,
∴∠B=∠CDF,∴AB∥CD,所以由②③得到①为真命题.
【当堂检测】
1.命题“垂直于同一条直线的两条直线互相平行”的题设是( )
A. 垂直
B. 两条直线
C. 同一条直线
D. 两条直线垂直于同一条直线
D
例2.如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
四、典型例题
解:(1)平行;
理由:∵∠2+∠CDB=180°,∠1+∠2=180°,
∴∠CDB=∠1,
∴AE∥FC.
(2)AD与BC的位置关系如何?为什么?
四、典型例题
(2)平行,
证明:∵AE∥FC,
∴∠CDA+∠DAE=180°,
∵∠DAE=∠BCF
∴∠CDA+∠BCF=180°,
∴AD∥BC.
(3)BC平分∠DBE吗?为什么.
四、典型例题
(3)平分,
证明:∵AE∥FC,
∴∠EBC=∠BCF,
∵AD∥BC,
∴∠BCF=∠FDA,∠DBC=∠BDA,
又∵DA平分∠BDF,即∠FDA=∠BDA,
∴∠EBC=∠DBC,
∴BC平分∠DBE.
【当堂检测】
2.如图,AB∥EF∥CD,∠ABC=46°,∠CEF=154°,则∠BCE等于( )
A.23° B.16° C.20° D.26°
C
【当堂检测】
3.如图,将一副三角板按如图放置,则下列结论
①∠1=∠3;②如果∠2=30°,则有AC∥DE;
③如果∠2=30°,则有BC∥AD;④如果∠2=30°,必有∠4=∠C.
其中正确的有 .(填序号)
①②④
四、典型例题
例3.如图所示,在△ABC中,已知AD是角平分线,∠B=66°,∠C=54°.
(1)求∠ADB的度数;
解:(1)∵在△ABC中,∠B=66°,∠C=54°,
∴∠BAC=180°-∠B-∠C=60°.
∵AD是∠BAC的平分线,
∴∠BAD= ∠BAC=30°.
在△ABD中,∠B=66°,∠BAD=30°,
∴∠ADB=180°-∠B-∠BAD=84°.
四、典型例题
∵∠CAD= ∠BAC=30°,DE⊥AC,
∴∠ADE=90°-∠EAD=60°.
(2)若DE⊥AC于点E,求∠ADE的度数.
【当堂检测】
4.如图,在△ABC中,AD是BC边上的高线,CE是一条角平分线,且相交于点P.已知∠APE=55°,∠AEP=80°,∠B的度数是多少?
A
B
C
D
E
P
解:∵AD⊥BC,∴∠PDC=90°,
∵∠CPD=∠APE=55°,
∴∠PCD=90°-55°=35°,
∵∠AEP=∠B+∠ECB,
∴∠B=80°-35°=45°,
故∠B的度数是为45°.
【当堂检测】
5.如图,在△ABC中,∠BAC=90°,BD平分∠ABC,CD∥AB交BD于点D,已知∠D=29°,则∠1的度数为多少?
A
B
C
D
1
(
解:∵CD∥AB,∠D=29°,∴∠ABD=∠D=29°
又∵BD平分∠ABC,∴∠ABC=2∠ABD=58°,
∵CD∥AB,∠BAC=90°,
∴∠ACD=∠BAC=90°,∠ABC+∠BCD=180°,
∴∠BCD=180°-∠ABC=122°,
∴∠1=∠BCD-∠ACD=122°-90°=32°.
五、课堂总结
本章总结:
1.命题与证明的相关概念
2.平行线的判定与性质
3.三角形的内角和定理及其推论
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
