15.4 角的平分线 课件 (共21张PPT)沪教版(五四 制)数学八年级上册
文档属性
| 名称 | 15.4 角的平分线 课件 (共21张PPT)沪教版(五四 制)数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 15:00:35 | ||
图片预览







文档简介
(共21张PPT)
1.观看角平分仪视频,能说出角平分仪平分角的依据是
构建两个三角形全等;
2.通过观察、分析,能证明所作射线是角平分线;
3.能用直尺和圆规作已知角的平分线,并能用语言描述作图步骤;
4.通过合作交流,类比角平分线的尺规作图,绝大多数同学会用
直尺和圆规作“过一点作已知直线的垂线”。
教学目标
情景引入
从一个角的顶点引出一条射线,把这个角分成两个完全相同的
角,这条射线叫做这个角的角平分线
你会画角平
分线吗
问题1:在一张半透明的纸上画一个角,在不借
助任何工具的情况下,你能找到这个角的平分线吗
角是轴对称图形.
角平分线所在的直线是它的对称轴.
方法一:折叠法
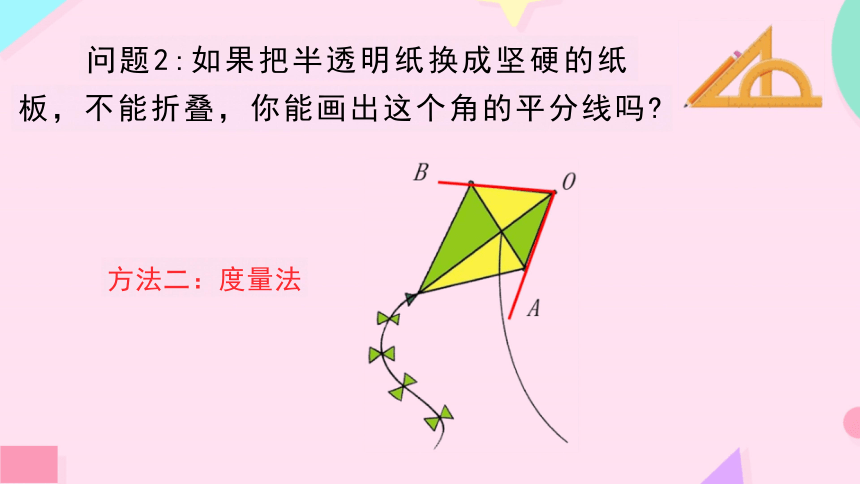
问题2:如果把半透明纸换成坚硬的纸
板,不能折叠,你能画出这个角的平分线吗
方法二:度量法
新知探究
方法三:角平分仪
你能说明角
平分仪平分 角的原理吗
工程上答想得到一个角的角干分线
已知:如图,已知AB=AD,BC =DC .
求证:AE 平分∠DAB.
方法四:尺规法
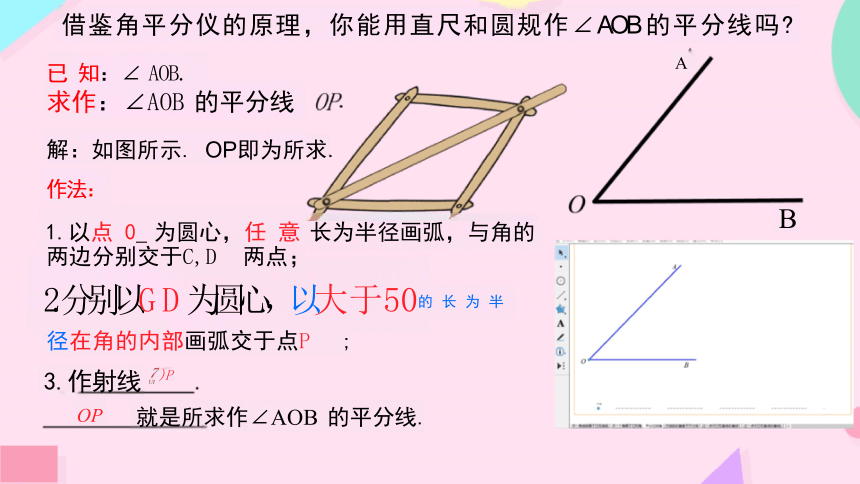
借鉴角平分仪的原理,你能用直尺和圆规作∠AOB的
规:圆规 — — 画圆、弧, 截取相等线段
尺:没有刻度的直尺 —— 画线
平分线吗
尺规
已 知:∠ AOB.
求作:∠AOB 的平分线
解:如图所示. OP即为所求.
作法:
1.以点 0_ 为圆心,任 意 长为半径画弧,与角的 两边分别交于C,D 两点;
2.分别以GD为圆心,以大于50的长为半
径在角的内部画弧交于点P ;
3.作射线 )P
OP 就是所求作∠AOB 的平分线.
A
B
借鉴角平分仪的原理,你能用直尺和圆规作∠AOB 的平分线吗
小组合作
利用直尺和圆规,动手画一画
∠AOB的平分线,帮助小明解决问题
步骤
画弧
别文
探究之旅:尺规作图
作一钝角∠AOB, 用尺规在∠AOB 内部作∠AOE=
如图,根据尺规作图所留痕迹,可以求出∠ADC =( ).
A.60° B.70° C.110° D.120°
工人师傅常用角尺平分一个任意角,做法是:如图所示,∠AOB
是一个任意角,在边OA,OB 上分别取OM=ON, 移动角尺,使角尺
两边相同的刻度分别与M,N 重合,得到∠AOB 的平分线OP, 做法中
用到三角形全等的判定方法是( )
A.SSS
C.ASA
B.SAS
D.HL
请在练习本上用尺规作△ABC 三个内角的角平分线.
观察看看有什么特点
一定正确的个数有( )个.
①∠AOP =∠BOP; ②OC =PC;
③ OA//DP; ④OP 是线段CD 的垂直平分线.
A.1 B.2 C.3 D.4
尺规作图作∠AOB 的平分线如下:以0为圆心,任意长为半径画
弧交OA、OB 于C 、D, 再分别以点C、D 为圆心, 大 一 CD
长为半径画弧,两弧交于P, 作射线OP, 连结CD, 则下列结论
变式拓展
经过直线上一点作这条直线的垂线
已知∠AOB 是平角,请你用尺规作∠AOB 的平分线.
这时的角平分线与直线AB 是怎样的位置关系
已知:直线AB 和AB 上一点0.
求作:过点0作AB 的垂线.
A O B
作法:
①以点P 为圆心,以大于点P 到直线AB
的距离的线段长为半径画弧,交直线AB 于点C,D;
②分别以C,D 为圆心,以大 于 2CD
的长为半径画弧,两弧相交于点0;
小组展示
探究:
现衡你霾戴“经箱康线上一点作这条直线的垂线”的方法了,
那莱铽-+碱旌垂缝过值褒绎过点作这条直线的垂线”吧!
③过点0作直线OP, 则直线OP 为所求作的垂线.
P
A
B
(1)作已知角的平分线 建根糖*三选好应和等的两个些角形
玺等线规垄等三角形的对应滑相等要的原理莱溴的满足的条件
(2)在作图步骤的第二步丝定要注意是颐失于某祭线段的,长为
半径作圆弧的,否则两弧没有交点或两弧交点不明显.
(3)通过作图了解三角形三个内角的平分线相交于一点.
请你来说一说
感受到“一法多解”的乐趣
体会了数学中的化归思想
反思总结
基础题:
利用尺规作一个等于45°的角(并保留作图痕迹).
能力突破题:
用尺规作图,不写作法,保留作图痕迹:
已知线段a=3cm,b=4cm, 以 a,b 为直角边作直角三角形.
作业布置
创新挑战题:
光遇到水面、玻璃以及其他许多物体的表面都会
发生反射.当光在两种物质分界面上改变传播方向又 返回原来物质中的现象,叫做光的反射.光的反射遵
循光的反射定律: (1)反射光线与入射光线、法线
(与镜面垂直的线)在同一平面上; (2)反射光线 和入射光线分居在法线的两侧; (3)反射角等于入
射角.
如图,已知入射光线和反射光线,请你用作图的
方法确定平面镜的位置.(保留作图痕迹)
光的反射
法线
反射光线 入射光线
反射角 入射角
镜面
作业布置
1.观看角平分仪视频,能说出角平分仪平分角的依据是
构建两个三角形全等;
2.通过观察、分析,能证明所作射线是角平分线;
3.能用直尺和圆规作已知角的平分线,并能用语言描述作图步骤;
4.通过合作交流,类比角平分线的尺规作图,绝大多数同学会用
直尺和圆规作“过一点作已知直线的垂线”。
教学目标
情景引入
从一个角的顶点引出一条射线,把这个角分成两个完全相同的
角,这条射线叫做这个角的角平分线
你会画角平
分线吗
问题1:在一张半透明的纸上画一个角,在不借
助任何工具的情况下,你能找到这个角的平分线吗
角是轴对称图形.
角平分线所在的直线是它的对称轴.
方法一:折叠法
问题2:如果把半透明纸换成坚硬的纸
板,不能折叠,你能画出这个角的平分线吗
方法二:度量法
新知探究
方法三:角平分仪
你能说明角
平分仪平分 角的原理吗
工程上答想得到一个角的角干分线
已知:如图,已知AB=AD,BC =DC .
求证:AE 平分∠DAB.
方法四:尺规法
借鉴角平分仪的原理,你能用直尺和圆规作∠AOB的
规:圆规 — — 画圆、弧, 截取相等线段
尺:没有刻度的直尺 —— 画线
平分线吗
尺规
已 知:∠ AOB.
求作:∠AOB 的平分线
解:如图所示. OP即为所求.
作法:
1.以点 0_ 为圆心,任 意 长为半径画弧,与角的 两边分别交于C,D 两点;
2.分别以GD为圆心,以大于50的长为半
径在角的内部画弧交于点P ;
3.作射线 )P
OP 就是所求作∠AOB 的平分线.
A
B
借鉴角平分仪的原理,你能用直尺和圆规作∠AOB 的平分线吗
小组合作
利用直尺和圆规,动手画一画
∠AOB的平分线,帮助小明解决问题
步骤
画弧
别文
探究之旅:尺规作图
作一钝角∠AOB, 用尺规在∠AOB 内部作∠AOE=
如图,根据尺规作图所留痕迹,可以求出∠ADC =( ).
A.60° B.70° C.110° D.120°
工人师傅常用角尺平分一个任意角,做法是:如图所示,∠AOB
是一个任意角,在边OA,OB 上分别取OM=ON, 移动角尺,使角尺
两边相同的刻度分别与M,N 重合,得到∠AOB 的平分线OP, 做法中
用到三角形全等的判定方法是( )
A.SSS
C.ASA
B.SAS
D.HL
请在练习本上用尺规作△ABC 三个内角的角平分线.
观察看看有什么特点
一定正确的个数有( )个.
①∠AOP =∠BOP; ②OC =PC;
③ OA//DP; ④OP 是线段CD 的垂直平分线.
A.1 B.2 C.3 D.4
尺规作图作∠AOB 的平分线如下:以0为圆心,任意长为半径画
弧交OA、OB 于C 、D, 再分别以点C、D 为圆心, 大 一 CD
长为半径画弧,两弧交于P, 作射线OP, 连结CD, 则下列结论
变式拓展
经过直线上一点作这条直线的垂线
已知∠AOB 是平角,请你用尺规作∠AOB 的平分线.
这时的角平分线与直线AB 是怎样的位置关系
已知:直线AB 和AB 上一点0.
求作:过点0作AB 的垂线.
A O B
作法:
①以点P 为圆心,以大于点P 到直线AB
的距离的线段长为半径画弧,交直线AB 于点C,D;
②分别以C,D 为圆心,以大 于 2CD
的长为半径画弧,两弧相交于点0;
小组展示
探究:
现衡你霾戴“经箱康线上一点作这条直线的垂线”的方法了,
那莱铽-+碱旌垂缝过值褒绎过点作这条直线的垂线”吧!
③过点0作直线OP, 则直线OP 为所求作的垂线.
P
A
B
(1)作已知角的平分线 建根糖*三选好应和等的两个些角形
玺等线规垄等三角形的对应滑相等要的原理莱溴的满足的条件
(2)在作图步骤的第二步丝定要注意是颐失于某祭线段的,长为
半径作圆弧的,否则两弧没有交点或两弧交点不明显.
(3)通过作图了解三角形三个内角的平分线相交于一点.
请你来说一说
感受到“一法多解”的乐趣
体会了数学中的化归思想
反思总结
基础题:
利用尺规作一个等于45°的角(并保留作图痕迹).
能力突破题:
用尺规作图,不写作法,保留作图痕迹:
已知线段a=3cm,b=4cm, 以 a,b 为直角边作直角三角形.
作业布置
创新挑战题:
光遇到水面、玻璃以及其他许多物体的表面都会
发生反射.当光在两种物质分界面上改变传播方向又 返回原来物质中的现象,叫做光的反射.光的反射遵
循光的反射定律: (1)反射光线与入射光线、法线
(与镜面垂直的线)在同一平面上; (2)反射光线 和入射光线分居在法线的两侧; (3)反射角等于入
射角.
如图,已知入射光线和反射光线,请你用作图的
方法确定平面镜的位置.(保留作图痕迹)
光的反射
法线
反射光线 入射光线
反射角 入射角
镜面
作业布置
