第一章 勾股定理 复习课件 (共21张PPT)北师大版数学八年级上册
文档属性
| 名称 | 第一章 勾股定理 复习课件 (共21张PPT)北师大版数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 01:41:03 | ||
图片预览







文档简介
(共21张PPT)
第一章 勾股定理
第一章 复习课
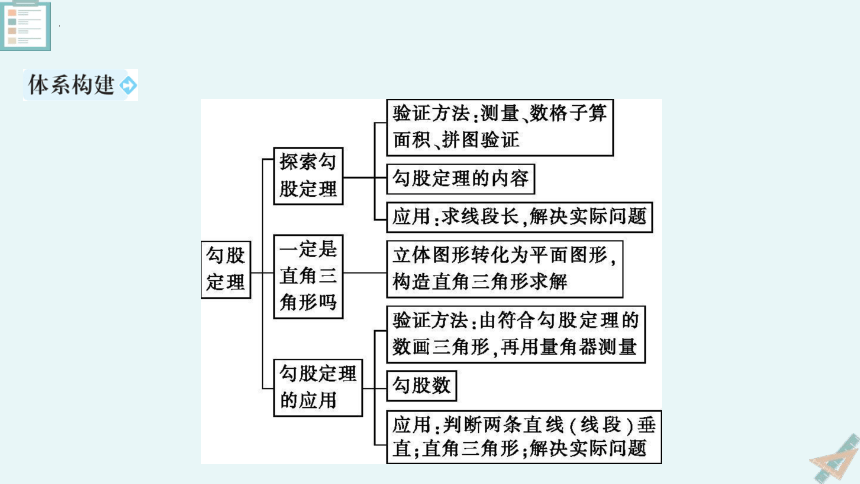
1.知道勾股定理及直角三角形的判别条件(即勾股定理的逆定理),会灵活应用它解决简单的几何问题和生活实际问题.
2.能把简单的立体图形转化为平面图形,构造直角三角形求线段长.
◎重点:能运用勾股定理及直角三角形的判别条件解决简单的实际问题.
勾股定理是几何学中一颗璀璨的“明星”,它凝聚了一代又一代数学家的智慧和心血,本节课,我们共同梳理知识点,构建知识网络.
1.直角三角形两直角边的平方和等于斜边的 平方和 ,即对于任意的直角三角形,如果它的两条直角边分别为a、b,斜边为c,那么一定有a2+b2=c2,这就是 勾股定理 .?
2.勾股定理的验证,可以采用测量、数格子、 割补法 ,通过构造 几何图形 ,并计算 图形面积 得出一个等式,从而验证勾股定理.?
3.勾股定理的逆定理是用来判断一个三角形是否是 直角三角形 ,应用时首先确定该三角形的 最长边 ,当 其余两边的平方和等于最长边的平方 时,该三角形才是直角三角形.?
勾股定理的(有关计算)运用
1.现有两根铁棒,它们的长分别为9 cm和12 cm,如果将这两根铁棒作为直角边焊接成一个直角三角形的铁架,那么第三根铁棒的长应为 ( A )
A.15 cm
B.21 cm
C.25 cm
D.无法确定
A
判定是否为直角三角形
2.在下列长度的各组线段中,能组成直角三角形的是 ( C )
A.5 cm,6 cm,7 cm
B.1 cm,4 cm,9 cm
C.5 cm,12 cm,13 cm
D.5 cm,11 cm,12 cm
C
勾股定理解决实际问题
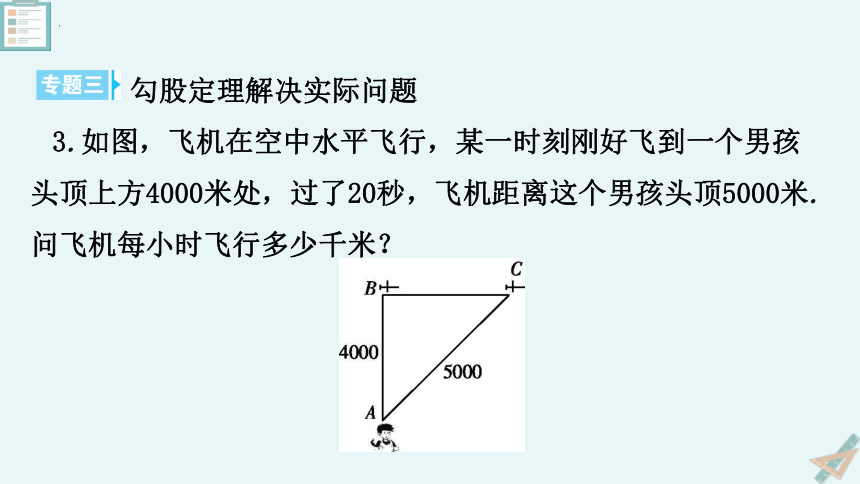
3.如图,飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方4000米处,过了20秒,飞机距离这个男孩头顶5000米.问飞机每小时飞行多少千米?
解:在Rt△ABC中,根据勾股定理可知,
BC2=50002-40002=30002,所以BC=3000米,
3000÷20=150米/秒=540千米/时.
所以飞机每小时飞行540千米.
用于证明两条线段相互垂直
4.如图,在正方形ABCD中,F为DC的中点,E为BC上一点,且EC=????????BC.
?
(1)说明AF与EF的位置关系,并说明理由.
(2)若此正方形的面积是16,求AE的长.
解:(1)如图,连接AE,设EC=a,在正方形ABCD中,因为EC=????????BC,所以BC=4a.所以AD=CD=AB=4a,所以BE=3a.因为F是CD中点,所以DF=CF=2a.
?
在Rt△ABE中,AE2=AB2+BE2=(4a)2+(3a)2=25a2.
同理,在Rt△ADF和Rt△ECF中,AF2=AD2+DF2=(4a)2+(2a)2=20a2,
在Rt△ABE中,AE2=AB2+BE2=(4a)2+(3a)2=25a2.
同理,在Rt△ADF和Rt△ECF中,AF2=AD2+DF2=(4a)2+
(2a)2=20a2,EF2= CE2 +CF2 =a2+(2a)2=5a2,
EF2=5a2,所以AE2=AF2+EF2,所以∠EFA=90°,即AF⊥EF.
(2)因为正方形的面积为16,所以a=1,所以AE2=25a2=25,所以AE=5.
所以AE2=AF2+EF2,所以∠EFA=90°,即
AF⊥EF.
求线段最短问题
5.如图,小河的同一侧有A、B两个小镇,它们到小河所在直线MN的距离分别为BF=2 km,AG=5 km,FG=24 km,要在小河上修建一座小型发电站E,为了节约资源,使得拉到A、B两镇的电线长之和最短,这个电线长之和最短是多少?
解:如图,作点B关于MN的对称点C,并连接AC交MN于点E,连接BE,所以BE+AE=CE+AE=AC.延长AG到D使DG=FC,并连接CD,由已知可知DG=FC=BF=2 km,所以AD=AG+DG=7 km,又因为CD=FG=24 km,在Rt△ADC中,AC2=AD2+CD2=242+72=625,所以AC=25 km,
所以BE+AE=AC=25 km.
1.如图,在△ABC中,∠C=90°,AC=4,BC=2.以AB为一条边向三角形外部作正方形,则正方形的面积是 ( D )
A.8
B.12
C.18
D.20
2.下列各组线段中,不能构成直角三角形的是 ( C )
A.3,4,5
B.5,12,13
C.8,16,17
D.7,24,25
C
3.若一个三角形的三边长的平方分别为32,42,x2,且此三角形是直角三角形,则x2的值是 ( D )
A.42
B.52
C.7
D.52或7
D
4.如图,这是由两个直角三角形和三个正方形组成的图形,其中两正方形面积分别是S1=22,S2=14,AC=10,则AB= 8 .?
5.如图,在△ABC中,D为BC的中点,AB=5,AD=6,AC=13,试判断AD与AB的位置关系.
解:如图,延长AD到点E,使DE=AD,则AE=2AD=12,连接CE.
因为AD是BC边上的中线,所以CD=BD.又因为AD=DE,∠ADB=∠EDC,所以△ABD≌△ECD.所以CE=AB=5,∠E=∠DAB.
在△ACE中,因为AE2+CE2=52+122=169,AC2=132=169,
所以AE2+CE2=AC2,根据勾股定理的逆定理,可知△ACE是直角三角形,且AC是斜边,所以∠E=90°,于是可得∠DAB=90°.所以AD⊥AB,即AD与AB是垂直关系.
因为AD是BC边上的中线,所以CD=BD.又因为AD=DE,
∠ADB=∠EDC,所以△ABD≌△ECD.所以CE=AB=5,∠E
=∠DAB.
在△ACE中,因为AE2+CE2=52+122=169,AC2=132=169,
所以AE2+CE2=AC2,根据勾股定理的逆定理,可知△ACE是
直角三角形,且AC是斜边,所以∠E=90°,于是可得∠DAB
=90°.所以AD⊥AB,即AD与AB是垂直关系.
第一章 勾股定理
第一章 复习课
1.知道勾股定理及直角三角形的判别条件(即勾股定理的逆定理),会灵活应用它解决简单的几何问题和生活实际问题.
2.能把简单的立体图形转化为平面图形,构造直角三角形求线段长.
◎重点:能运用勾股定理及直角三角形的判别条件解决简单的实际问题.
勾股定理是几何学中一颗璀璨的“明星”,它凝聚了一代又一代数学家的智慧和心血,本节课,我们共同梳理知识点,构建知识网络.
1.直角三角形两直角边的平方和等于斜边的 平方和 ,即对于任意的直角三角形,如果它的两条直角边分别为a、b,斜边为c,那么一定有a2+b2=c2,这就是 勾股定理 .?
2.勾股定理的验证,可以采用测量、数格子、 割补法 ,通过构造 几何图形 ,并计算 图形面积 得出一个等式,从而验证勾股定理.?
3.勾股定理的逆定理是用来判断一个三角形是否是 直角三角形 ,应用时首先确定该三角形的 最长边 ,当 其余两边的平方和等于最长边的平方 时,该三角形才是直角三角形.?
勾股定理的(有关计算)运用
1.现有两根铁棒,它们的长分别为9 cm和12 cm,如果将这两根铁棒作为直角边焊接成一个直角三角形的铁架,那么第三根铁棒的长应为 ( A )
A.15 cm
B.21 cm
C.25 cm
D.无法确定
A
判定是否为直角三角形
2.在下列长度的各组线段中,能组成直角三角形的是 ( C )
A.5 cm,6 cm,7 cm
B.1 cm,4 cm,9 cm
C.5 cm,12 cm,13 cm
D.5 cm,11 cm,12 cm
C
勾股定理解决实际问题
3.如图,飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方4000米处,过了20秒,飞机距离这个男孩头顶5000米.问飞机每小时飞行多少千米?
解:在Rt△ABC中,根据勾股定理可知,
BC2=50002-40002=30002,所以BC=3000米,
3000÷20=150米/秒=540千米/时.
所以飞机每小时飞行540千米.
用于证明两条线段相互垂直
4.如图,在正方形ABCD中,F为DC的中点,E为BC上一点,且EC=????????BC.
?
(1)说明AF与EF的位置关系,并说明理由.
(2)若此正方形的面积是16,求AE的长.
解:(1)如图,连接AE,设EC=a,在正方形ABCD中,因为EC=????????BC,所以BC=4a.所以AD=CD=AB=4a,所以BE=3a.因为F是CD中点,所以DF=CF=2a.
?
在Rt△ABE中,AE2=AB2+BE2=(4a)2+(3a)2=25a2.
同理,在Rt△ADF和Rt△ECF中,AF2=AD2+DF2=(4a)2+(2a)2=20a2,
在Rt△ABE中,AE2=AB2+BE2=(4a)2+(3a)2=25a2.
同理,在Rt△ADF和Rt△ECF中,AF2=AD2+DF2=(4a)2+
(2a)2=20a2,EF2= CE2 +CF2 =a2+(2a)2=5a2,
EF2=5a2,所以AE2=AF2+EF2,所以∠EFA=90°,即AF⊥EF.
(2)因为正方形的面积为16,所以a=1,所以AE2=25a2=25,所以AE=5.
所以AE2=AF2+EF2,所以∠EFA=90°,即
AF⊥EF.
求线段最短问题
5.如图,小河的同一侧有A、B两个小镇,它们到小河所在直线MN的距离分别为BF=2 km,AG=5 km,FG=24 km,要在小河上修建一座小型发电站E,为了节约资源,使得拉到A、B两镇的电线长之和最短,这个电线长之和最短是多少?
解:如图,作点B关于MN的对称点C,并连接AC交MN于点E,连接BE,所以BE+AE=CE+AE=AC.延长AG到D使DG=FC,并连接CD,由已知可知DG=FC=BF=2 km,所以AD=AG+DG=7 km,又因为CD=FG=24 km,在Rt△ADC中,AC2=AD2+CD2=242+72=625,所以AC=25 km,
所以BE+AE=AC=25 km.
1.如图,在△ABC中,∠C=90°,AC=4,BC=2.以AB为一条边向三角形外部作正方形,则正方形的面积是 ( D )
A.8
B.12
C.18
D.20
2.下列各组线段中,不能构成直角三角形的是 ( C )
A.3,4,5
B.5,12,13
C.8,16,17
D.7,24,25
C
3.若一个三角形的三边长的平方分别为32,42,x2,且此三角形是直角三角形,则x2的值是 ( D )
A.42
B.52
C.7
D.52或7
D
4.如图,这是由两个直角三角形和三个正方形组成的图形,其中两正方形面积分别是S1=22,S2=14,AC=10,则AB= 8 .?
5.如图,在△ABC中,D为BC的中点,AB=5,AD=6,AC=13,试判断AD与AB的位置关系.
解:如图,延长AD到点E,使DE=AD,则AE=2AD=12,连接CE.
因为AD是BC边上的中线,所以CD=BD.又因为AD=DE,∠ADB=∠EDC,所以△ABD≌△ECD.所以CE=AB=5,∠E=∠DAB.
在△ACE中,因为AE2+CE2=52+122=169,AC2=132=169,
所以AE2+CE2=AC2,根据勾股定理的逆定理,可知△ACE是直角三角形,且AC是斜边,所以∠E=90°,于是可得∠DAB=90°.所以AD⊥AB,即AD与AB是垂直关系.
因为AD是BC边上的中线,所以CD=BD.又因为AD=DE,
∠ADB=∠EDC,所以△ABD≌△ECD.所以CE=AB=5,∠E
=∠DAB.
在△ACE中,因为AE2+CE2=52+122=169,AC2=132=169,
所以AE2+CE2=AC2,根据勾股定理的逆定理,可知△ACE是
直角三角形,且AC是斜边,所以∠E=90°,于是可得∠DAB
=90°.所以AD⊥AB,即AD与AB是垂直关系.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
