3.1.1椭圆及其标准方程 课件(共29张PPT)
文档属性
| 名称 | 3.1.1椭圆及其标准方程 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
3.1.1 椭圆及其标准方程
生活当中,存在这样一些曲线:
圆锥曲线命名的由来
圆锥曲线的发展历史
阿波罗尼奥斯 (公元前262年-公元前190年,古希腊数学家)
用一个不过圆锥顶点的平面沿不同方向截同一个圆锥,
截出三种不同的圆锥曲线(椭圆、双曲线、抛物线)。
阿波罗尼奥斯在他的经典巨著《圆锥曲线论》中用纯几何方法,证明了近500个命题,将圆锥曲线的性质网罗殆尽,几乎不给后人留有任何研究的余地,堪称希腊几何的最高水平。
圆锥曲线的发展历史
坐 标 法
性质
由形到数
方程
由数到形
数 形 结 合
解析几何基本思想
勒内·笛卡尔 (公元1596年3月31日—公元1650年2月11日)
皮耶·德·费马 (公元1601年8月17日—公元1665年1月12日)
坐标系的发明,解析几何得到创立
椭圆
解析几何基本思想
椭圆
性质
方程
课标
合作探究
2.任务:
①在图纸上确定两点F1、F2;
②请合作将桌上细绳两端固定在F1、F2处;
③用铅笔尖(M)把细绳拉紧,在板上慢慢移动并观察画出的图形.
1.要求:请奇数排同学后转,前后两排四位同学一组,合作探究;
探究一:(三分钟)
课标
合作探究
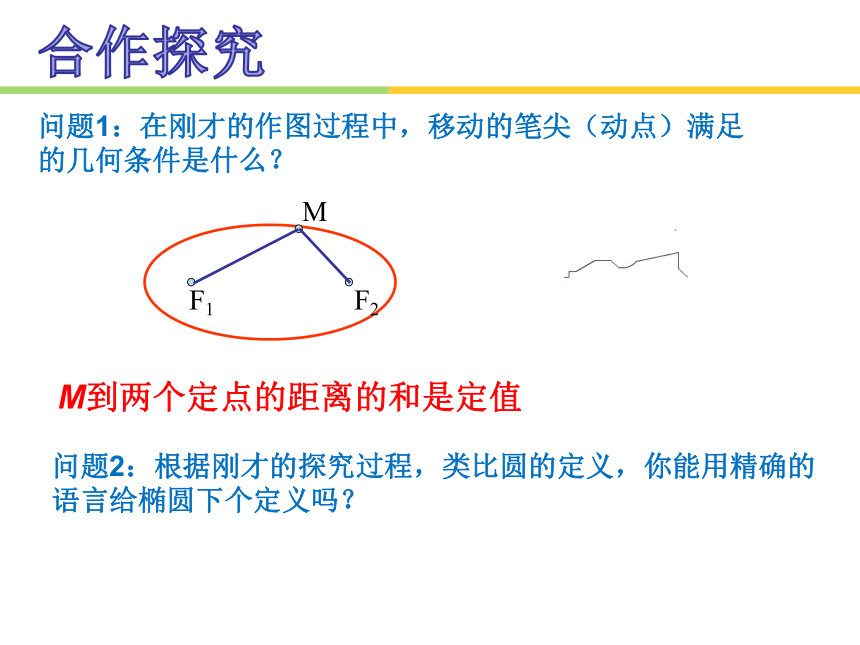
问题1:在刚才的作图过程中,移动的笔尖(动点)满足的几何条件是什么?
M到两个定点的距离的和是定值
问题2:根据刚才的探究过程,类比圆的定义,你能用精确的语言给椭圆下个定义吗?
F1
F2
M
课标
椭圆的定义
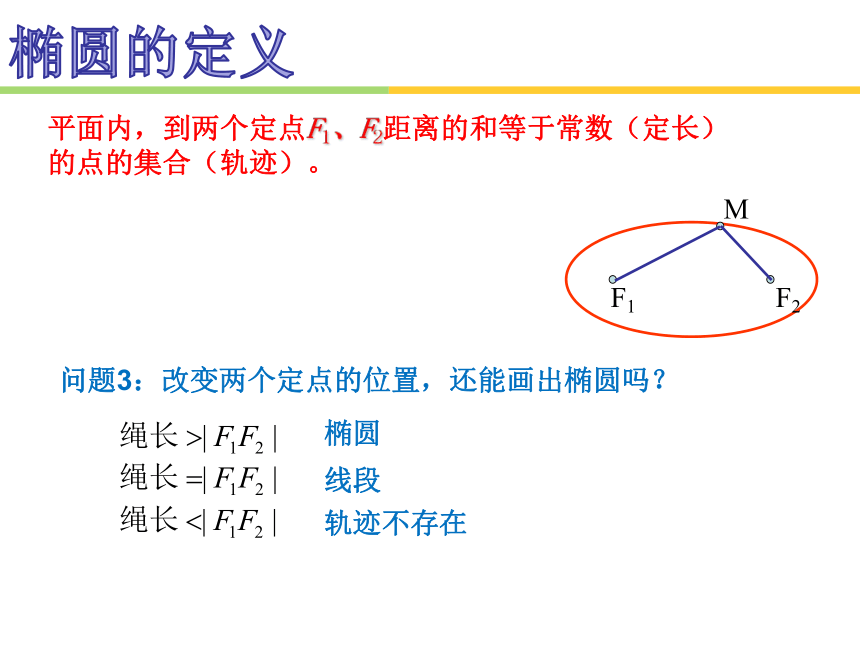
平面内,到两个定点F1、F2距离的和等于常数(定长)
的点的集合(轨迹)。
F1
F2
M
问题3:改变两个定点的位置,还能画出椭圆吗?
椭圆
线段
轨迹不存在
课标
F1
F2
M
椭圆的定义
平面内,与两个定点F1、F2的距离的和等于常数
的点的轨迹。
定点F1、F2叫做椭圆的焦点,
两焦点距离|F1F2|叫做椭圆的焦距
(大于|F1F2 |)
符号语言:
椭圆上点
的集合为
椭圆
线段
轨迹不存在
课标
椭圆的方程
问题4:用坐标法求曲线方程的一般步骤是什么?
建系
设点
列式
化简
检验
F1
F2
M
以刚才的小组为单位,交流建系方式,并在图纸上建立直角坐标系.
探究二:
课标
F1
F2
M
椭圆的方程
F1
F2
M
(1)建系:
对称、简洁
课标
椭圆的方程
(1)建系:
F1
F2
M
以F1、F2所在直线为x轴,线段F1F2 垂直平分线为y轴,建立平面直角坐标系
(2)设点:
设M(x,y)是椭圆上任意一点,
|F1F2|=2c(c>0),
则F1(-c,0)、F2(c,0)
设点M到F1 、F2距离和为2
(3)列式:
由椭圆定义,
建系
设点
列式
化简
检验
课标
椭圆的方程
(4)化简:
方法一:直接平方
课标
椭圆的方程
(4)化简:
移项得
平方得
整理得
平方得
整理得
两边同时除以 ,得
方法二:移项平方
怎样更简洁呢?
课标
椭圆的方程
方法三:
方法四:
两式平方作差
课标
椭圆的方程
(5)检验:
椭圆上点的坐标都符合方程;反之,以方程的解为坐标的点都在椭圆上.
问题5:观察右图,你能从中找出表
示 的线段吗?
课标
椭圆的方程
课标
F1
F2
M
x
O
y
F1
F2
M
O
x
椭圆的标准方程
焦点在 x 轴上,
焦点在 y 轴上,
课标
椭圆的定义 图形
标准方程
焦点坐标
关系
F1
F2
M
x
O
y
F1
F2
M
O
x
椭圆的标准方程
课标
典例探究
焦点位置
看分母大小
课标
典例探究
定位
定量
定义法
课标
典例探究
定位
定量
待定系数法
课标
小结提升
课标
课后作业
问题6:倾斜水杯中液面与杯身形成的截口曲线、手电筒照射下乒乓球的影子是椭圆吗?
课标
课后作业
19世纪,法国数学家旦德林就想到了一种绝妙的方法:
旦德林双球模型
课标
课后作业
一.基础性作业:
1.复习回顾椭圆标准方程的推导过程;
2.完成课本第109页1,2,3题.
三.拓展性作业:
查阅资料,了解旦德林双球模型的有关知识,撰写小论文.
二.提升性作业:
探究椭圆标准方程的其他推导方法;
强国有我!
从1970年4月24日,
长征一号成功发射,
50年间,
我国航天事业实现了跨越式
发展,
取得了举世瞩目的成就,
从航天大国迈向航天强国!
椭圆(知识、能力)
自立自强、为国奋斗
科学、严谨、精益求精
强国有我!
课标
谢谢!
3.1.1 椭圆及其标准方程
生活当中,存在这样一些曲线:
圆锥曲线命名的由来
圆锥曲线的发展历史
阿波罗尼奥斯 (公元前262年-公元前190年,古希腊数学家)
用一个不过圆锥顶点的平面沿不同方向截同一个圆锥,
截出三种不同的圆锥曲线(椭圆、双曲线、抛物线)。
阿波罗尼奥斯在他的经典巨著《圆锥曲线论》中用纯几何方法,证明了近500个命题,将圆锥曲线的性质网罗殆尽,几乎不给后人留有任何研究的余地,堪称希腊几何的最高水平。
圆锥曲线的发展历史
坐 标 法
性质
由形到数
方程
由数到形
数 形 结 合
解析几何基本思想
勒内·笛卡尔 (公元1596年3月31日—公元1650年2月11日)
皮耶·德·费马 (公元1601年8月17日—公元1665年1月12日)
坐标系的发明,解析几何得到创立
椭圆
解析几何基本思想
椭圆
性质
方程
课标
合作探究
2.任务:
①在图纸上确定两点F1、F2;
②请合作将桌上细绳两端固定在F1、F2处;
③用铅笔尖(M)把细绳拉紧,在板上慢慢移动并观察画出的图形.
1.要求:请奇数排同学后转,前后两排四位同学一组,合作探究;
探究一:(三分钟)
课标
合作探究
问题1:在刚才的作图过程中,移动的笔尖(动点)满足的几何条件是什么?
M到两个定点的距离的和是定值
问题2:根据刚才的探究过程,类比圆的定义,你能用精确的语言给椭圆下个定义吗?
F1
F2
M
课标
椭圆的定义
平面内,到两个定点F1、F2距离的和等于常数(定长)
的点的集合(轨迹)。
F1
F2
M
问题3:改变两个定点的位置,还能画出椭圆吗?
椭圆
线段
轨迹不存在
课标
F1
F2
M
椭圆的定义
平面内,与两个定点F1、F2的距离的和等于常数
的点的轨迹。
定点F1、F2叫做椭圆的焦点,
两焦点距离|F1F2|叫做椭圆的焦距
(大于|F1F2 |)
符号语言:
椭圆上点
的集合为
椭圆
线段
轨迹不存在
课标
椭圆的方程
问题4:用坐标法求曲线方程的一般步骤是什么?
建系
设点
列式
化简
检验
F1
F2
M
以刚才的小组为单位,交流建系方式,并在图纸上建立直角坐标系.
探究二:
课标
F1
F2
M
椭圆的方程
F1
F2
M
(1)建系:
对称、简洁
课标
椭圆的方程
(1)建系:
F1
F2
M
以F1、F2所在直线为x轴,线段F1F2 垂直平分线为y轴,建立平面直角坐标系
(2)设点:
设M(x,y)是椭圆上任意一点,
|F1F2|=2c(c>0),
则F1(-c,0)、F2(c,0)
设点M到F1 、F2距离和为2
(3)列式:
由椭圆定义,
建系
设点
列式
化简
检验
课标
椭圆的方程
(4)化简:
方法一:直接平方
课标
椭圆的方程
(4)化简:
移项得
平方得
整理得
平方得
整理得
两边同时除以 ,得
方法二:移项平方
怎样更简洁呢?
课标
椭圆的方程
方法三:
方法四:
两式平方作差
课标
椭圆的方程
(5)检验:
椭圆上点的坐标都符合方程;反之,以方程的解为坐标的点都在椭圆上.
问题5:观察右图,你能从中找出表
示 的线段吗?
课标
椭圆的方程
课标
F1
F2
M
x
O
y
F1
F2
M
O
x
椭圆的标准方程
焦点在 x 轴上,
焦点在 y 轴上,
课标
椭圆的定义 图形
标准方程
焦点坐标
关系
F1
F2
M
x
O
y
F1
F2
M
O
x
椭圆的标准方程
课标
典例探究
焦点位置
看分母大小
课标
典例探究
定位
定量
定义法
课标
典例探究
定位
定量
待定系数法
课标
小结提升
课标
课后作业
问题6:倾斜水杯中液面与杯身形成的截口曲线、手电筒照射下乒乓球的影子是椭圆吗?
课标
课后作业
19世纪,法国数学家旦德林就想到了一种绝妙的方法:
旦德林双球模型
课标
课后作业
一.基础性作业:
1.复习回顾椭圆标准方程的推导过程;
2.完成课本第109页1,2,3题.
三.拓展性作业:
查阅资料,了解旦德林双球模型的有关知识,撰写小论文.
二.提升性作业:
探究椭圆标准方程的其他推导方法;
强国有我!
从1970年4月24日,
长征一号成功发射,
50年间,
我国航天事业实现了跨越式
发展,
取得了举世瞩目的成就,
从航天大国迈向航天强国!
椭圆(知识、能力)
自立自强、为国奋斗
科学、严谨、精益求精
强国有我!
课标
谢谢!
