人教版七年级数学上册第四章《几何图形初步》单元练习题(含答案)
文档属性
| 名称 | 人教版七年级数学上册第四章《几何图形初步》单元练习题(含答案) | 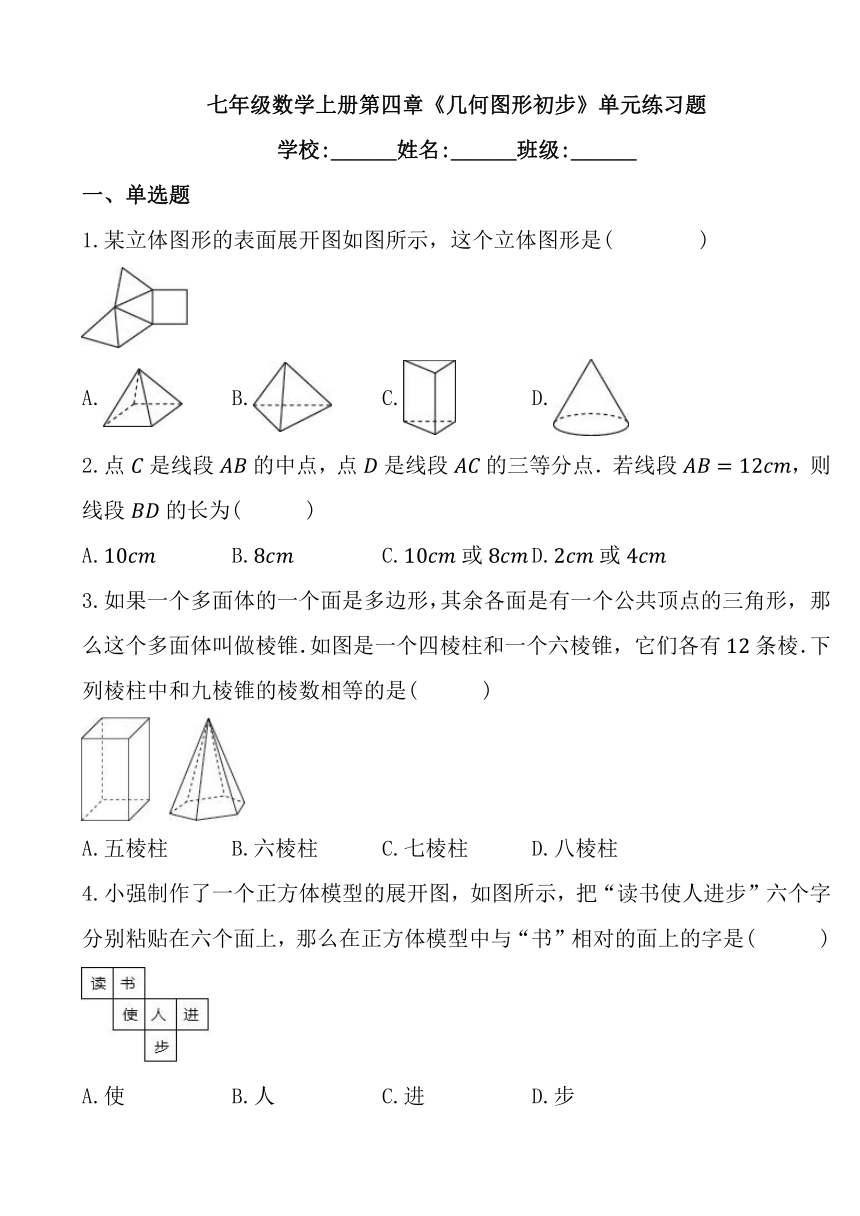 | |
| 格式 | docx | ||
| 文件大小 | 114.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 19:13:13 | ||
图片预览




文档简介
七年级数学上册第四章《几何图形初步》单元练习题
学校:______姓名:______班级:______
一、单选题
1.某立体图形的表面展开图如图所示,这个立体图形是( )
A. B. C. D.
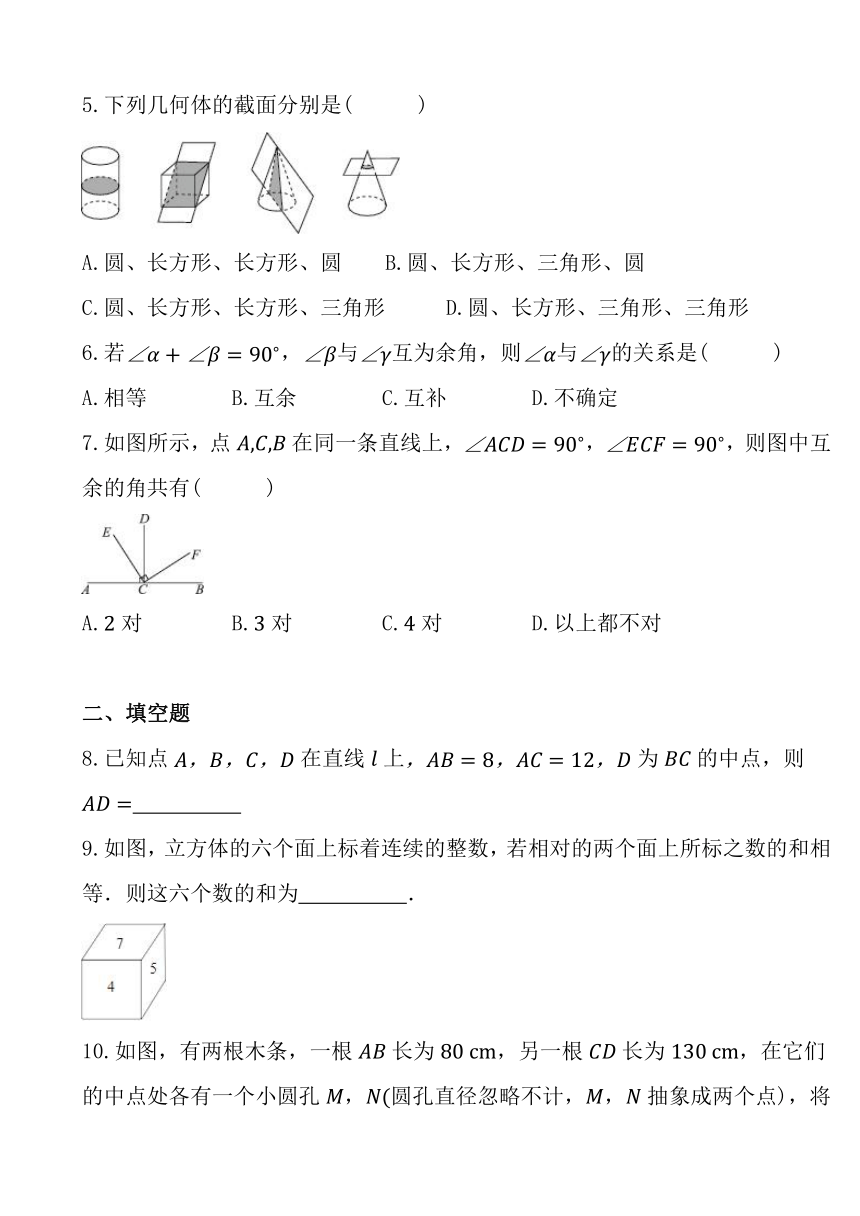
2.点是线段的中点,点是线段的三等分点.若线段,则线段的长为( )
A. B. C.或 D.或
3.如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形, 那么这个多面体叫做棱锥.如图是一个四棱柱和一个六棱锥, 它们各有条棱.下列棱柱中和九棱锥的棱数相等的是( )
A.五棱柱 B.六棱柱 C.七棱柱 D.八棱柱
4.小强制作了一个正方体模型的展开图,如图所示,把“读书使人进步”六个字分别粘贴在六个面上,那么在正方体模型中与“书”相对的面上的字是( )
A.使 B.人 C.进 D.步
5.下列几何体的截面分别是( )
A.圆、长方形、长方形、圆 B.圆、长方形、三角形、圆
C.圆、长方形、长方形、三角形 D.圆、长方形、三角形、三角形
6.若,与互为余角,则与的关系是( )
A.相等 B.互余 C.互补 D.不确定
7.如图所示,点在同一条直线上,,,则图中互余的角共有( )
A.对 B.对 C.对 D.以上都不对
二、填空题
8.已知点在直线上为的中点,则
9.如图,立方体的六个面上标着连续的整数,若相对的两个面上所标之数的和相等.则这六个数的和为 .
10.如图,有两根木条,一根长为,另一根长为,在它们的中点处各有一个小圆孔,圆孔直径忽略不计,,抽象成两个点),将它们的一端重合,放置在同一条直线上,则此时两根木条的小圆孔之间的距离 .
11.已知一条射线,若从点再引两条射线和,使,,若平分,则的度数为 .
12.如图所示,已知,,平分,平分,则的度数为 .
13.如图,是的平分线,是内的一条射线.已知比大,则的度数是 .
14.如图是一个时钟的钟面,下午点分,时钟的分针与时针所夹的角等于 .
15.已知α与β互余,且α′,则β .
16.如图,将三个边长相同的正方形的一个顶点重合放置,已知,,则 度.
三、解答题
17.作图题:已知线段,,射线.
(1)尺规作图:在射线上截取,且(保留作图痕迹,不写作法);
(2)在的图中,标出的中点,的三等分点左右),并用含,的式子表示线段的长.
18.如图,已知点,在线段上.
(1)图中共有 条线段;
(2)若,,是的中点,是的中点,求的长度.
19.如图,直线与相交于点.
(1)如图①,若平分,求的度数;
(2)如图②,若,且平分,求的度数.
20.一个角的余角比它的补角的还少,求这个角的度数.
21.在飞机飞行时,飞行方向是用飞行路线与实际的南或北方向线之间的夹角大小来表示的,如图,用南北线)与飞行线之间顺时针方向的夹角作为飞行方向角,从到的飞行方向角为,从到的飞行方向角为,从到的飞行方向角为,问:与之间的夹角为多少度?与之间的夹角为多少度?并画出从飞出且方向角为的飞行线.
22.如图,将两块直角三角板的直角顶点叠放在一起.
(1)猜想与的大小关系,并说明理由;
(2)求的度数;
(3)若与的度数比为∶,求的度数.
参考答案
1.A
2.C
3.B
4.D
5.B
6.A
7.C
8.或
9.
10.或
11.或
12.
13.
14.
15.′
16.
17.(1)解:如图.
(2)标出点,,.如图:根据题意得,所以.
18.(1)
(2)解:因为,,所以.因为是的中点,是的中点,所以,,所以,所以.因此,的长度是.
19.(1)解:,平分,
,
,,
即的度数为.
(2)因为平分,所以设.
因为,所以,
所以.
因为,
所以,
解得.
故.
20.解:设这个角的度数为,那么这个角的余角的度数为,它的补角的度数为.
根据题意列方程,得,
解得,
所以这个角的度数为.
21.解:由题意可知,,.
故与之间的夹角为,
与之间的夹角为.
如图:
22.(1).理由如下: 因为, 所以同角的余角相等)
(2)
(3)设,那么, 故, 所以,解得, 故,
学校:______姓名:______班级:______
一、单选题
1.某立体图形的表面展开图如图所示,这个立体图形是( )
A. B. C. D.
2.点是线段的中点,点是线段的三等分点.若线段,则线段的长为( )
A. B. C.或 D.或
3.如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形, 那么这个多面体叫做棱锥.如图是一个四棱柱和一个六棱锥, 它们各有条棱.下列棱柱中和九棱锥的棱数相等的是( )
A.五棱柱 B.六棱柱 C.七棱柱 D.八棱柱
4.小强制作了一个正方体模型的展开图,如图所示,把“读书使人进步”六个字分别粘贴在六个面上,那么在正方体模型中与“书”相对的面上的字是( )
A.使 B.人 C.进 D.步
5.下列几何体的截面分别是( )
A.圆、长方形、长方形、圆 B.圆、长方形、三角形、圆
C.圆、长方形、长方形、三角形 D.圆、长方形、三角形、三角形
6.若,与互为余角,则与的关系是( )
A.相等 B.互余 C.互补 D.不确定
7.如图所示,点在同一条直线上,,,则图中互余的角共有( )
A.对 B.对 C.对 D.以上都不对
二、填空题
8.已知点在直线上为的中点,则
9.如图,立方体的六个面上标着连续的整数,若相对的两个面上所标之数的和相等.则这六个数的和为 .
10.如图,有两根木条,一根长为,另一根长为,在它们的中点处各有一个小圆孔,圆孔直径忽略不计,,抽象成两个点),将它们的一端重合,放置在同一条直线上,则此时两根木条的小圆孔之间的距离 .
11.已知一条射线,若从点再引两条射线和,使,,若平分,则的度数为 .
12.如图所示,已知,,平分,平分,则的度数为 .
13.如图,是的平分线,是内的一条射线.已知比大,则的度数是 .
14.如图是一个时钟的钟面,下午点分,时钟的分针与时针所夹的角等于 .
15.已知α与β互余,且α′,则β .
16.如图,将三个边长相同的正方形的一个顶点重合放置,已知,,则 度.
三、解答题
17.作图题:已知线段,,射线.
(1)尺规作图:在射线上截取,且(保留作图痕迹,不写作法);
(2)在的图中,标出的中点,的三等分点左右),并用含,的式子表示线段的长.
18.如图,已知点,在线段上.
(1)图中共有 条线段;
(2)若,,是的中点,是的中点,求的长度.
19.如图,直线与相交于点.
(1)如图①,若平分,求的度数;
(2)如图②,若,且平分,求的度数.
20.一个角的余角比它的补角的还少,求这个角的度数.
21.在飞机飞行时,飞行方向是用飞行路线与实际的南或北方向线之间的夹角大小来表示的,如图,用南北线)与飞行线之间顺时针方向的夹角作为飞行方向角,从到的飞行方向角为,从到的飞行方向角为,从到的飞行方向角为,问:与之间的夹角为多少度?与之间的夹角为多少度?并画出从飞出且方向角为的飞行线.
22.如图,将两块直角三角板的直角顶点叠放在一起.
(1)猜想与的大小关系,并说明理由;
(2)求的度数;
(3)若与的度数比为∶,求的度数.
参考答案
1.A
2.C
3.B
4.D
5.B
6.A
7.C
8.或
9.
10.或
11.或
12.
13.
14.
15.′
16.
17.(1)解:如图.
(2)标出点,,.如图:根据题意得,所以.
18.(1)
(2)解:因为,,所以.因为是的中点,是的中点,所以,,所以,所以.因此,的长度是.
19.(1)解:,平分,
,
,,
即的度数为.
(2)因为平分,所以设.
因为,所以,
所以.
因为,
所以,
解得.
故.
20.解:设这个角的度数为,那么这个角的余角的度数为,它的补角的度数为.
根据题意列方程,得,
解得,
所以这个角的度数为.
21.解:由题意可知,,.
故与之间的夹角为,
与之间的夹角为.
如图:
22.(1).理由如下: 因为, 所以同角的余角相等)
(2)
(3)设,那么, 故, 所以,解得, 故,
