5.1.2弧度制 课件(共18张PPT)
文档属性
| 名称 | 5.1.2弧度制 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 387.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 09:40:59 | ||
图片预览





文档简介
(共18张PPT)
5.1.2 弧度制
为了认清事情的本质,人类创造了很多工具,数学就是其中之一,为解决问题的方便,便创造了许多各种各样的单位制。
如:长度单位(千米、米、厘米、毫米......)
约在公元2000年,古巴比伦人创设性地将圆周划分为360度,每度为60分,每分再划分为60秒。
角度制
2、这种用度作为单位来度量角的单位制叫做角度制。
1、规定周角的 为1度的角。
如何计算30 +sin30 =?
问题情景
某地区为宣扬社会主义核心价值观需要生产和图中一样的扇形广告宣传牌,技术人员需要计算一下扇形的面积,用来测算需要的原材料的量,若他手中只有一把钢卷尺,能用现有的工具测算出扇形的大致面积吗?
合作探究
器材:扇形教具、绳子、直尺
要求:请同学们相互协作,用手中的工具测量扇形的圆心角。
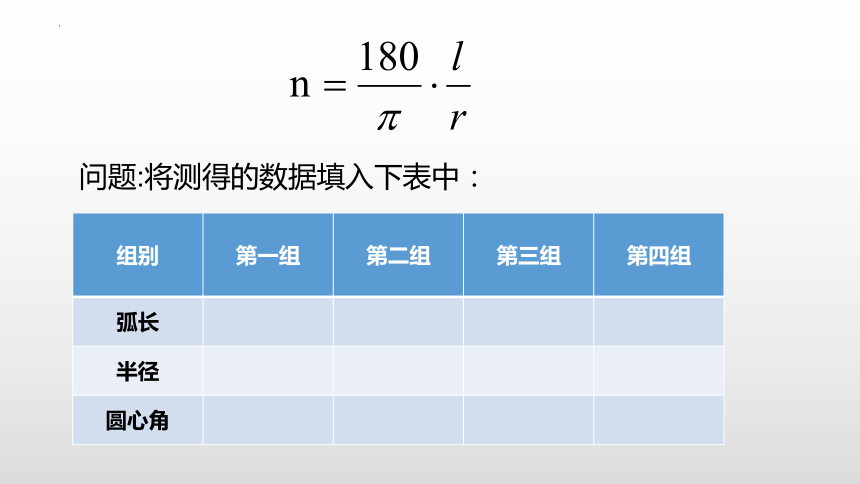
问题:将测得的数据填入下表中:
组别 第一组 第二组 第三组
第四组
弧长
半径
圆心角
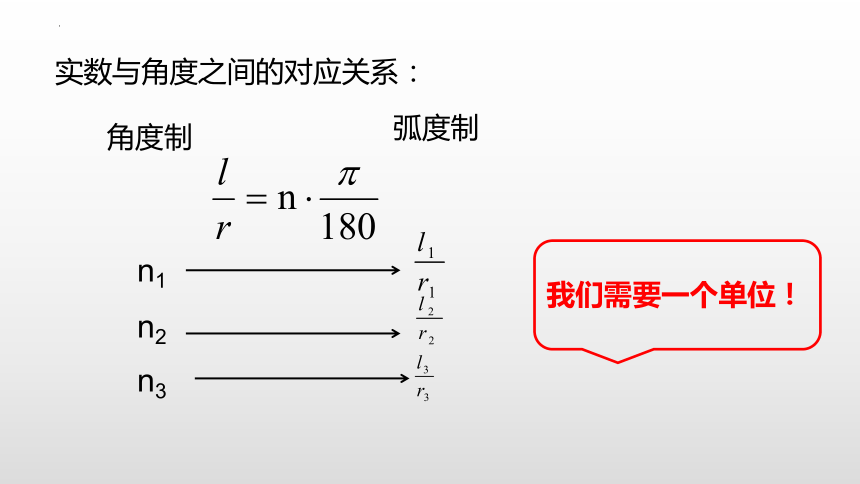
实数与角度之间的对应关系:
角度制
弧度制
n2
n1
n3
我们需要一个单位!
一、弧度制
我们把长度等于半径长的弧所对的圆心角叫做1弧度的角。“弧度”常用“rad”表示。
1弧度
r
l=r
O
A
B
2 rad
3 rad
2 π rad
设弧AB的长为l :
若l=2r,则∠AOB=
若l=3r,则∠AOB=
若l=2πr,则∠AOB=
练一练:
问题:弧度制是否可以度量任意角?
其中,α的正负由旋转方向决定,逆时针为正,顺时针为负,当角的终边旋转一周后继续旋转,就可以得到大于2π或小于0的角,这样就可以得到弧度为任意大小的角。
在半径为r的圆中,弧长为 的弧所对的圆心角为αrad,则:
︱α︱=
r
弧度制的发展
1,公元6世纪,印度人在制作正弦表时,曾用同一单位度量半径和圆周,孕育着最早的弧度制的概念。
2,1748年瑞士数学家欧拉出版的一部划时代的著作《无穷小分析概论》中,明确提出把圆的半径作为弧长的度量单位,将线段与弧的度量统一起来,大大的简化了三角公式及计算。
萌芽阶段
传播阶段
确立阶段
公元前300年
公元640年
15世纪文艺复兴前
至今三角学发展
二、弧度与角度的换算
360°= 2π 弧度
180°= π 弧度
l=2 π r
O
(B)
r
1°= —— 弧度 ≈ 0.01745 弧度
180
π
1弧度 =(——)°≈ 57.30°= 57°18′
π
180
三、例题
例1(1) 把 67°30′化成弧度。
(2) 把 — π 弧度化成度。
5
3
解:
解:
1°= —— 弧度
180
π
1弧度 =(——)°
π
180
请写出一些特殊角的弧度数
四、练习:
注: 1.用弧度为单位表示角的大小时, “弧度”二字或“rad”
通常省略不写,但用“度”(°)为单位不能省。
2.用弧度为单位表示角时,通常写 成“多少π”的形式,
如无特别要求,不用将π化成小数。
度 0 30 45 60 90 120 135 150 180 270 360
弧度数
例2:利用弧度制证明下列关于扇形的公式:
(1) = αR
(2)S = αR2
(3)S = R
R是圆的半径,α为圆心角, 是扇形的弧长,S是扇形的面积.
情景再现
某地区为宣扬社会主义核心价值观需要生产和图中一样的扇形广告宣传牌,技术人员需要计算一下扇形的面积,用来测算需要的原材料的量,若他手中只有一把钢卷尺,能用现有的工具测算出扇形的大致面积吗?
S = R
弧度制的意义
(1)“通”:使单位制统一
(2)“简”:简化公式
当堂检测:
1.把下列角度化成弧度.
2.把下列弧度化成角度.
(2)
3.用弧度制表示终边在x轴上的角的集合
(1)22 30' -210 1200
弧度制 角度制
度量单位 弧度(10进制) 度(60进制,1 =60,1′=60 )
单位规定 把长度等于半径长的弧所对的圆心角叫做1弧度的角。 周角的1/360叫做1度的角。
换算关系
基本关系
导出关系
五、小结:
5.1.2 弧度制
为了认清事情的本质,人类创造了很多工具,数学就是其中之一,为解决问题的方便,便创造了许多各种各样的单位制。
如:长度单位(千米、米、厘米、毫米......)
约在公元2000年,古巴比伦人创设性地将圆周划分为360度,每度为60分,每分再划分为60秒。
角度制
2、这种用度作为单位来度量角的单位制叫做角度制。
1、规定周角的 为1度的角。
如何计算30 +sin30 =?
问题情景
某地区为宣扬社会主义核心价值观需要生产和图中一样的扇形广告宣传牌,技术人员需要计算一下扇形的面积,用来测算需要的原材料的量,若他手中只有一把钢卷尺,能用现有的工具测算出扇形的大致面积吗?
合作探究
器材:扇形教具、绳子、直尺
要求:请同学们相互协作,用手中的工具测量扇形的圆心角。
问题:将测得的数据填入下表中:
组别 第一组 第二组 第三组
第四组
弧长
半径
圆心角
实数与角度之间的对应关系:
角度制
弧度制
n2
n1
n3
我们需要一个单位!
一、弧度制
我们把长度等于半径长的弧所对的圆心角叫做1弧度的角。“弧度”常用“rad”表示。
1弧度
r
l=r
O
A
B
2 rad
3 rad
2 π rad
设弧AB的长为l :
若l=2r,则∠AOB=
若l=3r,则∠AOB=
若l=2πr,则∠AOB=
练一练:
问题:弧度制是否可以度量任意角?
其中,α的正负由旋转方向决定,逆时针为正,顺时针为负,当角的终边旋转一周后继续旋转,就可以得到大于2π或小于0的角,这样就可以得到弧度为任意大小的角。
在半径为r的圆中,弧长为 的弧所对的圆心角为αrad,则:
︱α︱=
r
弧度制的发展
1,公元6世纪,印度人在制作正弦表时,曾用同一单位度量半径和圆周,孕育着最早的弧度制的概念。
2,1748年瑞士数学家欧拉出版的一部划时代的著作《无穷小分析概论》中,明确提出把圆的半径作为弧长的度量单位,将线段与弧的度量统一起来,大大的简化了三角公式及计算。
萌芽阶段
传播阶段
确立阶段
公元前300年
公元640年
15世纪文艺复兴前
至今三角学发展
二、弧度与角度的换算
360°= 2π 弧度
180°= π 弧度
l=2 π r
O
(B)
r
1°= —— 弧度 ≈ 0.01745 弧度
180
π
1弧度 =(——)°≈ 57.30°= 57°18′
π
180
三、例题
例1(1) 把 67°30′化成弧度。
(2) 把 — π 弧度化成度。
5
3
解:
解:
1°= —— 弧度
180
π
1弧度 =(——)°
π
180
请写出一些特殊角的弧度数
四、练习:
注: 1.用弧度为单位表示角的大小时, “弧度”二字或“rad”
通常省略不写,但用“度”(°)为单位不能省。
2.用弧度为单位表示角时,通常写 成“多少π”的形式,
如无特别要求,不用将π化成小数。
度 0 30 45 60 90 120 135 150 180 270 360
弧度数
例2:利用弧度制证明下列关于扇形的公式:
(1) = αR
(2)S = αR2
(3)S = R
R是圆的半径,α为圆心角, 是扇形的弧长,S是扇形的面积.
情景再现
某地区为宣扬社会主义核心价值观需要生产和图中一样的扇形广告宣传牌,技术人员需要计算一下扇形的面积,用来测算需要的原材料的量,若他手中只有一把钢卷尺,能用现有的工具测算出扇形的大致面积吗?
S = R
弧度制的意义
(1)“通”:使单位制统一
(2)“简”:简化公式
当堂检测:
1.把下列角度化成弧度.
2.把下列弧度化成角度.
(2)
3.用弧度制表示终边在x轴上的角的集合
(1)22 30' -210 1200
弧度制 角度制
度量单位 弧度(10进制) 度(60进制,1 =60,1′=60 )
单位规定 把长度等于半径长的弧所对的圆心角叫做1弧度的角。 周角的1/360叫做1度的角。
换算关系
基本关系
导出关系
五、小结:
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
