数学人教A版(2019)必修第一册4.2.1指数函数的概念(共21张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.2.1指数函数的概念(共21张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
4.2.1 指数函数的概念
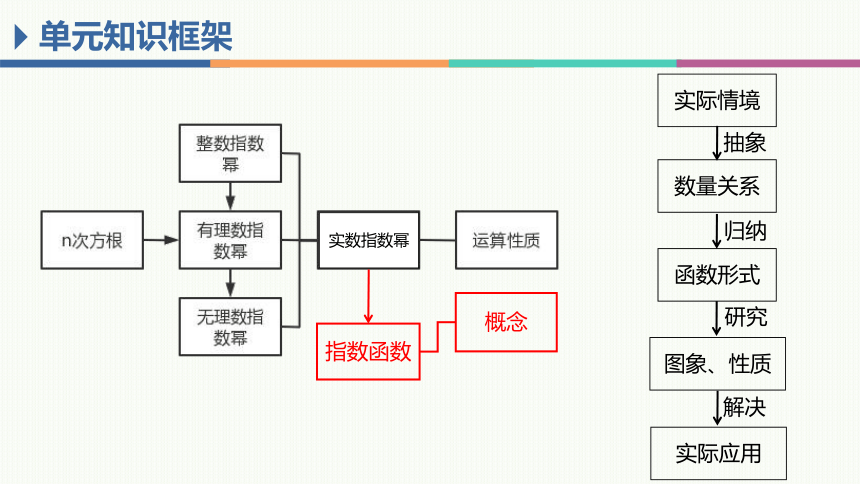
单元知识框架
实际情境
数量关系
抽象
函数形式
归纳
图象、性质
研究
实际应用
解决
概念
指数函数
实数指数幂
学习目标
二.学习重点与难点
重点:指数函数的概念
难点:概括指数函数概念的过程,对指数函数的理解
一.学习目标
(1)通过具体实例,了解指数函数的实际意义,理解指数函数的概念.
(2)体会指数函数概念的形成过程,提升数学抽象、逻辑推理和数学建 模核心素养.
新知探究
问题1 随着中国经济高速增长,人民生活水平不断提高,旅游成了越来越多家庭的重要生活方式.由于旅游人数不断增加,A,B两地景区自2001年起采取了不同的应对措施:
A地提高了景区门票价格,
而B地则取消了景区门票.
下表给出了A,B两地景区2001年至2015年的游客人次以及逐年增加量.
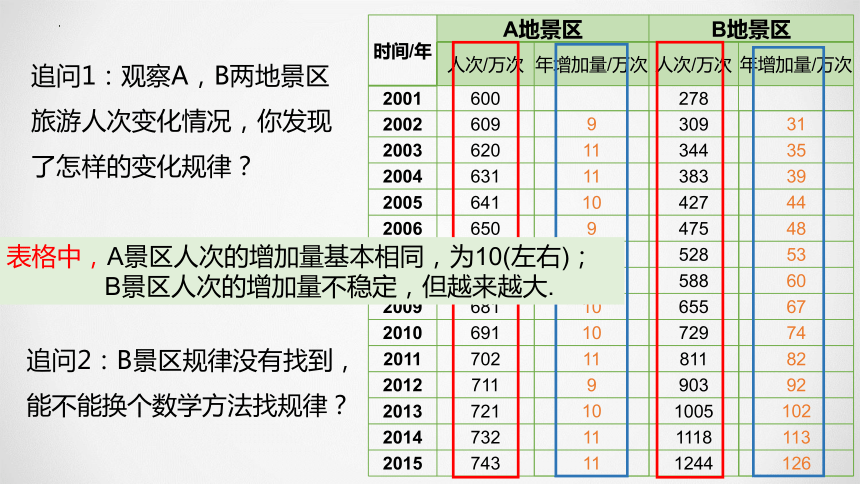
比较两地景区游客人次的变化情况.你发现了怎样的变化规律?
时间/年A地景区B地景区人次/万次年增加量/万次人次/万次年增加量/万次2001600 278 2002609309200362034420046313832005641427200665047520076615282008671588200968165520106917292011702811201271190320137211005201473211182015743124491111109111010101191011113135394448536067748292102113126追问1:观察A,B两地景区旅游人次变化情况,你发现了怎样的变化规律?追问2:B景区规律没有找到,能不能换个数学方法找规律?表格中,A景区人次的增加量基本相同,为10(左右);B景区人次的增加量不稳定,但越来越大.A地景区 时间/年 人次/万次
2001 600
2002 609
2003 620
2004 631
2005 641
2006 650
2007 661
2008 671
2009 681
2010 691
2011 702
2012 711
2013 721
2014 732
2015 743
B地景区 时间/年 人次/万次
2001 278
2002 309
2003 344
2004 383
2005 427
2006 475
2007 528
2008 588
2009 655
2010 729
2011 811
2012 903
2013 1005
2014 1118
2015 1244
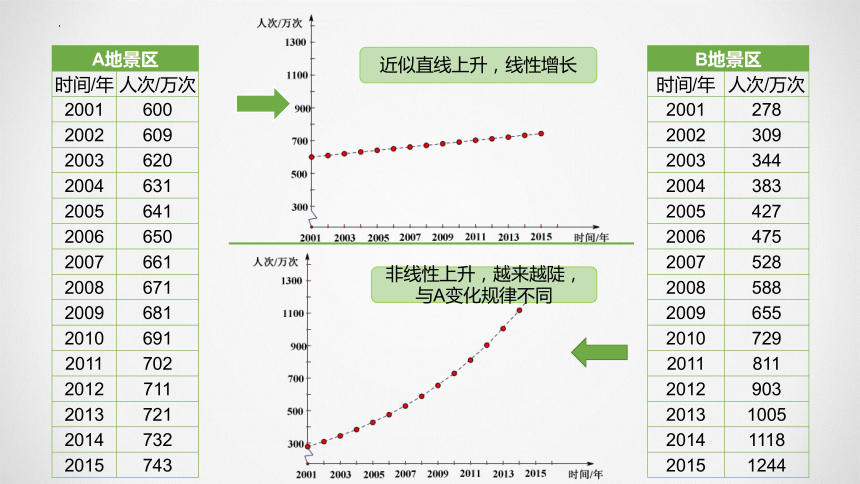
近似直线上升,线性增长
非线性上升,越来越陡,
与A变化规律不同
B地景区 时间/年 人次/万次
2001 278
2002 309
2003 344
2004 383
2005 427
2006 475
2007 528
2008 588
2009 655
2010 729
2011 811
2012 903
2013 1005
2014 1118
2015 1244
…………
追问3:代数运算是寻找变化规律的基本方法.A地变化规律通过哪个不变量找到的?B地景区游客人次是否也可以用如类似这样的不变量来刻画呢?
试计算游客人次的年增长率
像这样,增长率为常数的变化方式,我们称为指数增长.
B地景区的游客人次的年增长率都约为
是一个常数.
1年后,游客人次是2001年的___________倍;
2年后,游客人次是2001年的___________倍;
3年后,游客人次是2001年的___________倍;
……
年后,游客人次是2001年的___________倍.
从2001年开始,B地景区游客人次的变化规律可以近似描述为:
如果设经过 年后的游客人次为2001年的 倍,
那么 =______________________
这是一个函数,其中指数 是自变量.
自变量增加1个单位,
小结:函数变化规律为:
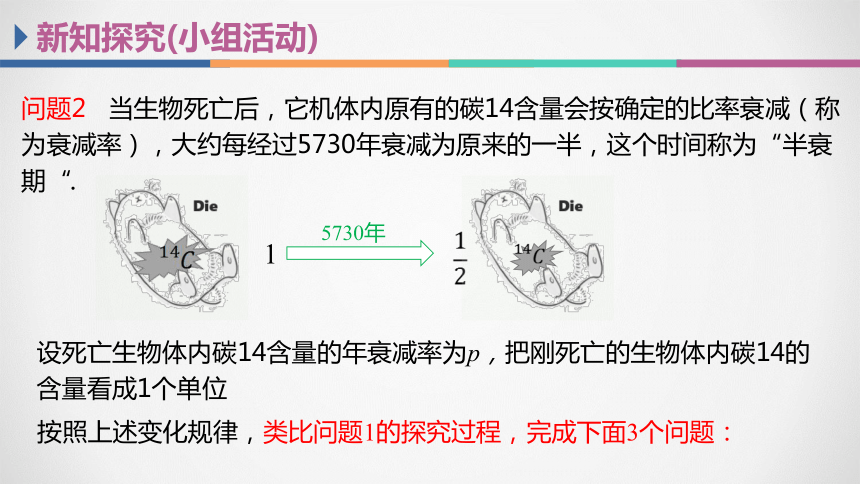
新知探究(小组活动)
问题2 当生物死亡后,它机体内原有的碳14含量会按确定的比率衰减(称为衰减率),大约每经过5730年衰减为原来的一半,这个时间称为“半衰期“.
5730年
1
设死亡生物体内碳14含量的年衰减率为p,把刚死亡的生物体内碳14的含量看成1个单位
按照上述变化规律,类比问题1的探究过程,完成下面3个问题:
像这样,衰减率为常数的变化方式,我们称为指数衰减.
追问1:按规律,填写表格
死亡年数x
1年
2年
3年
······
5730年
年
碳14含量y
追问2:生物体内碳14含量y与死亡年数x之间有怎样的关系?
追问3:求出生物死亡后体内碳14含量年衰减率 的值.
小结:函数变化规律为:
自变量增加1个单位,
则:y与x的函数关系为:
概念抽象
问题:以上函数的解析式有何共同特征?能否用一个式子来反映这些特征?
一般地,函数 叫做指数函数,其中指数x是自变量,定义域是R.
指数
指数
指数
常数
常数
常数
幂
幂
幂
自变量的位置
底数
形式
函数解析式
新知应用
例1 已知函数
(1)求函数 的解析式;
(2)求 的值.
新知应用
例2 (1)在问题1中,平均每位游客出游一次可给当地带来1000元门票之外的收入,A地景区的门票价格为150元,比较这15年间A,B两地旅游收入变化情况.
前情提要:A地景区2001年旅游人次600万,年增加量10万人次;
B地景区2001年旅游人次278万,年增长率0.11.
(1)建立经过x年,游客给A,B两地带来的旅游收入的函数f(x)和g(x).
(2)如何比较 f(x)和g(x)大小?
(3)通过图象之间的关系,描述15年间A,B两地景区的收入变化情况.
思路分析:
新知应用
把形如 的函数称为指数型函数.
指数增长模型:设原有量为 ,每次的增长率为 则经过 次增长,该量增长到 则
指数衰减模型:设原有量为 ,每次的衰减率为 则经过 次衰减,该量减少到 则
指数增长
指数衰减
( N, )
( N, )
课堂练习
解:设核电站爆炸时锶90最初的量为
依题意,经过 年后,锶90的量变为
所以,800年后原有的锶90还剩
1986年4月26日,乌克兰境内的切尔诺贝利核电站爆炸,核泄漏导致事故所在地被严重污染.主要的核污染物是锶90,它每年的衰减率为
,专家估计,要完全消除这次核事件对自然环境的影响至少需要800年,到那时原有的锶90还剩百分之几?
归纳总结
通过本节课的学习,你有哪些收获?
一个函数:指数函数
两个模型及特点:
研究指数函数的基本思路:
实际应用
实际背景
数量关系
函数概念
指数增长
指数衰减
单元知识框架
概念
指数函数
概念
指数函数
图象、性质
当堂检测
1.若指数增长型函数为 N ,则每次的增长率为_____.
2.若指数衰减型函数为 N ,则每次的衰减率为______.
4.在问题2中,如果把死亡的生物体内碳14含量看成1个单位,则它体内碳14的含量衰减为原来的 需要经过多少年?
3.下列图象中,有可能表示指数函数的是( )
C
不努力原地踏步,
多努力爆炸式进步
作业布置
必做:课本115页练习1,2,3;课本119页习题4,2第4题,第7题
探究作业:数学建模活动:选择生活中的实例构建指数增长模型
选做:列表,描点,在同一直角坐标系中作出
的图象
THANKS
延时符
4.2.1 指数函数的概念
单元知识框架
实际情境
数量关系
抽象
函数形式
归纳
图象、性质
研究
实际应用
解决
概念
指数函数
实数指数幂
学习目标
二.学习重点与难点
重点:指数函数的概念
难点:概括指数函数概念的过程,对指数函数的理解
一.学习目标
(1)通过具体实例,了解指数函数的实际意义,理解指数函数的概念.
(2)体会指数函数概念的形成过程,提升数学抽象、逻辑推理和数学建 模核心素养.
新知探究
问题1 随着中国经济高速增长,人民生活水平不断提高,旅游成了越来越多家庭的重要生活方式.由于旅游人数不断增加,A,B两地景区自2001年起采取了不同的应对措施:
A地提高了景区门票价格,
而B地则取消了景区门票.
下表给出了A,B两地景区2001年至2015年的游客人次以及逐年增加量.
比较两地景区游客人次的变化情况.你发现了怎样的变化规律?
时间/年A地景区B地景区人次/万次年增加量/万次人次/万次年增加量/万次2001600 278 2002609309200362034420046313832005641427200665047520076615282008671588200968165520106917292011702811201271190320137211005201473211182015743124491111109111010101191011113135394448536067748292102113126追问1:观察A,B两地景区旅游人次变化情况,你发现了怎样的变化规律?追问2:B景区规律没有找到,能不能换个数学方法找规律?表格中,A景区人次的增加量基本相同,为10(左右);B景区人次的增加量不稳定,但越来越大.A地景区 时间/年 人次/万次
2001 600
2002 609
2003 620
2004 631
2005 641
2006 650
2007 661
2008 671
2009 681
2010 691
2011 702
2012 711
2013 721
2014 732
2015 743
B地景区 时间/年 人次/万次
2001 278
2002 309
2003 344
2004 383
2005 427
2006 475
2007 528
2008 588
2009 655
2010 729
2011 811
2012 903
2013 1005
2014 1118
2015 1244
近似直线上升,线性增长
非线性上升,越来越陡,
与A变化规律不同
B地景区 时间/年 人次/万次
2001 278
2002 309
2003 344
2004 383
2005 427
2006 475
2007 528
2008 588
2009 655
2010 729
2011 811
2012 903
2013 1005
2014 1118
2015 1244
…………
追问3:代数运算是寻找变化规律的基本方法.A地变化规律通过哪个不变量找到的?B地景区游客人次是否也可以用如类似这样的不变量来刻画呢?
试计算游客人次的年增长率
像这样,增长率为常数的变化方式,我们称为指数增长.
B地景区的游客人次的年增长率都约为
是一个常数.
1年后,游客人次是2001年的___________倍;
2年后,游客人次是2001年的___________倍;
3年后,游客人次是2001年的___________倍;
……
年后,游客人次是2001年的___________倍.
从2001年开始,B地景区游客人次的变化规律可以近似描述为:
如果设经过 年后的游客人次为2001年的 倍,
那么 =______________________
这是一个函数,其中指数 是自变量.
自变量增加1个单位,
小结:函数变化规律为:
新知探究(小组活动)
问题2 当生物死亡后,它机体内原有的碳14含量会按确定的比率衰减(称为衰减率),大约每经过5730年衰减为原来的一半,这个时间称为“半衰期“.
5730年
1
设死亡生物体内碳14含量的年衰减率为p,把刚死亡的生物体内碳14的含量看成1个单位
按照上述变化规律,类比问题1的探究过程,完成下面3个问题:
像这样,衰减率为常数的变化方式,我们称为指数衰减.
追问1:按规律,填写表格
死亡年数x
1年
2年
3年
······
5730年
年
碳14含量y
追问2:生物体内碳14含量y与死亡年数x之间有怎样的关系?
追问3:求出生物死亡后体内碳14含量年衰减率 的值.
小结:函数变化规律为:
自变量增加1个单位,
则:y与x的函数关系为:
概念抽象
问题:以上函数的解析式有何共同特征?能否用一个式子来反映这些特征?
一般地,函数 叫做指数函数,其中指数x是自变量,定义域是R.
指数
指数
指数
常数
常数
常数
幂
幂
幂
自变量的位置
底数
形式
函数解析式
新知应用
例1 已知函数
(1)求函数 的解析式;
(2)求 的值.
新知应用
例2 (1)在问题1中,平均每位游客出游一次可给当地带来1000元门票之外的收入,A地景区的门票价格为150元,比较这15年间A,B两地旅游收入变化情况.
前情提要:A地景区2001年旅游人次600万,年增加量10万人次;
B地景区2001年旅游人次278万,年增长率0.11.
(1)建立经过x年,游客给A,B两地带来的旅游收入的函数f(x)和g(x).
(2)如何比较 f(x)和g(x)大小?
(3)通过图象之间的关系,描述15年间A,B两地景区的收入变化情况.
思路分析:
新知应用
把形如 的函数称为指数型函数.
指数增长模型:设原有量为 ,每次的增长率为 则经过 次增长,该量增长到 则
指数衰减模型:设原有量为 ,每次的衰减率为 则经过 次衰减,该量减少到 则
指数增长
指数衰减
( N, )
( N, )
课堂练习
解:设核电站爆炸时锶90最初的量为
依题意,经过 年后,锶90的量变为
所以,800年后原有的锶90还剩
1986年4月26日,乌克兰境内的切尔诺贝利核电站爆炸,核泄漏导致事故所在地被严重污染.主要的核污染物是锶90,它每年的衰减率为
,专家估计,要完全消除这次核事件对自然环境的影响至少需要800年,到那时原有的锶90还剩百分之几?
归纳总结
通过本节课的学习,你有哪些收获?
一个函数:指数函数
两个模型及特点:
研究指数函数的基本思路:
实际应用
实际背景
数量关系
函数概念
指数增长
指数衰减
单元知识框架
概念
指数函数
概念
指数函数
图象、性质
当堂检测
1.若指数增长型函数为 N ,则每次的增长率为_____.
2.若指数衰减型函数为 N ,则每次的衰减率为______.
4.在问题2中,如果把死亡的生物体内碳14含量看成1个单位,则它体内碳14的含量衰减为原来的 需要经过多少年?
3.下列图象中,有可能表示指数函数的是( )
C
不努力原地踏步,
多努力爆炸式进步
作业布置
必做:课本115页练习1,2,3;课本119页习题4,2第4题,第7题
探究作业:数学建模活动:选择生活中的实例构建指数增长模型
选做:列表,描点,在同一直角坐标系中作出
的图象
THANKS
延时符
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
