28.1锐角三角函数第2课时(余弦与余切)课件 2022—2023学年人教版数学九年级下册(22张PPT)
文档属性
| 名称 | 28.1锐角三角函数第2课时(余弦与余切)课件 2022—2023学年人教版数学九年级下册(22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 23.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 00:00:00 | ||
图片预览





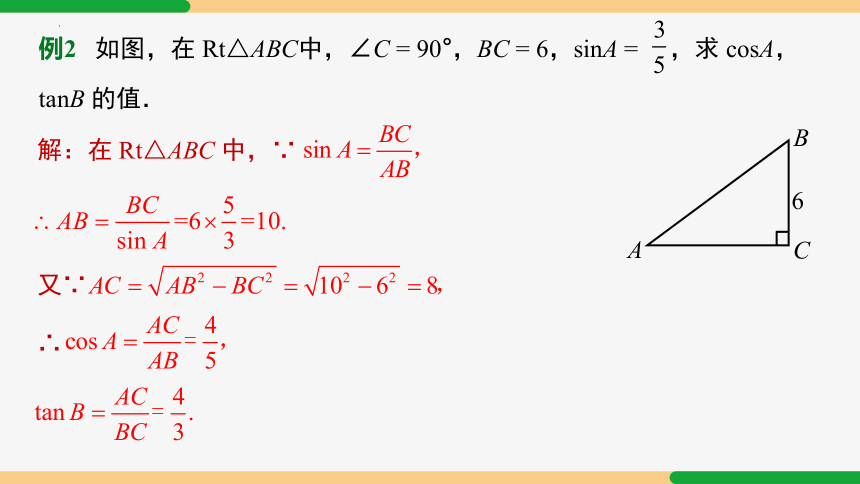
文档简介
(共22张PPT)
余弦与余切
| 28.1 锐角三角函数
| 28.1 锐角三角函数 第2课时 |
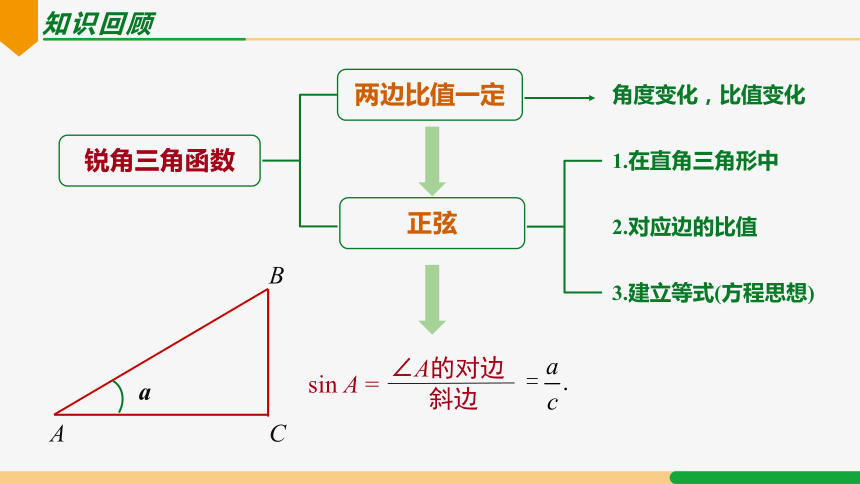
知识回顾
还有那些锐角三角函数?
知识回顾
A
B
C
a
锐角三角函数
两边比值一定
正弦
∠A的对边
斜边
sin A =
1.在直角三角形中
2.对应边的比值
3.建立等式(方程思想)
角度变化,比值变化
新知探究
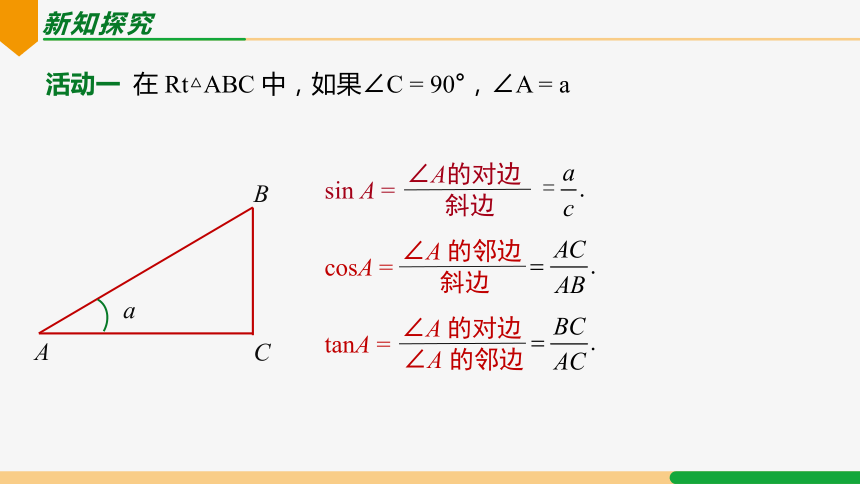
活动一 在 Rt△ABC 中,如果∠C = 90°,∠A = a
A
B
C
a
∠A的对边
斜边
sin A =
∠A 的邻边
斜边
cosA =
∠A 的对边
∠A 的邻边
tanA =
当在 Rt△ABC 中,∠C=90°,
锐角 A 的对边与斜边的比叫做∠A 的正弦,记作 sinA
锐角 A 的邻边与斜边的比叫做∠A 的余弦,记作 cosA,
锐角 A 的对边与邻边的比叫做∠A 的正切,记作 tanA
锐角三角函数
A
B
C
a
∠A的对边
斜边
sin A =
∠A 的邻边
斜边
cosA =
∠A 的对边
∠A 的邻边
tanA =
典例讲解
例1 如图,在 Rt△ABC 中,∠C = 90°,AB = 10,BC = 6,求 sinA,cosA,tanA 的值.
A
B
C
解:由勾股定理得
∴
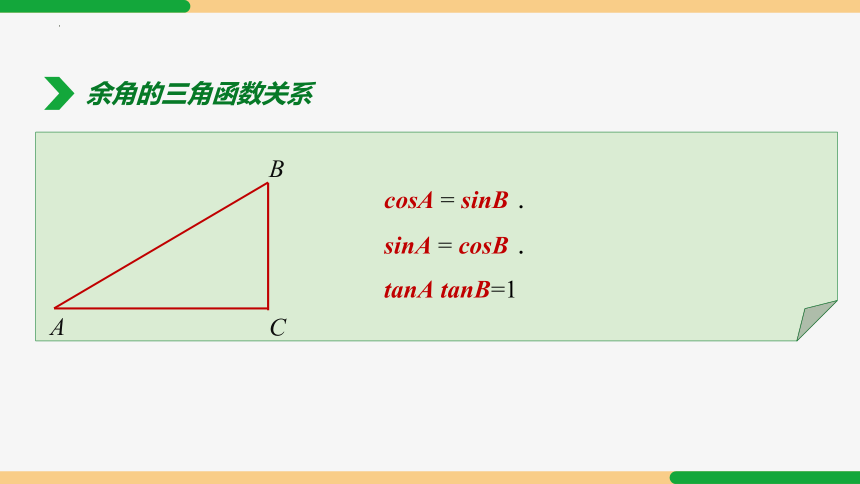
cosA = sinB.
sinA = cosB.
tanA tanB=1
余角的三角函数关系
A
B
C
针对练习
1. 在Rt△ABC中,∠C = 90°,AC = 12,AB =13.
sinA =______,cosA =______,tanA =____,
sinB =______,cosB =______,tanB =____.
A
B
C
12
13
A
B
C
6
例2 如图,在 Rt△ABC中,∠C = 90°,BC = 6,sinA = ,求 cosA,tanB 的值.
解:在 Rt△ABC 中,∵
又∵
∴
例3 如图,在△ABC中,AB = AC = 4,BC = 6. 求 cosB 及 tanB 的值.
解:过点 A 作 AD⊥BC 于点 D.
∵ AB = AC,BC = 6,
∴ BD = CD = 3.
在 Rt△ABD 中,
∴ tanB =
A
B
C
∴
D
例4 如图,已知四边形ABCD 内接于⊙O,A是 的中点, AE⊥AC 于A,与⊙O 及CB 的延长线交于点F,E,且 .
(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD 的值.
知识回顾
A
B
C
a
锐角三角函数
两边比值一定
正弦
∠A的对边
斜边
sin A =
余弦
正切
∠A 的邻边
斜边
cosA =
∠A 的对边
∠A 的邻边
tanA =
cosA = sinB.
sinA = cosB.
tanA tanB=1
互余三角函数
课堂练习
在 Rt△ABC 中,∠C = 90°,AC = 2,BC = 3.
sinA =_______,cosA =_______,tanA =_____,
sinB =_______,cosB =_______,tanB =_____.
B
C
2
3
A
如图,在平面直角坐标系中,若点 P 坐标为 (3,4),连接 OP,则 OP 与 x 轴正方向所夹锐角 α 的正切值为_____.
α
如图,△ABC 中一边 BC 与以 AC 为直径的 ⊙O相切与点 C,若 BC = 4,AB = 5,则 tanA =___.
·
A
O
B
C
如图,在 Rt△ABC 中,斜边 AB 的长为 m, ∠A = 35°,则直角边 BC 的长是 ( )
A.
B.
C.
D.
A
A
B
C
sin70°,cos70°,tan70° 的大小关系是 ( )
A. tan70°<cos70°<sin70°
B. cos70°<tan70°<sin70°
C. sin70°<cos70°<tan70°
D. cos70°<sin70°<tan70°
D
如图,在 Rt△ABC 中,∠C = 90°,cosA =,求 sinA,tanA 的值.
解:在 Rt△ABC 中,由
A
B
C
设 AC = 15k,则 AB = 17k.
∴
∴
如图,在 Rt△ABC 中,∠ACB = 90°,CD⊥AB,垂足为 D. 若 AD = 6,CD = 8. 求 tanB 的值.
解: ∵ CD⊥AB,∠ACB =∠ADC = 90°,
∴∠B +∠A = 90°,
∠ACD +∠A = 90°.
∴∠B = ∠ACD.
∴ tan∠B = tan∠ACD =
如图,在等腰三角形ABC 中,AC=BC=10,AB=12,以BC 为直径作⊙O 交AB 于点D,交AC 于点G,DF⊥AC,垂足为F,交CB 的延长线于点E.
(1)求证:直线EF 是⊙O 的切线;
(2)求cos E 的值.
(1)证明:如图,连接OD,CD.
∵BC 是直径,
∴CD⊥AB.
∵AC=BC,
∴D 是AB的中点.
又∵O 为CB 的中点,
∴OD∥AC.
∵DF⊥AC,
∴OD⊥EF,
∴EF 是⊙O 的切线.
(2)解:如图,连接BG. ∵BC 是直径,
∴∠BGC=90°.
在Rt△ACD 中,DC= ==8.
∵AB ·CD=2S△ABC=AC ·BG,
∴BG===
∵BG⊥AC,DF⊥AC,
∴BG∥EF,
∴∠E=∠CBG.
∴cos E=cos ∠CBG= =
余弦与余切
| 28.1 锐角三角函数
| 28.1 锐角三角函数 第2课时 |
知识回顾
还有那些锐角三角函数?
知识回顾
A
B
C
a
锐角三角函数
两边比值一定
正弦
∠A的对边
斜边
sin A =
1.在直角三角形中
2.对应边的比值
3.建立等式(方程思想)
角度变化,比值变化
新知探究
活动一 在 Rt△ABC 中,如果∠C = 90°,∠A = a
A
B
C
a
∠A的对边
斜边
sin A =
∠A 的邻边
斜边
cosA =
∠A 的对边
∠A 的邻边
tanA =
当在 Rt△ABC 中,∠C=90°,
锐角 A 的对边与斜边的比叫做∠A 的正弦,记作 sinA
锐角 A 的邻边与斜边的比叫做∠A 的余弦,记作 cosA,
锐角 A 的对边与邻边的比叫做∠A 的正切,记作 tanA
锐角三角函数
A
B
C
a
∠A的对边
斜边
sin A =
∠A 的邻边
斜边
cosA =
∠A 的对边
∠A 的邻边
tanA =
典例讲解
例1 如图,在 Rt△ABC 中,∠C = 90°,AB = 10,BC = 6,求 sinA,cosA,tanA 的值.
A
B
C
解:由勾股定理得
∴
cosA = sinB.
sinA = cosB.
tanA tanB=1
余角的三角函数关系
A
B
C
针对练习
1. 在Rt△ABC中,∠C = 90°,AC = 12,AB =13.
sinA =______,cosA =______,tanA =____,
sinB =______,cosB =______,tanB =____.
A
B
C
12
13
A
B
C
6
例2 如图,在 Rt△ABC中,∠C = 90°,BC = 6,sinA = ,求 cosA,tanB 的值.
解:在 Rt△ABC 中,∵
又∵
∴
例3 如图,在△ABC中,AB = AC = 4,BC = 6. 求 cosB 及 tanB 的值.
解:过点 A 作 AD⊥BC 于点 D.
∵ AB = AC,BC = 6,
∴ BD = CD = 3.
在 Rt△ABD 中,
∴ tanB =
A
B
C
∴
D
例4 如图,已知四边形ABCD 内接于⊙O,A是 的中点, AE⊥AC 于A,与⊙O 及CB 的延长线交于点F,E,且 .
(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD 的值.
知识回顾
A
B
C
a
锐角三角函数
两边比值一定
正弦
∠A的对边
斜边
sin A =
余弦
正切
∠A 的邻边
斜边
cosA =
∠A 的对边
∠A 的邻边
tanA =
cosA = sinB.
sinA = cosB.
tanA tanB=1
互余三角函数
课堂练习
在 Rt△ABC 中,∠C = 90°,AC = 2,BC = 3.
sinA =_______,cosA =_______,tanA =_____,
sinB =_______,cosB =_______,tanB =_____.
B
C
2
3
A
如图,在平面直角坐标系中,若点 P 坐标为 (3,4),连接 OP,则 OP 与 x 轴正方向所夹锐角 α 的正切值为_____.
α
如图,△ABC 中一边 BC 与以 AC 为直径的 ⊙O相切与点 C,若 BC = 4,AB = 5,则 tanA =___.
·
A
O
B
C
如图,在 Rt△ABC 中,斜边 AB 的长为 m, ∠A = 35°,则直角边 BC 的长是 ( )
A.
B.
C.
D.
A
A
B
C
sin70°,cos70°,tan70° 的大小关系是 ( )
A. tan70°<cos70°<sin70°
B. cos70°<tan70°<sin70°
C. sin70°<cos70°<tan70°
D. cos70°<sin70°<tan70°
D
如图,在 Rt△ABC 中,∠C = 90°,cosA =,求 sinA,tanA 的值.
解:在 Rt△ABC 中,由
A
B
C
设 AC = 15k,则 AB = 17k.
∴
∴
如图,在 Rt△ABC 中,∠ACB = 90°,CD⊥AB,垂足为 D. 若 AD = 6,CD = 8. 求 tanB 的值.
解: ∵ CD⊥AB,∠ACB =∠ADC = 90°,
∴∠B +∠A = 90°,
∠ACD +∠A = 90°.
∴∠B = ∠ACD.
∴ tan∠B = tan∠ACD =
如图,在等腰三角形ABC 中,AC=BC=10,AB=12,以BC 为直径作⊙O 交AB 于点D,交AC 于点G,DF⊥AC,垂足为F,交CB 的延长线于点E.
(1)求证:直线EF 是⊙O 的切线;
(2)求cos E 的值.
(1)证明:如图,连接OD,CD.
∵BC 是直径,
∴CD⊥AB.
∵AC=BC,
∴D 是AB的中点.
又∵O 为CB 的中点,
∴OD∥AC.
∵DF⊥AC,
∴OD⊥EF,
∴EF 是⊙O 的切线.
(2)解:如图,连接BG. ∵BC 是直径,
∴∠BGC=90°.
在Rt△ACD 中,DC= ==8.
∵AB ·CD=2S△ABC=AC ·BG,
∴BG===
∵BG⊥AC,DF⊥AC,
∴BG∥EF,
∴∠E=∠CBG.
∴cos E=cos ∠CBG= =
