28.2.2应用举例第2课时 (仰俯角) 课件2022—2023学年人教版数学九年级下册(19张PPT)
文档属性
| 名称 | 28.2.2应用举例第2课时 (仰俯角) 课件2022—2023学年人教版数学九年级下册(19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 24.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 19:51:47 | ||
图片预览





文档简介
(共19张PPT)
仰角、俯角问题
| 28.2 解直角三角形及其应用
| 28.2.2 应用举例 第2课时 |
知识导航
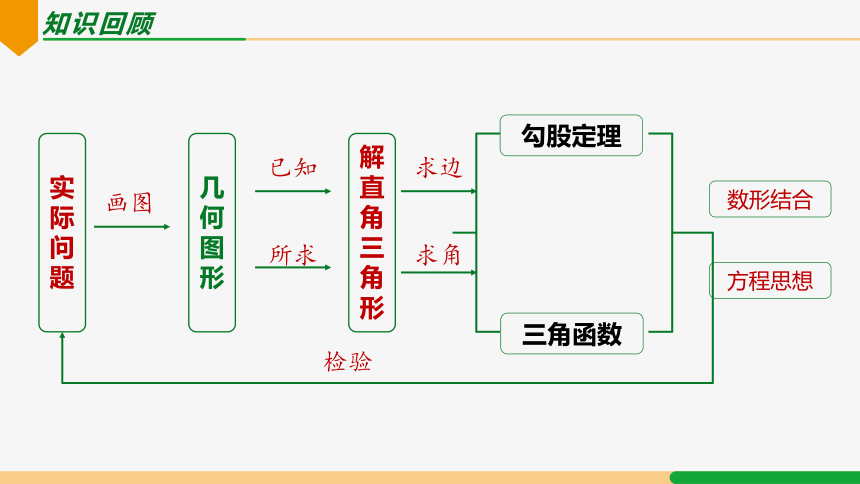
解直角三角形能解决那些实际问题?
知识回顾
实际问题
勾股定理
三角函数
画图
几何图形
解直角三角形
已知
所求
求边
求角
数形结合
方程思想
检验
典例讲解
例1 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为 30°,看这栋高楼底部的俯角为 60°,热气球与高楼的水平距离为 120 m,这栋高楼有多高(结果精确到 0.1 m)?
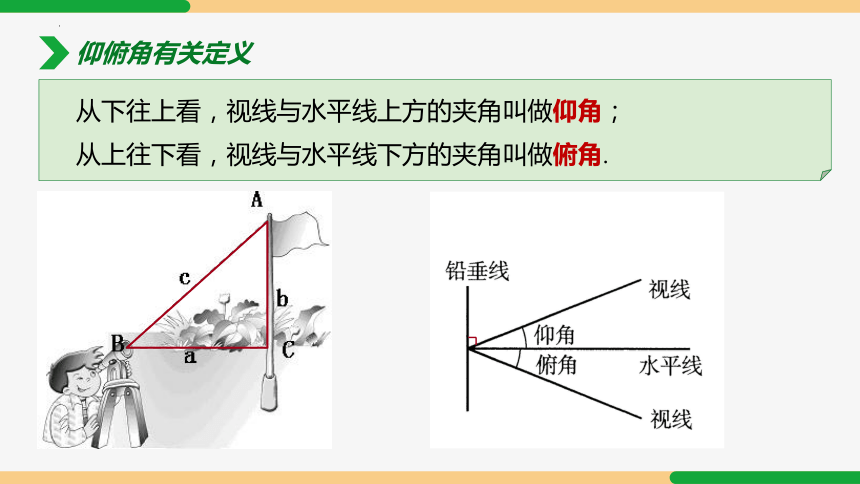
仰俯角有关定义
从下往上看,视线与水平线上方的夹角叫做仰角;
从上往下看,视线与水平线下方的夹角叫做俯角.
解:如图,α = 30°,β = 60°, AD = 120.
答:这栋楼高约为 277.1 m.
D
α
β
例2 如图,小明想测量塔 AB 的高度.他在 D 处仰望塔顶,测得仰角为 30°,再往塔的方向前进 50 m 至 C 处.测得仰角为 60°,小明的身高 1.5 m.那么该塔有多高 (结果精确到 1 m),你能帮小明算出该塔有多高吗
D′
A
B′
B
D
C′
C
解:如图,设 AB′ = x m.
由题意知∠AD′B′ = 30°,∠AC′B′ = 60°, D′C′ = 50 m.
∴∠D′AB′ = 60°,∠C′AB′ = 30°,D′C′ = 50 m ,
D′
A
B′
B
D
C′
C
例3 如图,直升飞机在长 400 米的跨江大桥 AB 的上方 P 点处,在大桥的两端测得飞机的仰角分别为 37° 和 45°,求飞机的高度.(结果取整数. 参考数据:sin37°≈ 0.6,cos37° ≈ 0.8,tan 37° ≈ 0.75)
A
B
37°
45°
P
A
B
O
37°
45°
400 米
P
在 Rt△POB 中,∠PBO = 45°,
在 Rt△POA 中,∠PAB = 37°,
∴ OB = PO = x 米.
解得 x = 1200.
解:作 PO⊥AB 交 AB 的延长线于点 O,设 PO = x 米.
即
故飞机的高度为 1200 米.
知识小结
A
D
B
E
C
α
β
α
β
α
β
α
β
仰俯角相关模型
课堂练习
如图,为测量一棵与地面垂直的树OA 的高度,在距离树的底端30米的B 处,测得树顶A 的仰角∠ABO 为α,则树OA的高度为( )
A.
B.30sin α米
C.30tan α米
D.30cos α米
C
湖南路大桥于今年5月1日竣工,为徒骇河景区增添了一道亮丽的风景线.某校数学兴趣小组用测量仪器测量该大桥的桥塔高度,在距桥塔AB 底部50米的C 处,测得桥塔顶部A 的仰角为41.5°(如图).已知测量仪器CD 的高度为1米,则桥塔AB 的高度约为( )(参考数据:sin 41.5°≈0.663,cos 41.5°≈0.749,tan 41.5°≈0.885)
A.34米 B.38米
C.45米 D.50米
C
如图,两建筑物 AB 和 CD 的水平距离为 30 米,从A点测得 D 点的俯角为30°,测得 C 点的俯角为 60°,则建筑物 CD 的高为_____米.
B
C
A
D
30°
60°
如图,在电线杆上离地面高度 5 m 的 C 点处引两根拉线固定电线杆,一根拉线 AC 和地面成 60° 角,另一根拉线 BC 和地面成 45° 角.则两根拉线的总长度为 m (结果 保留根号).
如图,某人为了测量小山顶上的塔ED 的高,他在山下的点A 处测得塔尖点D 的仰角为45°,再沿AC 方向前进60 m 到达山脚点B,测得塔尖点D 的仰角为60°,塔底点E 的仰角为30°,求塔ED 的高度.(结果保留根号)
由题知,∠DBC=60°,∠EBC=30°,
∴∠DBE=∠DBC-∠EBC=60°-30°=30°.又∵∠BCD=90°,
∴∠BDC=90°-∠DBC=90°-60°=30°.
∴∠DBE=∠BDE.∴BE=DE.
设EC=x,则DE=BE=2EC=2x,DC=EC+DE=x+2x=3x,∴BC===
由题知,∠DAC=45°,∠DCA=90°,AB=60,
∴△ACD 为等腰直角三角形.∴AC=DC.
∴x+60=x,解得x=30+10.
∴DE=2x=60+20 .
答:塔ED 的高为(60+20 )m.
解:
金桥学校“科技体艺节”期间,八年级数学活动小组的任务是测量学校旗杆AB 的高,他们在旗杆正前方台阶上的点C 处,测得旗杆顶端A 的仰角为45°,朝着旗杆的方向走到台阶下的点F 处,测得旗杆顶端A的仰角为60°,已知升旗台的高度BE 为1米,点C 距地面的高度CD 为3米,台阶CF 的坡角为30°,且点E,F,D 在同一条直线上,求旗杆AB 的高度.(计算结果精确到0.1米,参考数据: ≈1.41, ≈1.73)
解:
如图所示,过点C 作CM⊥AB 于点M,则四边形MEDC 是矩形,
∴ME=DC=3,CM=ED.
在Rt△AEF 中,∠AFE=60°,
设EF=x,则AF=2x,AE=x.
在Rt△FCD 中,CD=3,∠CFD=30°, ∴DF=3.
在Rt△AMC 中,∠ACM=45°,
∴MA=MC. ∵ED=MC, ∴AM=ED.
∵AM=AE-ME,ED=EF+DF,
∴x-3=x+3 . 解得x=6+3 .
∴AE=×(6+3 )=6+9.
∴AB=AE-BE=9+6-1≈18.4(米).
答:旗杆AB 的高度约为18.4米.
仰角、俯角问题
| 28.2 解直角三角形及其应用
| 28.2.2 应用举例 第2课时 |
知识导航
解直角三角形能解决那些实际问题?
知识回顾
实际问题
勾股定理
三角函数
画图
几何图形
解直角三角形
已知
所求
求边
求角
数形结合
方程思想
检验
典例讲解
例1 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为 30°,看这栋高楼底部的俯角为 60°,热气球与高楼的水平距离为 120 m,这栋高楼有多高(结果精确到 0.1 m)?
仰俯角有关定义
从下往上看,视线与水平线上方的夹角叫做仰角;
从上往下看,视线与水平线下方的夹角叫做俯角.
解:如图,α = 30°,β = 60°, AD = 120.
答:这栋楼高约为 277.1 m.
D
α
β
例2 如图,小明想测量塔 AB 的高度.他在 D 处仰望塔顶,测得仰角为 30°,再往塔的方向前进 50 m 至 C 处.测得仰角为 60°,小明的身高 1.5 m.那么该塔有多高 (结果精确到 1 m),你能帮小明算出该塔有多高吗
D′
A
B′
B
D
C′
C
解:如图,设 AB′ = x m.
由题意知∠AD′B′ = 30°,∠AC′B′ = 60°, D′C′ = 50 m.
∴∠D′AB′ = 60°,∠C′AB′ = 30°,D′C′ = 50 m ,
D′
A
B′
B
D
C′
C
例3 如图,直升飞机在长 400 米的跨江大桥 AB 的上方 P 点处,在大桥的两端测得飞机的仰角分别为 37° 和 45°,求飞机的高度.(结果取整数. 参考数据:sin37°≈ 0.6,cos37° ≈ 0.8,tan 37° ≈ 0.75)
A
B
37°
45°
P
A
B
O
37°
45°
400 米
P
在 Rt△POB 中,∠PBO = 45°,
在 Rt△POA 中,∠PAB = 37°,
∴ OB = PO = x 米.
解得 x = 1200.
解:作 PO⊥AB 交 AB 的延长线于点 O,设 PO = x 米.
即
故飞机的高度为 1200 米.
知识小结
A
D
B
E
C
α
β
α
β
α
β
α
β
仰俯角相关模型
课堂练习
如图,为测量一棵与地面垂直的树OA 的高度,在距离树的底端30米的B 处,测得树顶A 的仰角∠ABO 为α,则树OA的高度为( )
A.
B.30sin α米
C.30tan α米
D.30cos α米
C
湖南路大桥于今年5月1日竣工,为徒骇河景区增添了一道亮丽的风景线.某校数学兴趣小组用测量仪器测量该大桥的桥塔高度,在距桥塔AB 底部50米的C 处,测得桥塔顶部A 的仰角为41.5°(如图).已知测量仪器CD 的高度为1米,则桥塔AB 的高度约为( )(参考数据:sin 41.5°≈0.663,cos 41.5°≈0.749,tan 41.5°≈0.885)
A.34米 B.38米
C.45米 D.50米
C
如图,两建筑物 AB 和 CD 的水平距离为 30 米,从A点测得 D 点的俯角为30°,测得 C 点的俯角为 60°,则建筑物 CD 的高为_____米.
B
C
A
D
30°
60°
如图,在电线杆上离地面高度 5 m 的 C 点处引两根拉线固定电线杆,一根拉线 AC 和地面成 60° 角,另一根拉线 BC 和地面成 45° 角.则两根拉线的总长度为 m (结果 保留根号).
如图,某人为了测量小山顶上的塔ED 的高,他在山下的点A 处测得塔尖点D 的仰角为45°,再沿AC 方向前进60 m 到达山脚点B,测得塔尖点D 的仰角为60°,塔底点E 的仰角为30°,求塔ED 的高度.(结果保留根号)
由题知,∠DBC=60°,∠EBC=30°,
∴∠DBE=∠DBC-∠EBC=60°-30°=30°.又∵∠BCD=90°,
∴∠BDC=90°-∠DBC=90°-60°=30°.
∴∠DBE=∠BDE.∴BE=DE.
设EC=x,则DE=BE=2EC=2x,DC=EC+DE=x+2x=3x,∴BC===
由题知,∠DAC=45°,∠DCA=90°,AB=60,
∴△ACD 为等腰直角三角形.∴AC=DC.
∴x+60=x,解得x=30+10.
∴DE=2x=60+20 .
答:塔ED 的高为(60+20 )m.
解:
金桥学校“科技体艺节”期间,八年级数学活动小组的任务是测量学校旗杆AB 的高,他们在旗杆正前方台阶上的点C 处,测得旗杆顶端A 的仰角为45°,朝着旗杆的方向走到台阶下的点F 处,测得旗杆顶端A的仰角为60°,已知升旗台的高度BE 为1米,点C 距地面的高度CD 为3米,台阶CF 的坡角为30°,且点E,F,D 在同一条直线上,求旗杆AB 的高度.(计算结果精确到0.1米,参考数据: ≈1.41, ≈1.73)
解:
如图所示,过点C 作CM⊥AB 于点M,则四边形MEDC 是矩形,
∴ME=DC=3,CM=ED.
在Rt△AEF 中,∠AFE=60°,
设EF=x,则AF=2x,AE=x.
在Rt△FCD 中,CD=3,∠CFD=30°, ∴DF=3.
在Rt△AMC 中,∠ACM=45°,
∴MA=MC. ∵ED=MC, ∴AM=ED.
∵AM=AE-ME,ED=EF+DF,
∴x-3=x+3 . 解得x=6+3 .
∴AE=×(6+3 )=6+9.
∴AB=AE-BE=9+6-1≈18.4(米).
答:旗杆AB 的高度约为18.4米.
