2022—2023学年人教版数学九年级下册28.2.1解直角三角形 课件(共23张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学九年级下册28.2.1解直角三角形 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 23.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 20:23:18 | ||
图片预览



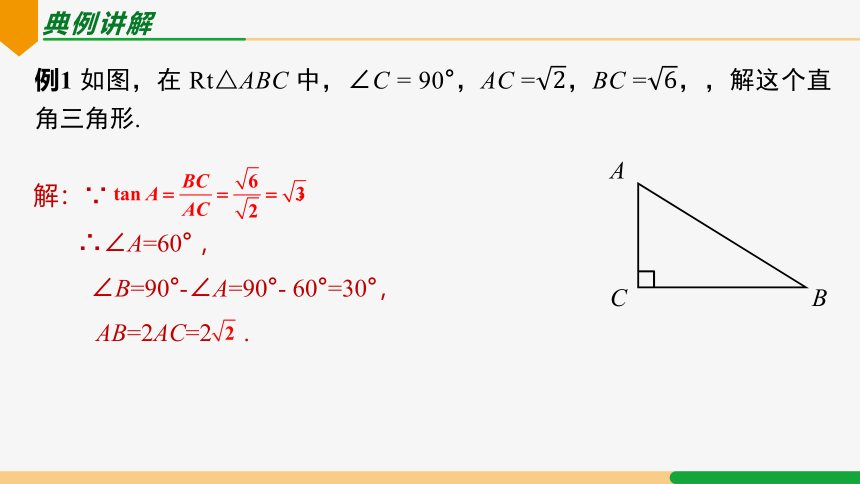



文档简介
(共23张PPT)
解直角三角形
| 28.2 解直角三角形及其应用
| 28.2.1 解直角三角形 第1课时 |
知识导航
学习锐角的三角函数有什么作用?
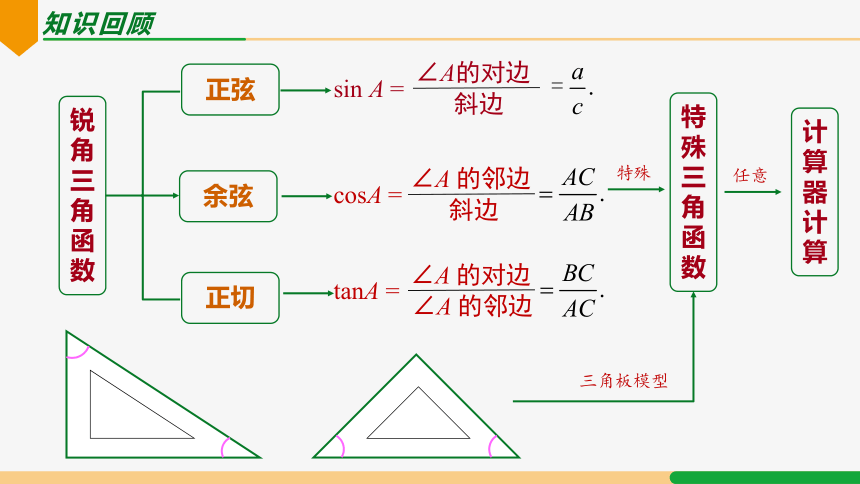
知识回顾
锐角三角函数
正弦
∠A的对边
斜边
sin A =
余弦
正切
∠A 的邻边
斜边
cosA =
∠A 的对边
∠A 的邻边
tanA =
特殊
特殊三角函数
三角板模型
计算器计算
任意
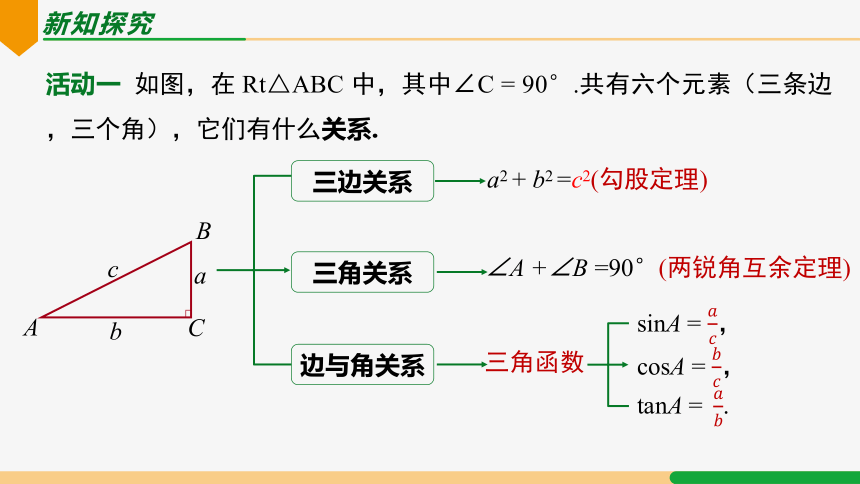
新知探究
活动一 如图,在 Rt△ABC 中,其中∠C = 90°.共有六个元素(三条边,三个角),它们有什么关系.
C
c
b
a
A
B
三边关系
三角关系
边与角关系
a2 + b2 =c2(勾股定理)
∠A +∠B =90°(两锐角互余定理)
三角函数
sinA = ,
cosA = ,
tanA =.
由直角三角形中的已知元素(至少有一个是边),求出其余未知元素的过程,叫做解直角三角形
解直角三角形
C
c
b
a
A
B
典例讲解
例1 如图,在 Rt△ABC 中,∠C = 90°,AC =,BC =,,解这个直角三角形.
A
B
C
解:∵
∴∠A=60° ,
∠B=90°-∠A=90°- 60°=30°,
AB=2AC=2 .
例2 如图,在 Rt△ABC 中,∠C = 90°,∠B = 35°,b = 20,解这个直角三角形 (结果保留小数点后一位).
A
B
C
b
c
a
35°
解:
针对练习
在Rt△ABC 中,∠C=90°,AB=2,AC= ,则∠A 的度数为( )
A.90° B.60° C.45° D.30°
D
在△ABC 中,∠C=90°,AB=4,AC=3,欲求∠A的值,最适宜的做法是( )
A.计算tan A 的值求出 B.计算sin A 的值求出
C.计算cos A 的值求出
D.先根据sin B 求出∠B,再利用90°-∠B 求出
C
例3 如图,在 Rt△ABC 中,∠C = 90°,cosA = ,BC = 5, 试求 AB 的长.
A
C
B
解:
设
例4 如图,在△ABC 中,AB=1,AC=,sin B =,求BC 的长.
A
C
B
如图,过点A 作AD⊥BC 于点D.
∵AB=1,sin B=
∴AD=AB · sin B=
∴BD=
∴CD=
∴BC=CD+BD=
解:
知识小结
解直角三角形
定义
依据
思想
三边关系
三角关系
边与角关系
a2 + b2 =c2(勾股定理)
∠A +∠B =90°(两锐角互余定理)
三角函数
sinA = ,
cosA = ,
tanA =.
数形结合、方程思想
课堂练习
2. 如图,在 Rt△ABC 中,∠C = 90°,∠B = 30°, AB = 8,则 BC 的长是 ( )
D
1. 在 Rt△ABC 中,∠C = 90°,a,b,c 分别是∠A, ∠B,∠C 的对边,则下列各式正确的是 ( )
A. b = a·tanA B. b = c·sinA
C. b = c·cosA D. a = c·cosA
A
C
B
C
在 Rt△ABC 中,∠C = 90°,∠B = 37°,BC = 32, 则 AC = (参考数据:sin37° ≈ 0.60,cos37° ≈ 0.80,tan37° ≈ 0.75).
如图,已知 Rt△ABC 中,斜边 BC 上的高 AD = 3,cosB = ,则 AC 的长为 .
24
3.75
如图,在 Rt△ABC 中,∠C = 90°,AC = 6,角平分线 ,解这个直角三角形.
解:
∵ AD 平分∠BAC,
D
A
B
C
6
如图,已知 AC = 4,求 AB 和 BC 的长.
在 Rt△CDB 中,∠DCB =∠ACB-∠ACD = 45°,
解:如图,作 CD⊥AB 于点 D.
在 Rt△ACD 中,∵∠A = 30°,∴∠ACD = 90° - ∠A = 60°.
∴ BD = CD = 2.
D
解:过点 A 作 AD⊥BC 于点 D.
在△ACD 中,∠C = 45°,AC = 2,
∴ CD = AD = sinC · AC = 2sin45° = .
在△ABD 中,∠B = 30°,
∴ BD =
∴ BC = CD + BD =
如图,在△ABC 中,∠B = 30°,∠C = 45°,AC = 2,求 BC 的长.
D
A
B
C
在△ABC 中,AB = ,AC = 13,cosB = ,求 BC 的长.
图②
图①
解:∵cosB = ,∴∠B = 45°.
当△ABC 为钝角三角形时,如图①.
∵AC = 13,∴由勾股定理得 CD = 5.
∴BC = BD + CD = 12 + 5 = 17
当△ABC 为锐角三角形时,如图②,
此时 .BC = BD - CD = 12 - 5 = 7.
综上可知,BC 的长为 7 或 17.
图②
图①
如图,PB 为⊙O 的切线,B 为切点,过B 作OP 的垂线BA,垂足为C,交⊙O于点A,连接PA,AO.并延长AO 交⊙O 于点E,与PB 的延长线交于点D.
(1)求证:PA 是⊙O 的切线;
(2)若 ,且OC=4,求PA 的长和tan D 的值.
(1)证明:如图,连接BO,
∵PB 为⊙O 的切线,B 为切点,
∴OB⊥PD,∠PBO=90°.
又∵OA=OB,OC⊥AB,
∴∠AOC=∠BOC.
又∵OP=OP,
∴△PAO ≌ △PBO,
∴∠PAO=∠PBO=90°,
∴PA 是⊙O 的切线.
(2)解:∵∠ACO=∠PAO=90°,∠AOC=∠POA,
∴△AOC∽△POA,∴ .
又∵OC=4,∴AC=6.
在Rt△AOC 中,
OA= ,
∴PA=OA=3,又易知PA=PB,∴PB=3.
在Rt△PAO 中,
PO= =13.
如图,连接BE. ∵AE 为直径,∴∠ABE=90°.
又∵OC⊥AB,∴BE∥OP,
∴△DBE∽△DPO,BE=2OC=8.
∴ .
即 .解得BD .
∴在Rt△DBO 中,tan D= .
解直角三角形
| 28.2 解直角三角形及其应用
| 28.2.1 解直角三角形 第1课时 |
知识导航
学习锐角的三角函数有什么作用?
知识回顾
锐角三角函数
正弦
∠A的对边
斜边
sin A =
余弦
正切
∠A 的邻边
斜边
cosA =
∠A 的对边
∠A 的邻边
tanA =
特殊
特殊三角函数
三角板模型
计算器计算
任意
新知探究
活动一 如图,在 Rt△ABC 中,其中∠C = 90°.共有六个元素(三条边,三个角),它们有什么关系.
C
c
b
a
A
B
三边关系
三角关系
边与角关系
a2 + b2 =c2(勾股定理)
∠A +∠B =90°(两锐角互余定理)
三角函数
sinA = ,
cosA = ,
tanA =.
由直角三角形中的已知元素(至少有一个是边),求出其余未知元素的过程,叫做解直角三角形
解直角三角形
C
c
b
a
A
B
典例讲解
例1 如图,在 Rt△ABC 中,∠C = 90°,AC =,BC =,,解这个直角三角形.
A
B
C
解:∵
∴∠A=60° ,
∠B=90°-∠A=90°- 60°=30°,
AB=2AC=2 .
例2 如图,在 Rt△ABC 中,∠C = 90°,∠B = 35°,b = 20,解这个直角三角形 (结果保留小数点后一位).
A
B
C
b
c
a
35°
解:
针对练习
在Rt△ABC 中,∠C=90°,AB=2,AC= ,则∠A 的度数为( )
A.90° B.60° C.45° D.30°
D
在△ABC 中,∠C=90°,AB=4,AC=3,欲求∠A的值,最适宜的做法是( )
A.计算tan A 的值求出 B.计算sin A 的值求出
C.计算cos A 的值求出
D.先根据sin B 求出∠B,再利用90°-∠B 求出
C
例3 如图,在 Rt△ABC 中,∠C = 90°,cosA = ,BC = 5, 试求 AB 的长.
A
C
B
解:
设
例4 如图,在△ABC 中,AB=1,AC=,sin B =,求BC 的长.
A
C
B
如图,过点A 作AD⊥BC 于点D.
∵AB=1,sin B=
∴AD=AB · sin B=
∴BD=
∴CD=
∴BC=CD+BD=
解:
知识小结
解直角三角形
定义
依据
思想
三边关系
三角关系
边与角关系
a2 + b2 =c2(勾股定理)
∠A +∠B =90°(两锐角互余定理)
三角函数
sinA = ,
cosA = ,
tanA =.
数形结合、方程思想
课堂练习
2. 如图,在 Rt△ABC 中,∠C = 90°,∠B = 30°, AB = 8,则 BC 的长是 ( )
D
1. 在 Rt△ABC 中,∠C = 90°,a,b,c 分别是∠A, ∠B,∠C 的对边,则下列各式正确的是 ( )
A. b = a·tanA B. b = c·sinA
C. b = c·cosA D. a = c·cosA
A
C
B
C
在 Rt△ABC 中,∠C = 90°,∠B = 37°,BC = 32, 则 AC = (参考数据:sin37° ≈ 0.60,cos37° ≈ 0.80,tan37° ≈ 0.75).
如图,已知 Rt△ABC 中,斜边 BC 上的高 AD = 3,cosB = ,则 AC 的长为 .
24
3.75
如图,在 Rt△ABC 中,∠C = 90°,AC = 6,角平分线 ,解这个直角三角形.
解:
∵ AD 平分∠BAC,
D
A
B
C
6
如图,已知 AC = 4,求 AB 和 BC 的长.
在 Rt△CDB 中,∠DCB =∠ACB-∠ACD = 45°,
解:如图,作 CD⊥AB 于点 D.
在 Rt△ACD 中,∵∠A = 30°,∴∠ACD = 90° - ∠A = 60°.
∴ BD = CD = 2.
D
解:过点 A 作 AD⊥BC 于点 D.
在△ACD 中,∠C = 45°,AC = 2,
∴ CD = AD = sinC · AC = 2sin45° = .
在△ABD 中,∠B = 30°,
∴ BD =
∴ BC = CD + BD =
如图,在△ABC 中,∠B = 30°,∠C = 45°,AC = 2,求 BC 的长.
D
A
B
C
在△ABC 中,AB = ,AC = 13,cosB = ,求 BC 的长.
图②
图①
解:∵cosB = ,∴∠B = 45°.
当△ABC 为钝角三角形时,如图①.
∵AC = 13,∴由勾股定理得 CD = 5.
∴BC = BD + CD = 12 + 5 = 17
当△ABC 为锐角三角形时,如图②,
此时 .BC = BD - CD = 12 - 5 = 7.
综上可知,BC 的长为 7 或 17.
图②
图①
如图,PB 为⊙O 的切线,B 为切点,过B 作OP 的垂线BA,垂足为C,交⊙O于点A,连接PA,AO.并延长AO 交⊙O 于点E,与PB 的延长线交于点D.
(1)求证:PA 是⊙O 的切线;
(2)若 ,且OC=4,求PA 的长和tan D 的值.
(1)证明:如图,连接BO,
∵PB 为⊙O 的切线,B 为切点,
∴OB⊥PD,∠PBO=90°.
又∵OA=OB,OC⊥AB,
∴∠AOC=∠BOC.
又∵OP=OP,
∴△PAO ≌ △PBO,
∴∠PAO=∠PBO=90°,
∴PA 是⊙O 的切线.
(2)解:∵∠ACO=∠PAO=90°,∠AOC=∠POA,
∴△AOC∽△POA,∴ .
又∵OC=4,∴AC=6.
在Rt△AOC 中,
OA= ,
∴PA=OA=3,又易知PA=PB,∴PB=3.
在Rt△PAO 中,
PO= =13.
如图,连接BE. ∵AE 为直径,∴∠ABE=90°.
又∵OC⊥AB,∴BE∥OP,
∴△DBE∽△DPO,BE=2OC=8.
∴ .
即 .解得BD .
∴在Rt△DBO 中,tan D= .
