28.2.2应用举例(第4课时)坡度课件 22张PPT 2022—2023学年人教版数学九年级下册
文档属性
| 名称 | 28.2.2应用举例(第4课时)坡度课件 22张PPT 2022—2023学年人教版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 25.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 20:58:03 | ||
图片预览







文档简介
(共22张PPT)
坡度问题
28.2 解直角三角形及其应用
| 28.2.2 应用举例 第4课时 |
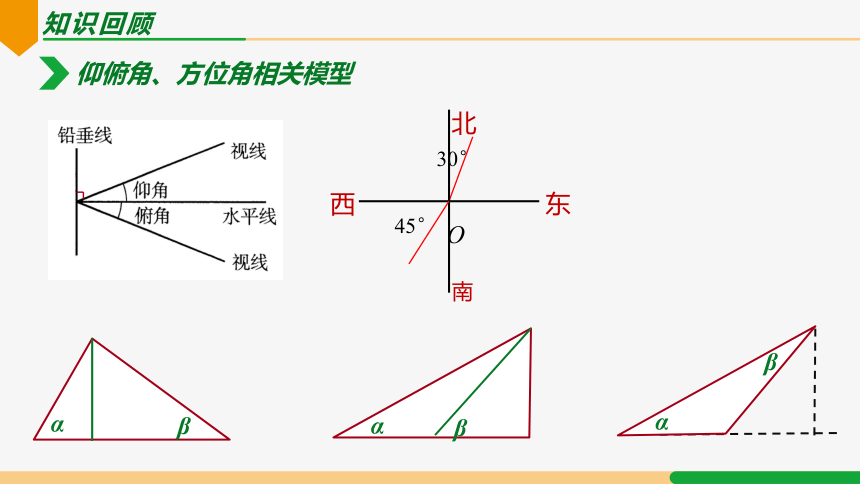
知识回顾
α
β
α
β
α
β
仰俯角、方位角相关模型
30°
45°
O
东
西
北
南
情景引入
从数学角底怎样描述山坡的陡峭
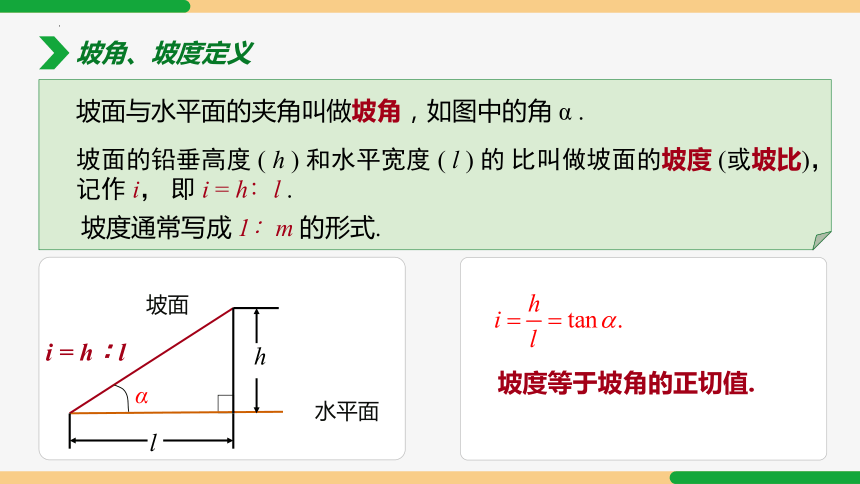
坡角、坡度定义
坡面与水平面的夹角叫做坡角,如图中的角 α .
坡度通常写成 1∶m 的形式.
坡面的铅垂高度 ( h ) 和水平宽度 ( l ) 的 比叫做坡面的坡度 (或坡比),记作 i, 即 i = h∶l .
α
l
h
i = h∶l
坡面
水平面
坡度等于坡角的正切值.
针对练习
1. 斜坡的坡度是 ,则坡角 α =____度.
2. 斜坡的坡角是 45°,则坡比是 _____.
3. 斜坡长是 12 米,坡高 6 米,则坡比是_______.
30
1 : 1
α
l
h
典例讲解
例1 如图,一山坡的坡度为 i = 1∶2. 小刚从山脚 A出发,沿山坡向上走了 240 m 到达点 C. 这座山坡的坡角是多少度?小刚上升了多少米(角度精确到0.01°,长度精确到 0.1 m)?
i = 1:2
A
B
C
在 Rt△ABC 中,
∠B = 90°,∠A ≈ 26.57°,AC = 240 m,
解:
用 α 表示坡角的大小,由题意可得
因此 α ≈ 26.57°.
答:这座山坡的坡角约为 26.57°,小刚上升了约 107.3 m.
从而 BC ≈ 240 sin26.57° ≈ 107.3 (m).
因此
A
B
C
i = 1:2
例2 如图,水库大坝的横断面是梯形,坝顶宽 6 m,坝高 23 m,斜坡 AB 的坡度 i = 1∶3,斜坡 CD 的坡度 i = 1∶2.5,求:
(1) 斜坡 CD 的坡角 α (精确到 1°);
(2) 坝底 AD 与斜坡 AB 的长度 (精确到 0.1m).
A
D
B
C
i = 1:2.5
23
6
α
i = 1:3
解: 斜坡 CD 的坡度
i = tanα = 1∶2.5 = 0.4,
由计算器可求得 α ≈ 22°.
故斜坡 CD 的坡角 α 约为 22°.
解:分别过点 B,C 作 BE⊥AD 于 E,CF⊥AD 于 F. 由题意可知 BE = CF = 23 m, EF = BC = 6 m.
在 Rt△ABE 中,
(2) 坝底 AD 与斜坡 AB 的长度 (精确到 0.1m).
E
F
A
D
B
C
i = 1:2.5
23
6
α
i = 1:3
∴ AD=AE+EF+FD
= 69 + 6 + 57.5 = 132.5 (m).
在Rt△ABE中,由勾股定理可得
在 Rt△DCF 中,
故坝底 AD 的长度为132.5 m,斜坡 AB 的长度为 72.7 m.
∵ FD=2.5CF=2.5×23=57.5(m)
针对练习
为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是:水坝加高2米(即CD=2米),背水坡DE 的坡度i=1∶1(即DB∶EB=1∶1),如图所示,已知AE=4米,∠EAC=130°,求水坝原来的高度B C. (参考数据:sin 50°≈0.77,cos 50°≈0.64,tan 50°≈1.2)
解:
设BC=x,
在Rt△ABC 中,∠CAB=180°-∠EAC=50°,
∴AB===x
在Rt△EBD 中,i=DB∶EB=1∶1,
∴BD=BE. ∴CD+BC=AE+AB,
即2+x=4+x,解得x=12.
答:水坝原来的高度约为12米.
知识小结
坡面与水平面的夹角叫做坡角,如图中的角 α .
坡度通常写成 1∶m 的形式.
坡面的铅垂高度 ( h ) 和水平宽度 ( l ) 的 比叫做坡面的坡度 (或坡比),记作 i, 即 i = h∶l .
α
l
h
i = h∶l
坡面
水平面
坡度等于坡角的正切值.
课堂练习
如图,河坝横断面迎水坡AB的坡比是1 : ,坝高 BC = 3 m,则坡面 AB 的长度是 ( )
A. 9 m B. 6 m C. m D. m
A
C
B
B
如图,小王在长江边某瞭望台D 处,测得江面上的渔船A 的俯角为40°,若DE=3米,CE=2米,CE 平行于江面AB,迎水坡BC 的坡度i=1∶0.75,坡长BC=10米,则此时AB 的长约为( )
(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)
A.5.1米 B.6.3米
C.7.1米 D.9.2米
A
如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了________米.(参考数据:sin 34°≈0.56,cos 34°≈0.83,tan 34°≈0.67)
280
为加强防汛工作,某市对一拦水坝进行加固.如图,加固前拦水坝的横断面是梯形ABCD. 已知迎水坡面AB=12米,背水坡面CD=123米,∠B=60°,加固后拦水坝的横断面为梯形ABED,tan E=,则CE 的长为________米.
8
一段路基的横断面是梯形,高为 4 米,上底的宽是 12 米,路基左右两边坡面的坡角分别是 45° 和 30°,求路基下底的宽 (精确到 0.01米,,).
45°
30°
4 米
12 米
A
B
C
D
E
F
解:如图,作DE⊥AB 于 E,CF⊥AB 于 F.
由题意知 DE=CF=4 (米),CD=EF=12 (米).
45°
30°
4 米
12 米
A
B
C
D
在 Rt△ADE 中,
E
F
在 Rt△BCF 中,同理可得
∴ AB=AE+EF+BF ≈ 4+12+6.93 = 22.93 (米).
答: 路基下底的宽约为 22.93 米.
(米).
(米).
一个长方体木箱沿斜面下滑,当木箱滑至如图所示的位置时,AB=3 m,已知木箱高BE=m,斜面坡角为30°,求木箱端点E 距地面AC 的高度EF.
解:如图,连接AE.
在Rt△ABE 中,AB=3,BE=,
则AE==
∵tan ∠EAB= = ∴∠EAB=30°.
在Rt△AEF 中,∠EAF=∠EAB+∠BAC
=30°+30°=60°,
∴EF=AE × sin ∠EAF==3
答:木箱端点E 距地面AC 的高度EF 为3 m.
如图,某校教学楼AB 后方有一斜坡,已知斜坡CD 的长为12米,坡角α 为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD 进行改造,在保持坡脚C 不动的情况下,学校至少要把坡顶D 向后水平移动多少米才能保证教学楼的安全?(结果取整数,参考数据:sin 39°≈0.63, cos 39°≈0.78,tan39°≈0.81, ≈1.41, ≈1.73, ≈2.24)
假设点D 移到D ′的位置时,恰好∠α=39°,过点D 作DE⊥AC 于点E,过点D ′作D ′E ′⊥AC 于点E ′,如图所示.
∵CD=12,∠DCE=60°,
∴DE=CD ·sin 60°=12× =6,
CE=CD · cos 60°=12× =6.
∵DE⊥AC,D ′E ′⊥AC,DD ′∥CE ′,
∴四边形DEE ′D ′是矩形.∴D ′E ′=DE=6.
∵∠D ′CE ′=39°,∴CE ′=≈≈12.8.
∴EE ′=CE ′-CE=12.8-6=6.8≈7(米).
答:学校至少要把坡顶D 向后水平移动7米才能保证教学楼的安全.
解:
坡度问题
28.2 解直角三角形及其应用
| 28.2.2 应用举例 第4课时 |
知识回顾
α
β
α
β
α
β
仰俯角、方位角相关模型
30°
45°
O
东
西
北
南
情景引入
从数学角底怎样描述山坡的陡峭
坡角、坡度定义
坡面与水平面的夹角叫做坡角,如图中的角 α .
坡度通常写成 1∶m 的形式.
坡面的铅垂高度 ( h ) 和水平宽度 ( l ) 的 比叫做坡面的坡度 (或坡比),记作 i, 即 i = h∶l .
α
l
h
i = h∶l
坡面
水平面
坡度等于坡角的正切值.
针对练习
1. 斜坡的坡度是 ,则坡角 α =____度.
2. 斜坡的坡角是 45°,则坡比是 _____.
3. 斜坡长是 12 米,坡高 6 米,则坡比是_______.
30
1 : 1
α
l
h
典例讲解
例1 如图,一山坡的坡度为 i = 1∶2. 小刚从山脚 A出发,沿山坡向上走了 240 m 到达点 C. 这座山坡的坡角是多少度?小刚上升了多少米(角度精确到0.01°,长度精确到 0.1 m)?
i = 1:2
A
B
C
在 Rt△ABC 中,
∠B = 90°,∠A ≈ 26.57°,AC = 240 m,
解:
用 α 表示坡角的大小,由题意可得
因此 α ≈ 26.57°.
答:这座山坡的坡角约为 26.57°,小刚上升了约 107.3 m.
从而 BC ≈ 240 sin26.57° ≈ 107.3 (m).
因此
A
B
C
i = 1:2
例2 如图,水库大坝的横断面是梯形,坝顶宽 6 m,坝高 23 m,斜坡 AB 的坡度 i = 1∶3,斜坡 CD 的坡度 i = 1∶2.5,求:
(1) 斜坡 CD 的坡角 α (精确到 1°);
(2) 坝底 AD 与斜坡 AB 的长度 (精确到 0.1m).
A
D
B
C
i = 1:2.5
23
6
α
i = 1:3
解: 斜坡 CD 的坡度
i = tanα = 1∶2.5 = 0.4,
由计算器可求得 α ≈ 22°.
故斜坡 CD 的坡角 α 约为 22°.
解:分别过点 B,C 作 BE⊥AD 于 E,CF⊥AD 于 F. 由题意可知 BE = CF = 23 m, EF = BC = 6 m.
在 Rt△ABE 中,
(2) 坝底 AD 与斜坡 AB 的长度 (精确到 0.1m).
E
F
A
D
B
C
i = 1:2.5
23
6
α
i = 1:3
∴ AD=AE+EF+FD
= 69 + 6 + 57.5 = 132.5 (m).
在Rt△ABE中,由勾股定理可得
在 Rt△DCF 中,
故坝底 AD 的长度为132.5 m,斜坡 AB 的长度为 72.7 m.
∵ FD=2.5CF=2.5×23=57.5(m)
针对练习
为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是:水坝加高2米(即CD=2米),背水坡DE 的坡度i=1∶1(即DB∶EB=1∶1),如图所示,已知AE=4米,∠EAC=130°,求水坝原来的高度B C. (参考数据:sin 50°≈0.77,cos 50°≈0.64,tan 50°≈1.2)
解:
设BC=x,
在Rt△ABC 中,∠CAB=180°-∠EAC=50°,
∴AB===x
在Rt△EBD 中,i=DB∶EB=1∶1,
∴BD=BE. ∴CD+BC=AE+AB,
即2+x=4+x,解得x=12.
答:水坝原来的高度约为12米.
知识小结
坡面与水平面的夹角叫做坡角,如图中的角 α .
坡度通常写成 1∶m 的形式.
坡面的铅垂高度 ( h ) 和水平宽度 ( l ) 的 比叫做坡面的坡度 (或坡比),记作 i, 即 i = h∶l .
α
l
h
i = h∶l
坡面
水平面
坡度等于坡角的正切值.
课堂练习
如图,河坝横断面迎水坡AB的坡比是1 : ,坝高 BC = 3 m,则坡面 AB 的长度是 ( )
A. 9 m B. 6 m C. m D. m
A
C
B
B
如图,小王在长江边某瞭望台D 处,测得江面上的渔船A 的俯角为40°,若DE=3米,CE=2米,CE 平行于江面AB,迎水坡BC 的坡度i=1∶0.75,坡长BC=10米,则此时AB 的长约为( )
(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)
A.5.1米 B.6.3米
C.7.1米 D.9.2米
A
如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了________米.(参考数据:sin 34°≈0.56,cos 34°≈0.83,tan 34°≈0.67)
280
为加强防汛工作,某市对一拦水坝进行加固.如图,加固前拦水坝的横断面是梯形ABCD. 已知迎水坡面AB=12米,背水坡面CD=123米,∠B=60°,加固后拦水坝的横断面为梯形ABED,tan E=,则CE 的长为________米.
8
一段路基的横断面是梯形,高为 4 米,上底的宽是 12 米,路基左右两边坡面的坡角分别是 45° 和 30°,求路基下底的宽 (精确到 0.01米,,).
45°
30°
4 米
12 米
A
B
C
D
E
F
解:如图,作DE⊥AB 于 E,CF⊥AB 于 F.
由题意知 DE=CF=4 (米),CD=EF=12 (米).
45°
30°
4 米
12 米
A
B
C
D
在 Rt△ADE 中,
E
F
在 Rt△BCF 中,同理可得
∴ AB=AE+EF+BF ≈ 4+12+6.93 = 22.93 (米).
答: 路基下底的宽约为 22.93 米.
(米).
(米).
一个长方体木箱沿斜面下滑,当木箱滑至如图所示的位置时,AB=3 m,已知木箱高BE=m,斜面坡角为30°,求木箱端点E 距地面AC 的高度EF.
解:如图,连接AE.
在Rt△ABE 中,AB=3,BE=,
则AE==
∵tan ∠EAB= = ∴∠EAB=30°.
在Rt△AEF 中,∠EAF=∠EAB+∠BAC
=30°+30°=60°,
∴EF=AE × sin ∠EAF==3
答:木箱端点E 距地面AC 的高度EF 为3 m.
如图,某校教学楼AB 后方有一斜坡,已知斜坡CD 的长为12米,坡角α 为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD 进行改造,在保持坡脚C 不动的情况下,学校至少要把坡顶D 向后水平移动多少米才能保证教学楼的安全?(结果取整数,参考数据:sin 39°≈0.63, cos 39°≈0.78,tan39°≈0.81, ≈1.41, ≈1.73, ≈2.24)
假设点D 移到D ′的位置时,恰好∠α=39°,过点D 作DE⊥AC 于点E,过点D ′作D ′E ′⊥AC 于点E ′,如图所示.
∵CD=12,∠DCE=60°,
∴DE=CD ·sin 60°=12× =6,
CE=CD · cos 60°=12× =6.
∵DE⊥AC,D ′E ′⊥AC,DD ′∥CE ′,
∴四边形DEE ′D ′是矩形.∴D ′E ′=DE=6.
∵∠D ′CE ′=39°,∴CE ′=≈≈12.8.
∴EE ′=CE ′-CE=12.8-6=6.8≈7(米).
答:学校至少要把坡顶D 向后水平移动7米才能保证教学楼的安全.
解:
