28.2.2应用举例第3课时(方位角)课件 19张PPT 2022—2023学年人教版数学九年级下册
文档属性
| 名称 | 28.2.2应用举例第3课时(方位角)课件 19张PPT 2022—2023学年人教版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 24.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 21:05:47 | ||
图片预览




文档简介
(共19张PPT)
方位角问题
28.2 解直角三角形及其应用
| 28.2.2 应用举例 第3课时 |
知识导航
解直角三角形能解决那些实际问题?
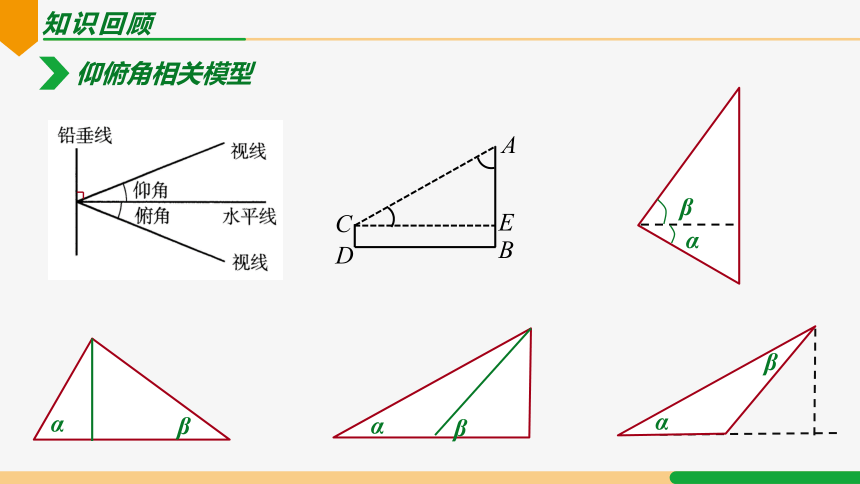
知识回顾
A
D
B
E
C
α
β
α
β
α
β
α
β
仰俯角相关模型
典例讲解
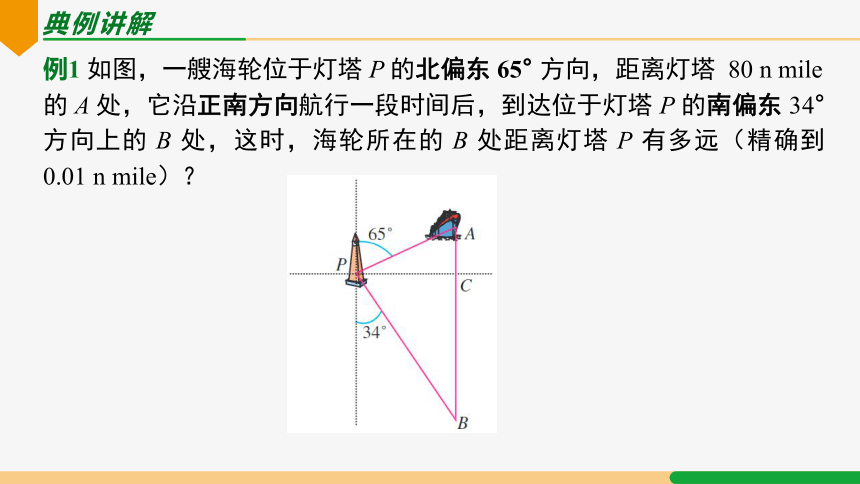
例1 如图,一艘海轮位于灯塔 P 的北偏东 65° 方向,距离灯塔 80 n mile 的 A 处,它沿正南方向航行一段时间后,到达位于灯塔 P 的南偏东 34° 方向上的 B 处,这时,海轮所在的 B 处距离灯塔 P 有多远(精确到 0.01 n mile)?
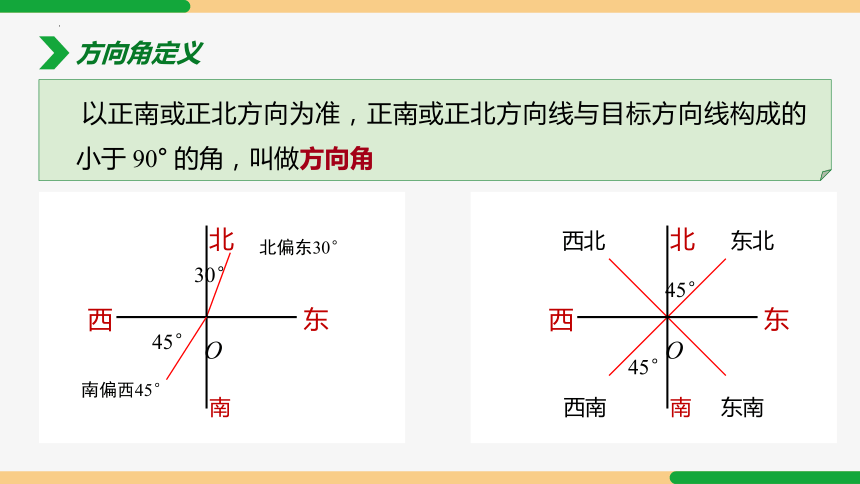
方向角定义
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于 90° 的角,叫做方向角
北偏东30°
南偏西45°
30°
45°
O
东
西
北
南
45°
45°
西南
O
东北
东
西
北
南
西北
东南
解:如图,在 Rt△APC 中,
PC = PA·cos(90°-65°)
= 80×cos25°
≈ 72.505.
在 Rt△BPC 中,∠B = 34°,
因此,当海轮到达位于灯塔P的南偏东 34° 方向时,它距离灯塔 P 大约 129.66 n mile.
例2 如图,A,B 两城市相距 200 km. 现计划在这两座城市间修筑一条高速公路 (即线段 AB),经测量,森林保护中心 P 在 A 城市的北偏东 30° 和 B 城市的北偏西 45° 的方向上.已知森林保护区的范围在以 P 点为圆心,100 km 为半径的圆形区域内,请问:计划修筑的这条高速公路会不会穿越保护区(参考数据:≈1.732,≈1.414)?
解:过点 P 作 PC⊥AB 于点 C,
则∠APC=30°,∠BPC=45°,
AC=PC·tan30°,BC=PC·tan45°.
∵ AC+BC=AB,
∴ PC·tan30°+PC·tan45°=200,
即 PC+PC=200,
解得 PC ≈ 126.8 km>100 km.
答:计划修筑的这条高速公路不会穿越保护区.
200 km
C
例3 如图,海岛 A 的周围 8 海里内有暗礁,渔船跟踪鱼群由西向东航行,在点 B 处测得海岛 A 位于北偏东 60°,航行 12 海里到达点 C 处,又测得海岛 A 位于北偏东 30°,如果渔船不改变航向继续向东航行,有没有触礁的危险?
北
东
A
C
B
60°
30°
D
∵ BD∥CE∥AF,
∴∠DBA =∠BAF = 60°,∠ACE =∠CAF = 30°.
∴∠BAC =∠BAF-∠CAF = 60°-30° = 30°.
又∵∠ABC =∠DBF-∠DBA = 90°-60° = 30° =∠BAC,
∴∠ABC =∠BAC,
∴ BC = AC = 12 海里.
∴ AF = AC · cos30° = 6 ≈ 10.392 > 8,
故渔船继续向正东方向行驶,没有触礁的危险.
北
东
A
C
B
60°
30°
D
E
F
例4 如图,港口B 位于港口A 的南偏东37°方向,灯塔C 恰好在AB 的中点处,一艘海轮位于港口A 的正南方向,港口B 的正西方向的D 处,它沿正北方向航行5 km到达E 处,测得灯塔C 在北偏东45°方向上,这时,E 处距离港口A 有多远?(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
如图,作CH⊥AD于点H. 设CH=x,
在Rt△ACH 中,∠A=37°, tan 37°= ,
∴ AH== .
在Rt△CEH 中,
∵∠CEH=45°, ∴CH=EH=x.
∵ CH⊥AD,BD⊥AD, ∴CH∥BD,
∴ .
∵AC=CB,∴AH=HD.
∴ =x+5. ∴ x≈15.
∴AE=AH+HE= +15≈35(km),
∴E 处距离港口A 约35 km.
解:
知识小结
α
β
α
β
α
β
α
β
方位角相关模型
30°
45°
O
东
西
北
南
课堂练习
如图,一艘海轮位于灯塔P 的北偏东55°方向,距离灯塔2海里的A处.如果海轮沿正南方向航行到灯塔的正东位置,则海轮航行的距离AB 是( )
A.2海里 B.2sin 55°海里
C.2cos 55°海里 D.2tan 55°海里
C
如图,一艘轮船在A 处测得灯塔P 位于其北偏东60°方向上,轮船沿正东方向航行30海里到达B 处后,此时测得灯塔P 位于其北偏东30°方向上,此时轮船与灯塔P 的距离是( )
A.15海里 B.30海里
C.45海里 D.30海里
B
如图,有一个古建筑 A,它周围 800 米内有古建筑群,乡村路要由西向东修筑,在 B 点处测得古建筑 A 在北偏东 60° 方向上,向前直行 1200 米到达 D 点,这时测得古建筑 A 在 D 点北偏东 30° 方向上,如果不改变修筑的方向,你认为古建筑群会不会遭到破坏?
解:过点 A 作 AE⊥BD,垂足为 E.
∵ 点 A 在点 B 的北偏东 60° 方向上,在点 D 的北偏东 30° 方向上,
∴ ∠ABE = 30°,∠ADE = 60°.
∴∠BAD =∠ADE -∠ABE = 30° =∠ABE.
∴ AD = BD = 1200 米.
∴ AE = AD·sin60° = 1200× ≈ 1039.2>800(米).
∴ 不会遭到破坏.
E
如图,一艘轮船位于灯塔P 南偏西60°方向的A 处,它向东 航行20海里到达灯塔P 南偏西45°方向上的B 处,若轮船继续沿正东方向航行,求轮船航行途中与灯塔P 的最短离.(结果保留根号)
解:
如图,作PC⊥AB 交AB 的延长线于点C,
则∠APC=60°,∠BPC=45°,AB=20.
∴PC=BC,
AC=PC · tan 60°=PC.
∴AB=AC-BC=(-1)·PC=20.
∴PC= =10+10(海里).
答:轮船航行途中与灯塔P 的最短距离是(10 +10)海里.
方位角问题
28.2 解直角三角形及其应用
| 28.2.2 应用举例 第3课时 |
知识导航
解直角三角形能解决那些实际问题?
知识回顾
A
D
B
E
C
α
β
α
β
α
β
α
β
仰俯角相关模型
典例讲解
例1 如图,一艘海轮位于灯塔 P 的北偏东 65° 方向,距离灯塔 80 n mile 的 A 处,它沿正南方向航行一段时间后,到达位于灯塔 P 的南偏东 34° 方向上的 B 处,这时,海轮所在的 B 处距离灯塔 P 有多远(精确到 0.01 n mile)?
方向角定义
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于 90° 的角,叫做方向角
北偏东30°
南偏西45°
30°
45°
O
东
西
北
南
45°
45°
西南
O
东北
东
西
北
南
西北
东南
解:如图,在 Rt△APC 中,
PC = PA·cos(90°-65°)
= 80×cos25°
≈ 72.505.
在 Rt△BPC 中,∠B = 34°,
因此,当海轮到达位于灯塔P的南偏东 34° 方向时,它距离灯塔 P 大约 129.66 n mile.
例2 如图,A,B 两城市相距 200 km. 现计划在这两座城市间修筑一条高速公路 (即线段 AB),经测量,森林保护中心 P 在 A 城市的北偏东 30° 和 B 城市的北偏西 45° 的方向上.已知森林保护区的范围在以 P 点为圆心,100 km 为半径的圆形区域内,请问:计划修筑的这条高速公路会不会穿越保护区(参考数据:≈1.732,≈1.414)?
解:过点 P 作 PC⊥AB 于点 C,
则∠APC=30°,∠BPC=45°,
AC=PC·tan30°,BC=PC·tan45°.
∵ AC+BC=AB,
∴ PC·tan30°+PC·tan45°=200,
即 PC+PC=200,
解得 PC ≈ 126.8 km>100 km.
答:计划修筑的这条高速公路不会穿越保护区.
200 km
C
例3 如图,海岛 A 的周围 8 海里内有暗礁,渔船跟踪鱼群由西向东航行,在点 B 处测得海岛 A 位于北偏东 60°,航行 12 海里到达点 C 处,又测得海岛 A 位于北偏东 30°,如果渔船不改变航向继续向东航行,有没有触礁的危险?
北
东
A
C
B
60°
30°
D
∵ BD∥CE∥AF,
∴∠DBA =∠BAF = 60°,∠ACE =∠CAF = 30°.
∴∠BAC =∠BAF-∠CAF = 60°-30° = 30°.
又∵∠ABC =∠DBF-∠DBA = 90°-60° = 30° =∠BAC,
∴∠ABC =∠BAC,
∴ BC = AC = 12 海里.
∴ AF = AC · cos30° = 6 ≈ 10.392 > 8,
故渔船继续向正东方向行驶,没有触礁的危险.
北
东
A
C
B
60°
30°
D
E
F
例4 如图,港口B 位于港口A 的南偏东37°方向,灯塔C 恰好在AB 的中点处,一艘海轮位于港口A 的正南方向,港口B 的正西方向的D 处,它沿正北方向航行5 km到达E 处,测得灯塔C 在北偏东45°方向上,这时,E 处距离港口A 有多远?(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
如图,作CH⊥AD于点H. 设CH=x,
在Rt△ACH 中,∠A=37°, tan 37°= ,
∴ AH== .
在Rt△CEH 中,
∵∠CEH=45°, ∴CH=EH=x.
∵ CH⊥AD,BD⊥AD, ∴CH∥BD,
∴ .
∵AC=CB,∴AH=HD.
∴ =x+5. ∴ x≈15.
∴AE=AH+HE= +15≈35(km),
∴E 处距离港口A 约35 km.
解:
知识小结
α
β
α
β
α
β
α
β
方位角相关模型
30°
45°
O
东
西
北
南
课堂练习
如图,一艘海轮位于灯塔P 的北偏东55°方向,距离灯塔2海里的A处.如果海轮沿正南方向航行到灯塔的正东位置,则海轮航行的距离AB 是( )
A.2海里 B.2sin 55°海里
C.2cos 55°海里 D.2tan 55°海里
C
如图,一艘轮船在A 处测得灯塔P 位于其北偏东60°方向上,轮船沿正东方向航行30海里到达B 处后,此时测得灯塔P 位于其北偏东30°方向上,此时轮船与灯塔P 的距离是( )
A.15海里 B.30海里
C.45海里 D.30海里
B
如图,有一个古建筑 A,它周围 800 米内有古建筑群,乡村路要由西向东修筑,在 B 点处测得古建筑 A 在北偏东 60° 方向上,向前直行 1200 米到达 D 点,这时测得古建筑 A 在 D 点北偏东 30° 方向上,如果不改变修筑的方向,你认为古建筑群会不会遭到破坏?
解:过点 A 作 AE⊥BD,垂足为 E.
∵ 点 A 在点 B 的北偏东 60° 方向上,在点 D 的北偏东 30° 方向上,
∴ ∠ABE = 30°,∠ADE = 60°.
∴∠BAD =∠ADE -∠ABE = 30° =∠ABE.
∴ AD = BD = 1200 米.
∴ AE = AD·sin60° = 1200× ≈ 1039.2>800(米).
∴ 不会遭到破坏.
E
如图,一艘轮船位于灯塔P 南偏西60°方向的A 处,它向东 航行20海里到达灯塔P 南偏西45°方向上的B 处,若轮船继续沿正东方向航行,求轮船航行途中与灯塔P 的最短离.(结果保留根号)
解:
如图,作PC⊥AB 交AB 的延长线于点C,
则∠APC=60°,∠BPC=45°,AB=20.
∴PC=BC,
AC=PC · tan 60°=PC.
∴AB=AC-BC=(-1)·PC=20.
∴PC= =10+10(海里).
答:轮船航行途中与灯塔P 的最短距离是(10 +10)海里.
