2023-2024学年沪教版(上海)七年级上册第十一章图形的运动单元测试卷(含解析)
文档属性
| 名称 | 2023-2024学年沪教版(上海)七年级上册第十一章图形的运动单元测试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 807.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 09:42:14 | ||
图片预览


文档简介
2023-2024学年 沪教版(上海)七年级上册 第十一章 图形的运动 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.中国“二十四节气”已被列入联合国教科文组织人类非物质文化遗产代表作名录,下列四幅作品分别代 表“大雪”、“白露”、“芒种”、“立春”,其中是轴对称图形的是( )
A. B. C. D.
2.下列图标中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
3.2023年秋季,19届亚运会在杭州如火如荼地进行,运动健儿们摘金夺银,全国人民感受到一波强烈的民族自豪感.下列图案表示的运动项目标志中,是轴对称图形的是( )
A. B. C. D.
4.如图,在正方形网格中,绕某一点旋转某一角度得到,则旋转中心可能是( )
A.点A B.点B C.点C D.点D
5.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
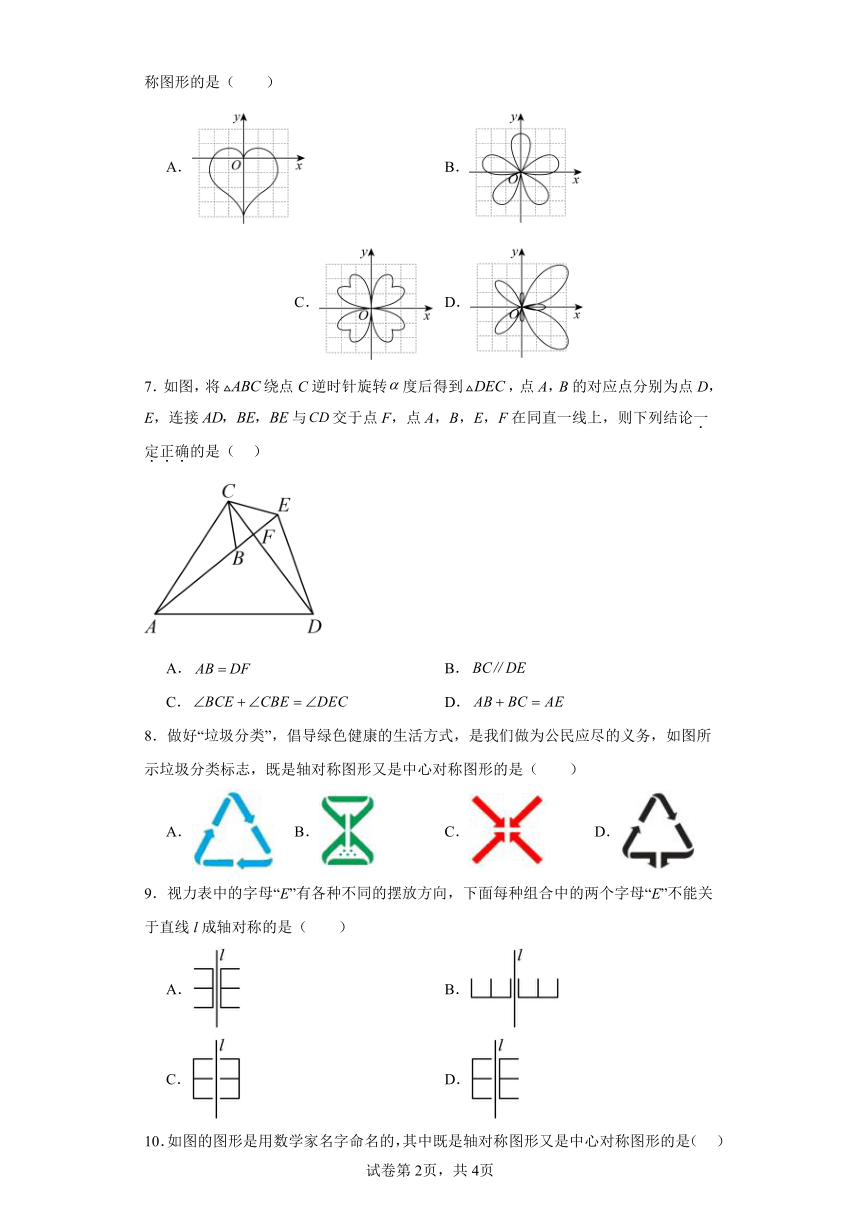
6.下列各曲线是在平面直角坐标系中根据不同的方程绘制而成的,其中是中心对称图形的是( )
A. B. C. D.
7.如图,将绕点C逆时针旋转度后得到,点A,B的对应点分别为点D,E,连接与交于点F,点A,B,E,F在同直一线上,则下列结论一定正确的是( )
A. B.
C. D.
8.做好“垃圾分类”,倡导绿色健康的生活方式,是我们做为公民应尽的义务,如图所示垃圾分类标志,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
9.视力表中的字母“E”有各种不同的摆放方向,下面每种组合中的两个字母“E”不能关于直线l成轴对称的是( )
A. B.
C. D.
10.如图的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )
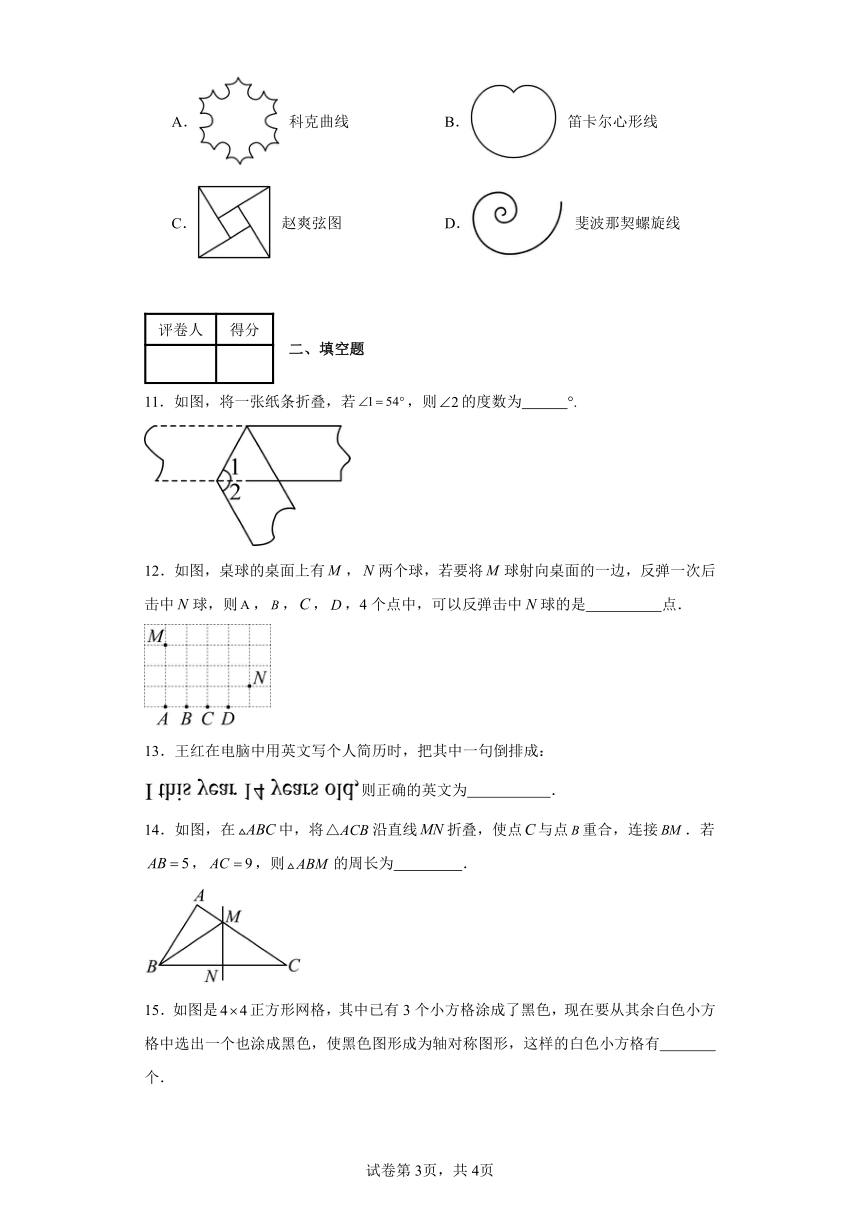
A. 科克曲线 B. 笛卡尔心形线
C. 赵爽弦图 D. 斐波那契螺旋线
评卷人得分
二、填空题
11.如图,将一张纸条折叠,若,则的度数为 °.
12.如图,桌球的桌面上有,两个球,若要将球射向桌面的一边,反弹一次后击中球,则,,,,4个点中,可以反弹击中球的是 点.
13.王红在电脑中用英文写个人简历时,把其中一句倒排成:则正确的英文为 .
14.如图,在中,将沿直线折叠,使点与点重合,连接.若,,则的周长为 .
15.如图是正方形网格,其中已有3个小方格涂成了黑色,现在要从其余白色小方格中选出一个也涂成黑色,使黑色图形成为轴对称图形,这样的白色小方格有 个.
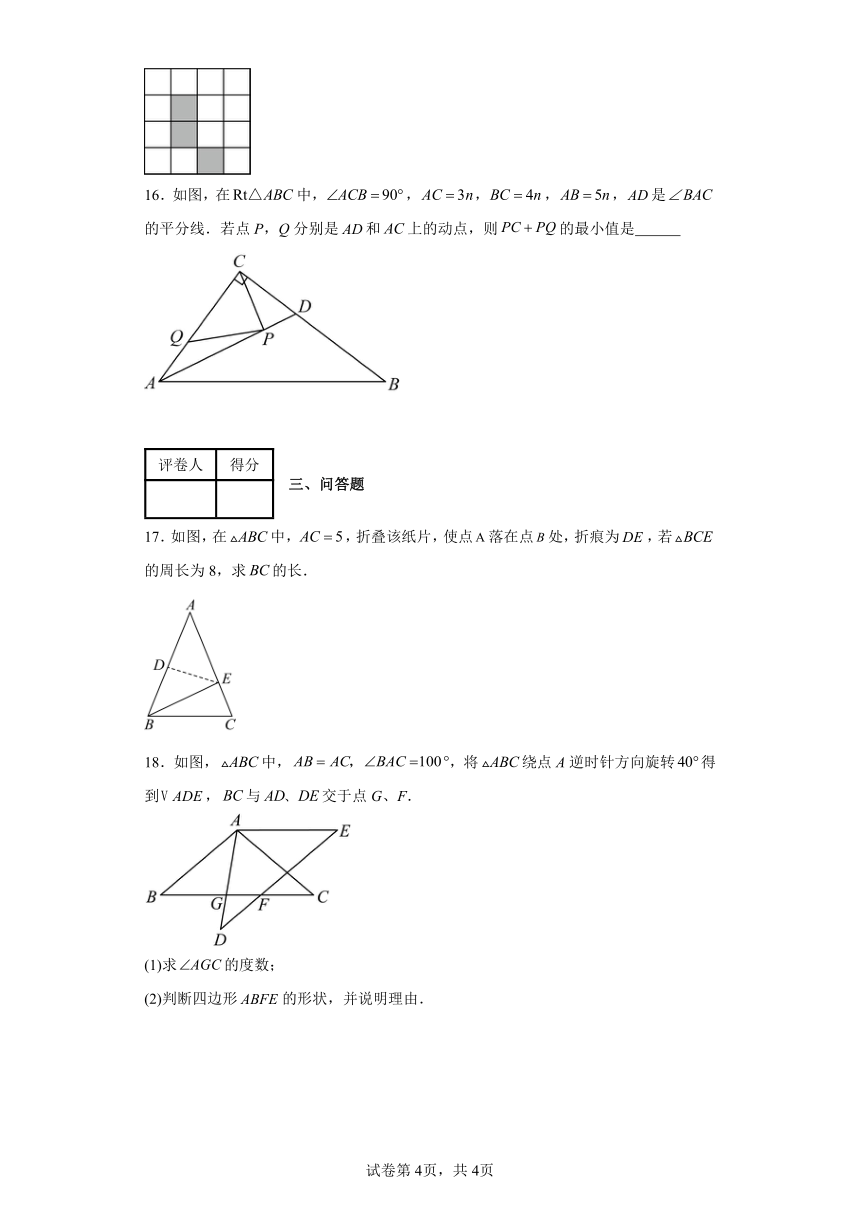
16.如图,在中,,,,,是的平分线.若点P,Q分别是和上的动点,则的最小值是
评卷人得分
三、问答题
17.如图,在中,,折叠该纸片,使点落在点处,折痕为,若的周长为8,求的长.
18.如图,中,,将绕点A逆时针方向旋转得到,与交于点G、F.
(1)求的度数;
(2)判断四边形的形状,并说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】本题考查了轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合.根据轴对称图形的知识求解.
【详解】解:A、是轴对称图形,故本选项符合题意;
B、不是轴对称图形,故本选项不符合题意;
C、不是轴对称图形,故本选项不符合题意;
D、不是轴对称图形,故本选项不符合题意.
故选:A.
2.C
【分析】中心对称图形定义:把一个图形绕着某个点旋转,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形;轴对称图形定义:如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形,根据定义逐项判断即可得出结论.本题考查中心对称图形与轴对称图形,熟练掌握中心对称图形与轴对称图形的定义是解决问题的关键.
【详解】解:A、不是轴对称图形,是中心对称图形,故选项不符合题意;
B、不是轴对称图形,不是中心对称图形,故选项不符合题意;
C、既是轴对称图形,又是中心对称图形,故选项符合题意;
D、是轴对称图形,不是中心对称图形,故选项不符合题意;
故选:C.
3.B
【分析】本题考查的是轴对称图形的识别.根据一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
【详解】解:A.不是轴对称图形,不符合题意;
B.是轴对称图形,符合题意;
C.不是轴对称图形,不符合题意;
D.不是轴对称图形,不符合题意;
故选:B.
4.B
【分析】如图:连接,作的垂直平分线,作的垂直平分线,两垂直平分线的交点即为旋转中心;掌握旋转中心的确定方法是解题的关键.
【详解】解:如图,
∵绕某点旋转一定的角度,得到,
∴连接,作的垂直平分线,作的垂直平分线,
∴三条线段的垂直平分线正好都过B,即旋转中心是B.
故选:B.
5.B
【分析】本题考查了中心对称图形与轴对称图形,根据轴对称图形和中心对称图形的定义进行逐一判断即可:如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形;把一个图形绕着某一个点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.掌握中心对称图形与轴对称图形的判断是解题的关键.
【详解】解:A、是中心对称图形,但不是轴对称图形,故不符合题意;
B、既是轴对称图形,也是中心对称图形,故符合题意;
C、是轴对称图形,但不是中心对称图形,故不符合题意;
D、不是轴对称图形,也不是中心对称图形,故符合题意.
故选:B.
6.C
【分析】本题主要是考查了中心对称图形的定义,熟练掌握中心对图形的定义“旋转180°能与自身重合的图形即为中心对称图形”,是解决该题的关键.
【详解】解:解:A、不是中心对称图形,故A错误.
B、不是中心对称图形,故B错误.
C、是中心对称图形,故C正确.
D、不是中心对称图形,故D错误.
故选:C.
7.C
【分析】根据旋转的性质和反证法进行证明即可得到答案.熟练掌握反证法是解题的关键.
【详解】解:解:A.∵将绕点C逆时针旋转度后得到,
∴,
但无法确定,故选项错误,不符合题意;
B.∵将绕点C逆时针旋转度后得到,
∴,
∴,,
若,则,
∴,
∴,
∴,
∴是等边三角形,
∴,
∴,
∵大小未知,
故选项错误,不符合题意;
C.∵将绕点C逆时针旋转度后得到,
∴,
∴,
∵,
∴,
∴,
故选项正确,符合题意;
D.∵将绕点C逆时针旋转度后得到,
∴,
若,
∵,
∴,
即是等边三角形,
当且仅当时成立,
故选项错误,不符合题意.
故选:C.
8.C
【分析】本题考查了轴对称图形和中心对称图形的识别,根据轴对称图形的定义:平面内,一个图形沿一条直线折叠 ,直线两旁的部分能够完全重合的图形,中心对称图形的定义:把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,据此逐项判断即可.
【详解】解:A、该图形既不是轴对称图形,也不是中心对称图形,本项不符合题意;
B、该图形是轴对称图形,但不是中心对称图形,本项不符合题意;
C、该图形既是轴对称图形,也是中心对称图形,本项符合题意;
D、该图形不是轴对称图形,也不是中心对称图形,本项不符合题意;
故答案为:C.
9.D
【分析】本题主要考查了轴对称的图形,根据轴对称图形的定义解题即可.
【详解】解:A、两个字母“E”关于直线l成轴对称,故本选项不符合题意;
B、两个字母“E”关于直线l成轴对称,故本选项不符合题意;
C、两个字母“E”关于直线l成轴对称,故本选项不符合题意;
D、两个字母“E”不能沿着直线 l翻折互相重合,故本选项符合题意.
故选:D.
10.A
【分析】本题考查了中心对称图形与轴对称图形,根据轴对称图形和中心对称图形的定义进行逐一判断即可:如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形;把一个图形绕着某一个点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.掌握中心对称图形与轴对称图形的判断是解题的关键.
【详解】解:A、既是轴对称图形,也是中心对称图形,故符合题意;
B、是轴对称图形,但不是中心对称图形,故不符合题意;
C、不是轴对称图形,是中心对称图形,故不符合题意;
D、既不是轴对称图形,也不是中心对称图形,故符合题意;
故选:A.
11.
【分析】根据折叠的性质即可得出关于的一元一次方程,解之即可得出结论.本题考查角的计算以及折叠的性质,解题的关键是明确题意,掌握折叠前后的对应角相等的性质.
【详解】解: 根据折叠的性质可知:,
即,
解得:.
故答案为:.
12.D
【分析】本题考查了轴对称的性质,解题关键是根据轴对称的性质找到使入射角等于反射角相等的点.
【详解】解:如图,根据轴对称的性质可知,可以反弹击中球的是D点,
故选:D.
13.
【分析】本题是镜面反射的知识,可以在这句话的正上方放一面镜子,看镜子里的字母就可以了.
【详解】解:如图在这句话的正上方放一面镜子,
很容易得到正确的英文为.
故答案为:.
14.14
【分析】本题考查了折叠的性质,三角形的内角和定理,根据折叠的性质,得到,进而计算周长即可.
【详解】解:由折叠可知,,
的周长.
故答案为:14.
15.
【分析】本题主要考查了轴对称图形的概念.本题根据轴对称图形的概念即可找出符合题意的小方格,注意不要遗漏.
【详解】解:如图所示,有4个位置使之成为轴对称图形.
故答案为:.
16.
【分析】在上截取,连接,,可证,根据全等三角形的性质可知点和点关于对称,再根据轴对称的性质及最短路径结合面积法即可得出答案.
【详解】解:如图,在上截取,连接,,
是的平分线,
在与中
点和点关于对称,连接,与交于点,连接,
此时,
是动点,
也是动点,当与垂直时,最小,即最小.
此时,由面积法得.
故答案为:.
【点睛】本题考查利用轴对称求最短距离,能够利用轴对称将线段和的最小值转化为线段长求解是关键.
17.
【分析】此题考查轴对称的性质、三角形的周长等知识,熟练掌握轴对称的性质是解题的关键.由折叠得,则,所以,求得.
【详解】由折叠可知:,
周长为8,
∴,
∴,
∵,
,
∴.
18.(1)
(2)四边形是菱形,理由见解析
【分析】本题考点涉及等腰三角形的性质、旋转的性质、三角形外角和定理、平行线的判定、平行四边形的判定、菱形的判定,涉及知识点较多,但难度不大,熟练掌握相关性质定理是解题关键.
(1)利用等腰三角形性质得出,利用旋转的性质和三角形的外角定理即可解答;
(2)利用平行线的判定定理证得,所以四边形是平行四边形,再利用菱形判定定理即可解决问题.
【详解】(1)解:∵
∴,
∵将绕点A顺时针方向旋转得到,
∴,
∴;
(2)四边形是菱形,理由如下:
∵,
∴,
∵
∴
∴四边形是平行四边形,且,
∴四边形是菱形.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.中国“二十四节气”已被列入联合国教科文组织人类非物质文化遗产代表作名录,下列四幅作品分别代 表“大雪”、“白露”、“芒种”、“立春”,其中是轴对称图形的是( )
A. B. C. D.
2.下列图标中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
3.2023年秋季,19届亚运会在杭州如火如荼地进行,运动健儿们摘金夺银,全国人民感受到一波强烈的民族自豪感.下列图案表示的运动项目标志中,是轴对称图形的是( )
A. B. C. D.
4.如图,在正方形网格中,绕某一点旋转某一角度得到,则旋转中心可能是( )
A.点A B.点B C.点C D.点D
5.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
6.下列各曲线是在平面直角坐标系中根据不同的方程绘制而成的,其中是中心对称图形的是( )
A. B. C. D.
7.如图,将绕点C逆时针旋转度后得到,点A,B的对应点分别为点D,E,连接与交于点F,点A,B,E,F在同直一线上,则下列结论一定正确的是( )
A. B.
C. D.
8.做好“垃圾分类”,倡导绿色健康的生活方式,是我们做为公民应尽的义务,如图所示垃圾分类标志,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
9.视力表中的字母“E”有各种不同的摆放方向,下面每种组合中的两个字母“E”不能关于直线l成轴对称的是( )
A. B.
C. D.
10.如图的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )
A. 科克曲线 B. 笛卡尔心形线
C. 赵爽弦图 D. 斐波那契螺旋线
评卷人得分
二、填空题
11.如图,将一张纸条折叠,若,则的度数为 °.
12.如图,桌球的桌面上有,两个球,若要将球射向桌面的一边,反弹一次后击中球,则,,,,4个点中,可以反弹击中球的是 点.
13.王红在电脑中用英文写个人简历时,把其中一句倒排成:则正确的英文为 .
14.如图,在中,将沿直线折叠,使点与点重合,连接.若,,则的周长为 .
15.如图是正方形网格,其中已有3个小方格涂成了黑色,现在要从其余白色小方格中选出一个也涂成黑色,使黑色图形成为轴对称图形,这样的白色小方格有 个.
16.如图,在中,,,,,是的平分线.若点P,Q分别是和上的动点,则的最小值是
评卷人得分
三、问答题
17.如图,在中,,折叠该纸片,使点落在点处,折痕为,若的周长为8,求的长.
18.如图,中,,将绕点A逆时针方向旋转得到,与交于点G、F.
(1)求的度数;
(2)判断四边形的形状,并说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】本题考查了轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合.根据轴对称图形的知识求解.
【详解】解:A、是轴对称图形,故本选项符合题意;
B、不是轴对称图形,故本选项不符合题意;
C、不是轴对称图形,故本选项不符合题意;
D、不是轴对称图形,故本选项不符合题意.
故选:A.
2.C
【分析】中心对称图形定义:把一个图形绕着某个点旋转,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形;轴对称图形定义:如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形,根据定义逐项判断即可得出结论.本题考查中心对称图形与轴对称图形,熟练掌握中心对称图形与轴对称图形的定义是解决问题的关键.
【详解】解:A、不是轴对称图形,是中心对称图形,故选项不符合题意;
B、不是轴对称图形,不是中心对称图形,故选项不符合题意;
C、既是轴对称图形,又是中心对称图形,故选项符合题意;
D、是轴对称图形,不是中心对称图形,故选项不符合题意;
故选:C.
3.B
【分析】本题考查的是轴对称图形的识别.根据一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
【详解】解:A.不是轴对称图形,不符合题意;
B.是轴对称图形,符合题意;
C.不是轴对称图形,不符合题意;
D.不是轴对称图形,不符合题意;
故选:B.
4.B
【分析】如图:连接,作的垂直平分线,作的垂直平分线,两垂直平分线的交点即为旋转中心;掌握旋转中心的确定方法是解题的关键.
【详解】解:如图,
∵绕某点旋转一定的角度,得到,
∴连接,作的垂直平分线,作的垂直平分线,
∴三条线段的垂直平分线正好都过B,即旋转中心是B.
故选:B.
5.B
【分析】本题考查了中心对称图形与轴对称图形,根据轴对称图形和中心对称图形的定义进行逐一判断即可:如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形;把一个图形绕着某一个点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.掌握中心对称图形与轴对称图形的判断是解题的关键.
【详解】解:A、是中心对称图形,但不是轴对称图形,故不符合题意;
B、既是轴对称图形,也是中心对称图形,故符合题意;
C、是轴对称图形,但不是中心对称图形,故不符合题意;
D、不是轴对称图形,也不是中心对称图形,故符合题意.
故选:B.
6.C
【分析】本题主要是考查了中心对称图形的定义,熟练掌握中心对图形的定义“旋转180°能与自身重合的图形即为中心对称图形”,是解决该题的关键.
【详解】解:解:A、不是中心对称图形,故A错误.
B、不是中心对称图形,故B错误.
C、是中心对称图形,故C正确.
D、不是中心对称图形,故D错误.
故选:C.
7.C
【分析】根据旋转的性质和反证法进行证明即可得到答案.熟练掌握反证法是解题的关键.
【详解】解:解:A.∵将绕点C逆时针旋转度后得到,
∴,
但无法确定,故选项错误,不符合题意;
B.∵将绕点C逆时针旋转度后得到,
∴,
∴,,
若,则,
∴,
∴,
∴,
∴是等边三角形,
∴,
∴,
∵大小未知,
故选项错误,不符合题意;
C.∵将绕点C逆时针旋转度后得到,
∴,
∴,
∵,
∴,
∴,
故选项正确,符合题意;
D.∵将绕点C逆时针旋转度后得到,
∴,
若,
∵,
∴,
即是等边三角形,
当且仅当时成立,
故选项错误,不符合题意.
故选:C.
8.C
【分析】本题考查了轴对称图形和中心对称图形的识别,根据轴对称图形的定义:平面内,一个图形沿一条直线折叠 ,直线两旁的部分能够完全重合的图形,中心对称图形的定义:把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,据此逐项判断即可.
【详解】解:A、该图形既不是轴对称图形,也不是中心对称图形,本项不符合题意;
B、该图形是轴对称图形,但不是中心对称图形,本项不符合题意;
C、该图形既是轴对称图形,也是中心对称图形,本项符合题意;
D、该图形不是轴对称图形,也不是中心对称图形,本项不符合题意;
故答案为:C.
9.D
【分析】本题主要考查了轴对称的图形,根据轴对称图形的定义解题即可.
【详解】解:A、两个字母“E”关于直线l成轴对称,故本选项不符合题意;
B、两个字母“E”关于直线l成轴对称,故本选项不符合题意;
C、两个字母“E”关于直线l成轴对称,故本选项不符合题意;
D、两个字母“E”不能沿着直线 l翻折互相重合,故本选项符合题意.
故选:D.
10.A
【分析】本题考查了中心对称图形与轴对称图形,根据轴对称图形和中心对称图形的定义进行逐一判断即可:如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形;把一个图形绕着某一个点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.掌握中心对称图形与轴对称图形的判断是解题的关键.
【详解】解:A、既是轴对称图形,也是中心对称图形,故符合题意;
B、是轴对称图形,但不是中心对称图形,故不符合题意;
C、不是轴对称图形,是中心对称图形,故不符合题意;
D、既不是轴对称图形,也不是中心对称图形,故符合题意;
故选:A.
11.
【分析】根据折叠的性质即可得出关于的一元一次方程,解之即可得出结论.本题考查角的计算以及折叠的性质,解题的关键是明确题意,掌握折叠前后的对应角相等的性质.
【详解】解: 根据折叠的性质可知:,
即,
解得:.
故答案为:.
12.D
【分析】本题考查了轴对称的性质,解题关键是根据轴对称的性质找到使入射角等于反射角相等的点.
【详解】解:如图,根据轴对称的性质可知,可以反弹击中球的是D点,
故选:D.
13.
【分析】本题是镜面反射的知识,可以在这句话的正上方放一面镜子,看镜子里的字母就可以了.
【详解】解:如图在这句话的正上方放一面镜子,
很容易得到正确的英文为.
故答案为:.
14.14
【分析】本题考查了折叠的性质,三角形的内角和定理,根据折叠的性质,得到,进而计算周长即可.
【详解】解:由折叠可知,,
的周长.
故答案为:14.
15.
【分析】本题主要考查了轴对称图形的概念.本题根据轴对称图形的概念即可找出符合题意的小方格,注意不要遗漏.
【详解】解:如图所示,有4个位置使之成为轴对称图形.
故答案为:.
16.
【分析】在上截取,连接,,可证,根据全等三角形的性质可知点和点关于对称,再根据轴对称的性质及最短路径结合面积法即可得出答案.
【详解】解:如图,在上截取,连接,,
是的平分线,
在与中
点和点关于对称,连接,与交于点,连接,
此时,
是动点,
也是动点,当与垂直时,最小,即最小.
此时,由面积法得.
故答案为:.
【点睛】本题考查利用轴对称求最短距离,能够利用轴对称将线段和的最小值转化为线段长求解是关键.
17.
【分析】此题考查轴对称的性质、三角形的周长等知识,熟练掌握轴对称的性质是解题的关键.由折叠得,则,所以,求得.
【详解】由折叠可知:,
周长为8,
∴,
∴,
∵,
,
∴.
18.(1)
(2)四边形是菱形,理由见解析
【分析】本题考点涉及等腰三角形的性质、旋转的性质、三角形外角和定理、平行线的判定、平行四边形的判定、菱形的判定,涉及知识点较多,但难度不大,熟练掌握相关性质定理是解题关键.
(1)利用等腰三角形性质得出,利用旋转的性质和三角形的外角定理即可解答;
(2)利用平行线的判定定理证得,所以四边形是平行四边形,再利用菱形判定定理即可解决问题.
【详解】(1)解:∵
∴,
∵将绕点A顺时针方向旋转得到,
∴,
∴;
(2)四边形是菱形,理由如下:
∵,
∴,
∵
∴
∴四边形是平行四边形,且,
∴四边形是菱形.
答案第1页,共2页
答案第1页,共2页
