第一章 直角三角形的边角关系第一节锐角三角函数(共40张PPT)
文档属性
| 名称 | 第一章 直角三角形的边角关系第一节锐角三角函数(共40张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 08:56:25 | ||
图片预览






文档简介
(共40张PPT)
第一章 直角三角形的边角关系
第一节锐角三角函数
北师大版九年级上册
教学目标
通过比较现实情境中梯子的陡与缓,会用不同方法刻画梯子的倾斜程度,发展几何直观与抽象能力.
能结合图形说明正切、正弦、余弦的含义,能准确用 tanA,sinA,cosA 表示直角三角形中两边的比,在已知边长的直角三角形中,会求一个锐角的正切、正弦、余弦,发展抽象能力与运算能力.
能运用直角三角形边角关系解决简单的问题,提升应用能力.
复习回顾
几何图形是数学研究的主要对象之一。研究任何一种几何图形,都是按照定义-性质-判定的思路展开的,其中的性质就是要研究组成图形的各个元素的特征以及元素之间的关系。
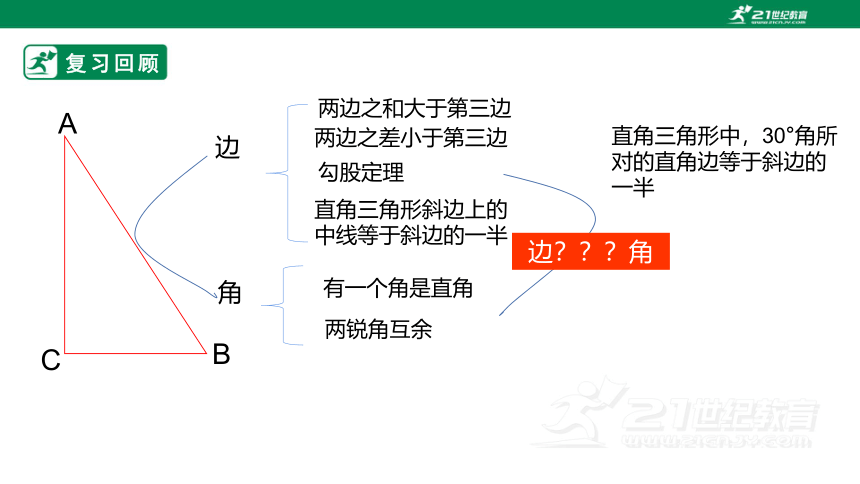
复习回顾
边
勾股定理
直角三角形斜边上的中线等于斜边的一半
两边之差小于第三边
角
有一个角是直角
两锐角互余
直角三角形中,30°角所对的直角边等于斜边的一半
两边之和大于第三边
A
B
C
边???角
探究感悟
活动一:比较梯子的倾斜程度
探究感悟
40°
A
B
C
55°
D
E
F
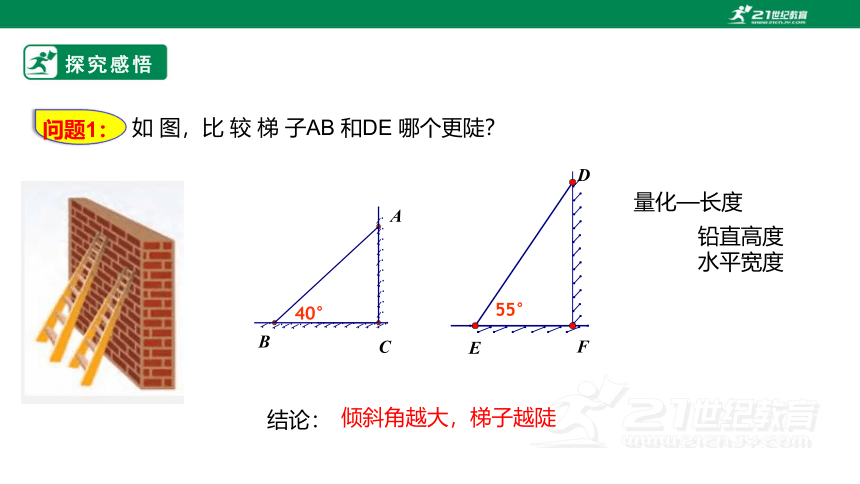
如 图,比 较 梯 子AB 和DE 哪个更陡?
结论:
倾斜角越大,梯子越陡
量化—长度
铅直高度
水平宽度
问题1:
探究感悟
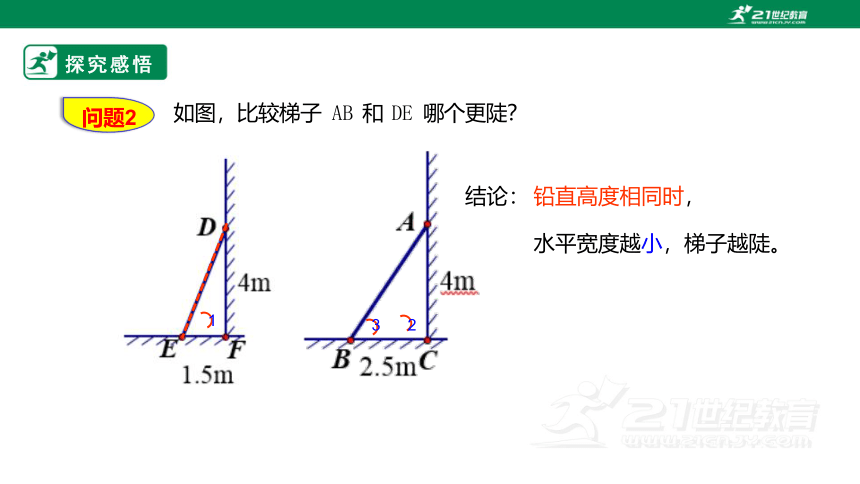
如图,比较梯子 AB 和 DE 哪个更陡?
铅直高度相同时,
水平宽度越小,梯子越陡。
结论:
⌒
⌒
⌒
1
2
3
问题2
探究感悟
如图,比较梯子 AB 和 DE 哪个更陡?
1
⌒
⌒
⌒
3
2
水平宽度相同时,铅直高度越大,梯子越陡。
结论:
问题3
探究感悟
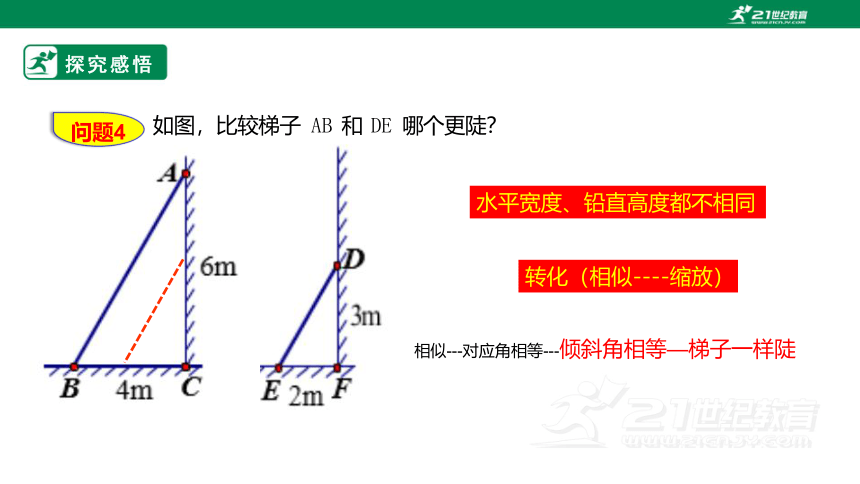
如图,比较梯子 AB 和 DE 哪个更陡?
水平宽度、铅直高度都不相同
相似---对应角相等---倾斜角相等—梯子一样陡
转化(相似----缩放)
问题4
探究感悟
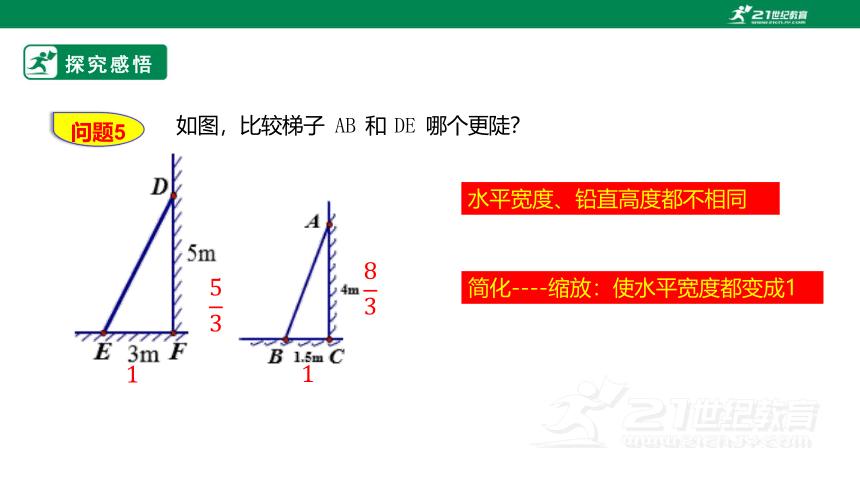
如图,比较梯子 AB 和 DE 哪个更陡?
水平宽度、铅直高度都不相同
简化----缩放:使水平宽度都变成1
问题5
探究感悟
简化----缩放:使水平宽度a都变成1
刻
画
倾斜程度
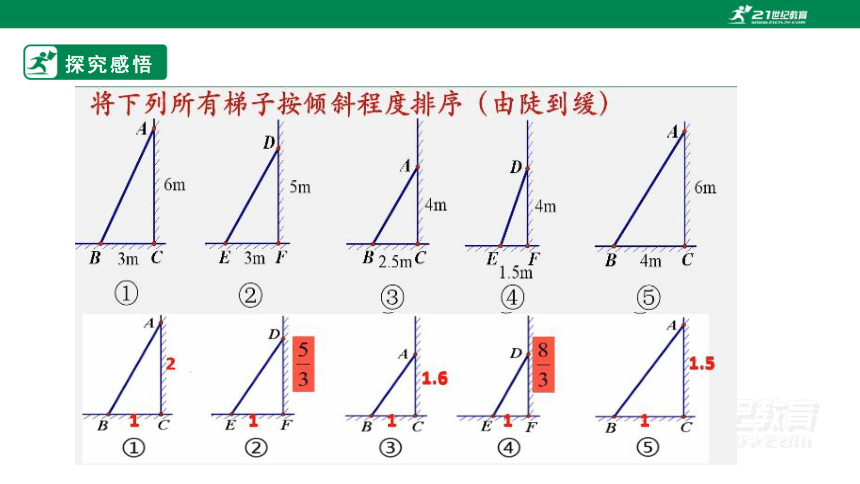
一般化图形---比较梯子的倾斜程度
探究感悟
通过一组探究后,思考梯子的倾斜程度与什么相关?
刻
画
倾斜程度
倾斜角
刻
画
倾斜程度
问题6
探究感悟
探究活动二:探索角度与比值的关系
= =
计算∠A的对边与邻边的比值
A
B
C
⌒
30°
∠A=30°
1
= =1
∠A=45°
…...
…...
比值
角度
对应关系
大量例子说明
?
探究感悟
N
A
B
C
B1
C1
B2
B3
C2
C3
M
=
=
=
推理论证
探究感悟
在直角三角形中,当一个锐角的度数变化时,它的对边与邻边的比值也随之变化,而对于锐角的每一个确定的度数,对边与邻边的比值都是唯一确定的。这种角度和比值之间存在一种对应关系
函数关系
正切三角函数
在直角三角形中,锐角与这个比值究竟是一种什么关系?
对边与邻边的比值
探究感悟
活动三:建立概念 锐角三角函数
A
B
C
⌒
∠A的对边
∠A的邻边
∠A的对边
∠A的邻边
tan∠A=
∠A的正切
几何语言:
在Rt 中, ∠C=90°
=
定义:在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切(tangent),记作tanA,
探究感悟
定义的几点说明:
1)初中阶段,正切是在直角三角形中定义的, ∠A是一个锐角.
2) tanA是一个完整的符号,它表示∠A的正切,记号里习惯省去角的符号“∠”。但∠BAC的正切表示为:tan∠BAC,∠1的正切表示为:tan∠1.
3) tanA没有单位,它表示一个比值,即直角三角形中锐角∠A的对边与邻边的比(注意顺序: ).
4) tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
探究感悟
活动三:建立概念 ----锐角三角函数
在Rt 中, ∠C=90°,
A
B
C
⌒
∠B的邻边
∠B的对边
∠B的正切值
∠B的对边
∠B的邻边
几何语言:
在Rt 中, ∠C=90°
=
探究感悟
活动三:建立概念 ---锐角三角函数
∠A的对边
在Rt 中, ∠C=90°
A
B
C
斜边
思考:当Rt△ABC中锐角A确定时,∠A的对边与∠A的邻边之比是一个定值,那∠A的对边与斜边之比呢
∠A的正弦
∠A的对边
斜边
SinA=
几何语言:
在Rt 中, ∠C=90°
角度:倾斜角
-- 梯子与地面的夹角
⌒
倾斜角
水平宽度a
铅直高度b
探究感悟
活动三:建立概念 ---锐角三角函数
∠A的邻边
在Rt 中, ∠C=90°
A
B
C
斜边
再思考:Rt△ABC中,∠A的邻边与斜边之比呢
∠A的余弦
∠A的邻边
斜边
CosA=
几何语言:
在Rt 中, ∠C=90°
探究感悟
锐角A的正弦,余弦和正切都是∠A的三角函数 (trigonometric function) 。
当锐角A变化时,相应的正弦,余弦和正切值也随之变化。因此,正弦和余弦也同样能刻画梯子的倾斜程度。
∠A的对边
∠A的邻边
tanA=
∠A的正切
∠A的正弦
∠A的对边
斜边
SinA=
∠A的余弦
∠A的邻边
斜边
CosA=
活动三:建立概念 ---锐角三角函数
探究感悟
在Rt 中, ∠C=90°
斜边
∠B的对边
∠B的邻边
tanB=
∠B的正切
∠B的正弦
∠B的对边
斜边
SinB=
∠B的余弦
∠B的邻边
斜边
CosB=
∠B的邻边
∠B的对边
A
B
C
⌒
活动三:建立概念 ---锐角三角函数
探究感悟
例1.如图,在Rt△ABC中,∠B=90°,若AB =5,BC=12,则sinA =____; tanC=___; cosC=____
活动四:理解概念—锐角三角函数
探究感悟
活动四:理解概念
探究感悟
活动四:理解概念
探究感悟
例4.下图表示甲、乙两个自动扶梯,哪一个自动扶梯比较陡
活动四:理解概念
探究感悟
活动五:总结概念 锐角三角函数
探究感悟
活动六:概念延伸—坡度(坡比)
如图,正切也经常用来描述山坡的坡度.例如,有一山坡在水平方向上每前进100m就升高60m,那么山坡的坡度i(即tanα)就是:
1.坡面与水平面的夹角(α)叫坡角。
2.坡面的铅直高度与水平宽度的比称为坡度i(或坡比),即坡度等于坡角的正切。
3.坡度越大,坡面越陡。
课堂总结
达标自测
1.如图,在 Rt△ACB 中,∠B=90°,若 AB=7,BC=24, 则 sinA= ;tanC= ;cosC= .
达标自测
2.如图,在 Rt△ABC 中,∠C=90°,BC=10,,则 AC= .
达标自测
3.在 Rt△ABC 中,各边的长度同时扩大为原来的 2 倍,cosA 的值( )
达标自测
4.如图,某人从山脚下的点 A 处走了 1000 米爬到了山顶的点 B 处,已知点 B 到山脚的垂直距离为 600 米,则该山坡的坡度为 .
达标自测
5.在等腰△ABC 中,若 AB=AC=5,BC=6,则 sinB= ,cosB= ,tanB=
达标自测
6.在 Rt△ABC 中,∠B=90°,sinA 与 cosC 有什么关系?
作业布置
教材习题1.1
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第一章 直角三角形的边角关系
第一节锐角三角函数
北师大版九年级上册
教学目标
通过比较现实情境中梯子的陡与缓,会用不同方法刻画梯子的倾斜程度,发展几何直观与抽象能力.
能结合图形说明正切、正弦、余弦的含义,能准确用 tanA,sinA,cosA 表示直角三角形中两边的比,在已知边长的直角三角形中,会求一个锐角的正切、正弦、余弦,发展抽象能力与运算能力.
能运用直角三角形边角关系解决简单的问题,提升应用能力.
复习回顾
几何图形是数学研究的主要对象之一。研究任何一种几何图形,都是按照定义-性质-判定的思路展开的,其中的性质就是要研究组成图形的各个元素的特征以及元素之间的关系。
复习回顾
边
勾股定理
直角三角形斜边上的中线等于斜边的一半
两边之差小于第三边
角
有一个角是直角
两锐角互余
直角三角形中,30°角所对的直角边等于斜边的一半
两边之和大于第三边
A
B
C
边???角
探究感悟
活动一:比较梯子的倾斜程度
探究感悟
40°
A
B
C
55°
D
E
F
如 图,比 较 梯 子AB 和DE 哪个更陡?
结论:
倾斜角越大,梯子越陡
量化—长度
铅直高度
水平宽度
问题1:
探究感悟
如图,比较梯子 AB 和 DE 哪个更陡?
铅直高度相同时,
水平宽度越小,梯子越陡。
结论:
⌒
⌒
⌒
1
2
3
问题2
探究感悟
如图,比较梯子 AB 和 DE 哪个更陡?
1
⌒
⌒
⌒
3
2
水平宽度相同时,铅直高度越大,梯子越陡。
结论:
问题3
探究感悟
如图,比较梯子 AB 和 DE 哪个更陡?
水平宽度、铅直高度都不相同
相似---对应角相等---倾斜角相等—梯子一样陡
转化(相似----缩放)
问题4
探究感悟
如图,比较梯子 AB 和 DE 哪个更陡?
水平宽度、铅直高度都不相同
简化----缩放:使水平宽度都变成1
问题5
探究感悟
简化----缩放:使水平宽度a都变成1
刻
画
倾斜程度
一般化图形---比较梯子的倾斜程度
探究感悟
通过一组探究后,思考梯子的倾斜程度与什么相关?
刻
画
倾斜程度
倾斜角
刻
画
倾斜程度
问题6
探究感悟
探究活动二:探索角度与比值的关系
= =
计算∠A的对边与邻边的比值
A
B
C
⌒
30°
∠A=30°
1
= =1
∠A=45°
…...
…...
比值
角度
对应关系
大量例子说明
?
探究感悟
N
A
B
C
B1
C1
B2
B3
C2
C3
M
=
=
=
推理论证
探究感悟
在直角三角形中,当一个锐角的度数变化时,它的对边与邻边的比值也随之变化,而对于锐角的每一个确定的度数,对边与邻边的比值都是唯一确定的。这种角度和比值之间存在一种对应关系
函数关系
正切三角函数
在直角三角形中,锐角与这个比值究竟是一种什么关系?
对边与邻边的比值
探究感悟
活动三:建立概念 锐角三角函数
A
B
C
⌒
∠A的对边
∠A的邻边
∠A的对边
∠A的邻边
tan∠A=
∠A的正切
几何语言:
在Rt 中, ∠C=90°
=
定义:在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切(tangent),记作tanA,
探究感悟
定义的几点说明:
1)初中阶段,正切是在直角三角形中定义的, ∠A是一个锐角.
2) tanA是一个完整的符号,它表示∠A的正切,记号里习惯省去角的符号“∠”。但∠BAC的正切表示为:tan∠BAC,∠1的正切表示为:tan∠1.
3) tanA没有单位,它表示一个比值,即直角三角形中锐角∠A的对边与邻边的比(注意顺序: ).
4) tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
探究感悟
活动三:建立概念 ----锐角三角函数
在Rt 中, ∠C=90°,
A
B
C
⌒
∠B的邻边
∠B的对边
∠B的正切值
∠B的对边
∠B的邻边
几何语言:
在Rt 中, ∠C=90°
=
探究感悟
活动三:建立概念 ---锐角三角函数
∠A的对边
在Rt 中, ∠C=90°
A
B
C
斜边
思考:当Rt△ABC中锐角A确定时,∠A的对边与∠A的邻边之比是一个定值,那∠A的对边与斜边之比呢
∠A的正弦
∠A的对边
斜边
SinA=
几何语言:
在Rt 中, ∠C=90°
角度:倾斜角
-- 梯子与地面的夹角
⌒
倾斜角
水平宽度a
铅直高度b
探究感悟
活动三:建立概念 ---锐角三角函数
∠A的邻边
在Rt 中, ∠C=90°
A
B
C
斜边
再思考:Rt△ABC中,∠A的邻边与斜边之比呢
∠A的余弦
∠A的邻边
斜边
CosA=
几何语言:
在Rt 中, ∠C=90°
探究感悟
锐角A的正弦,余弦和正切都是∠A的三角函数 (trigonometric function) 。
当锐角A变化时,相应的正弦,余弦和正切值也随之变化。因此,正弦和余弦也同样能刻画梯子的倾斜程度。
∠A的对边
∠A的邻边
tanA=
∠A的正切
∠A的正弦
∠A的对边
斜边
SinA=
∠A的余弦
∠A的邻边
斜边
CosA=
活动三:建立概念 ---锐角三角函数
探究感悟
在Rt 中, ∠C=90°
斜边
∠B的对边
∠B的邻边
tanB=
∠B的正切
∠B的正弦
∠B的对边
斜边
SinB=
∠B的余弦
∠B的邻边
斜边
CosB=
∠B的邻边
∠B的对边
A
B
C
⌒
活动三:建立概念 ---锐角三角函数
探究感悟
例1.如图,在Rt△ABC中,∠B=90°,若AB =5,BC=12,则sinA =____; tanC=___; cosC=____
活动四:理解概念—锐角三角函数
探究感悟
活动四:理解概念
探究感悟
活动四:理解概念
探究感悟
例4.下图表示甲、乙两个自动扶梯,哪一个自动扶梯比较陡
活动四:理解概念
探究感悟
活动五:总结概念 锐角三角函数
探究感悟
活动六:概念延伸—坡度(坡比)
如图,正切也经常用来描述山坡的坡度.例如,有一山坡在水平方向上每前进100m就升高60m,那么山坡的坡度i(即tanα)就是:
1.坡面与水平面的夹角(α)叫坡角。
2.坡面的铅直高度与水平宽度的比称为坡度i(或坡比),即坡度等于坡角的正切。
3.坡度越大,坡面越陡。
课堂总结
达标自测
1.如图,在 Rt△ACB 中,∠B=90°,若 AB=7,BC=24, 则 sinA= ;tanC= ;cosC= .
达标自测
2.如图,在 Rt△ABC 中,∠C=90°,BC=10,,则 AC= .
达标自测
3.在 Rt△ABC 中,各边的长度同时扩大为原来的 2 倍,cosA 的值( )
达标自测
4.如图,某人从山脚下的点 A 处走了 1000 米爬到了山顶的点 B 处,已知点 B 到山脚的垂直距离为 600 米,则该山坡的坡度为 .
达标自测
5.在等腰△ABC 中,若 AB=AC=5,BC=6,则 sinB= ,cosB= ,tanB=
达标自测
6.在 Rt△ABC 中,∠B=90°,sinA 与 cosC 有什么关系?
作业布置
教材习题1.1
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
