27.1 图形的相似(第2课时) 课件(共20张PPT)
文档属性
| 名称 | 27.1 图形的相似(第2课时) 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1017.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
图形的相似(第2课时)
什么是相似图形?
我们把形状相同的图形叫做相似图形.
什么情况下四条线段成比例?
对于四条线段 a,b,c,d,如果其中两条线段的比与另两条线段的比相等,如 (即 ad=bc),我们就说这四条线段成比例.
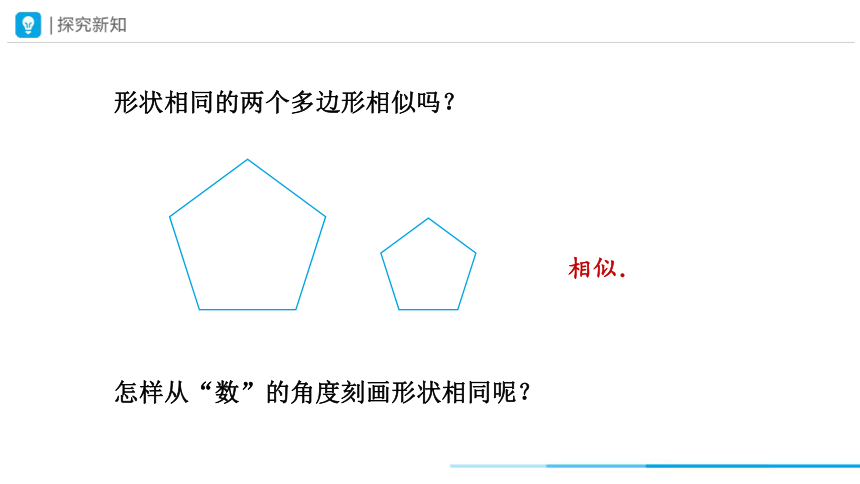
形状相同的两个多边形相似吗?
相似.
怎样从“数”的角度刻画形状相同呢?
A
C
B
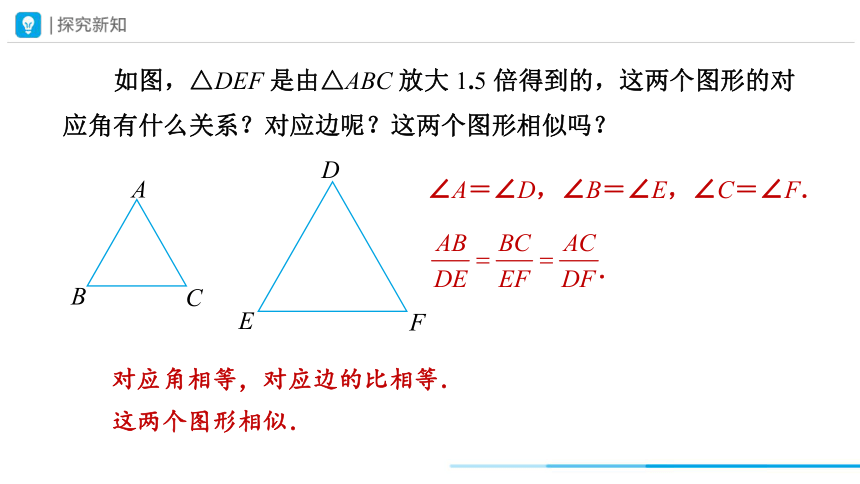
如图,△DEF 是由△ABC 放大 1.5 倍得到的,这两个图形的对应角有什么关系?对应边呢?这两个图形相似吗?
D
F
E
∠A=∠D,∠B=∠E,∠C=∠F.
.
对应角相等,对应边的比相等.
这两个图形相似.
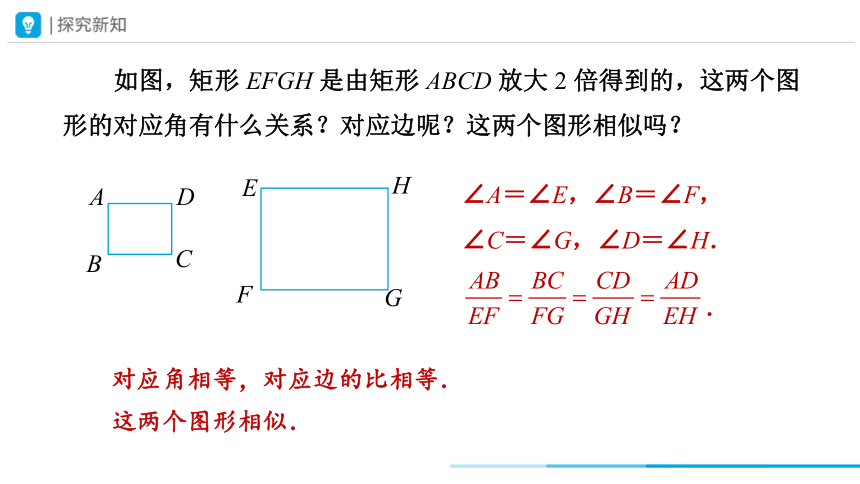
如图,矩形 EFGH 是由矩形 ABCD 放大 2 倍得到的,这两个图形的对应角有什么关系?对应边呢?这两个图形相似吗?
A
B
C
D
G
E
H
F
∠A=∠E,∠B=∠F,
∠C=∠G,∠D=∠H.
.
对应角相等,对应边的比相等.
这两个图形相似.
两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.相似多边形对应边的比叫做相似比.
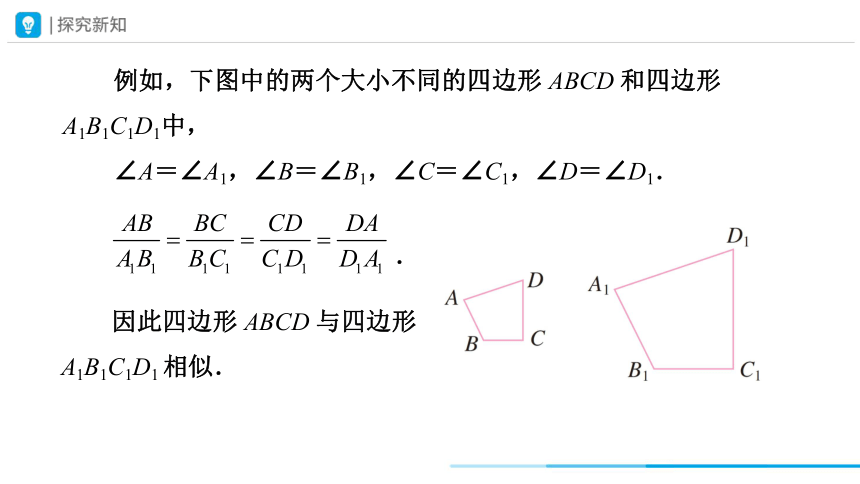
例如,下图中的两个大小不同的四边形 ABCD 和四边形 A1B1C1D1中,
∠A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1.
.
因此四边形 ABCD 与四边形 A1B1C1D1 相似.
注意:
两个多边形相似,必须同时具备三个条件:
(1)边数相同;
(2)角分别相等;
(3)边成比例.
△DEF 是由△ABC 放大 1.5 倍得到的,则△DEF 与△ABC 的相似比是多少?
1.5
相似比的实质是把一个图形放大或缩小的倍数.
注意:
相似比的值与两个多边形的顺序有关.例如:若四边形 EFGH 与四边形 ABCD 的相似比为 2,则四边形 ABCD 与四边形 EFGH 的相似比为 .
全等的两个图形的相似比为 1.
任意两个等边三角形相似吗?任意两个正方形呢?任意两个正 n 边形呢?
a1
a2
a3
an
…
等边三角形的每个角都为 60°,三边都相等.所以满足边数相同,对应角相等,对应边的比相等.故任意两个等边三角形相似.
任意两个等边三角形相似吗?任意两个正方形呢?任意两个正 n 边形呢?
a1
a2
a3
an
正方形的每个角都为 90°,四边都相等.所以满足边数相同,对应角相等,对应边的比相等.故任意两个正方形相似.
任意两个边数相等的正多边形都相似.
…
任意两个菱形(或矩形)是否相似?为什么?
角不相等
边不成比例
不相似
如果两个多边形相似,那么它们的角有什么关系?它们的边呢?
相似多边形的性质:相似多边形的对应角相等,对应边成比例.
例1 如图,四边形 ABCD 和 EFGH 相似,求角 α,β 的大小和 EH 的长度 x.
解:因为四边形 ABCD 和 EFGH 相似,所以它们的对应角相等,
由此可得 α=∠C=83°,∠A=∠E=118°.
在四边形 ABCD 中,β=360°-(78°+83°+118°)=81°.
因为四边形 ABCD 和 EFGH 相似,所以它们的对应边成比例.
由此可得 ,即 .
解得 x=28.
相似多边形的性质常用来求相似多边形未知边的长度或未知角的度数.
例2 如图,DE∥BC.
(1)求 , , 的值;
(2)证明 △ADE 与△ABC 相似.
(1)解: , , .
(2)证明:由(1)知
.
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
又∵∠A=∠A,
∴△ADE 与△ABC 相似.
相似多边形的定义可用来判定两个多边形是否相似.
依据:定义
相似多边形
性质
概念
对应角相等
对应边成比例
相似比
图形的相似(第2课时)
什么是相似图形?
我们把形状相同的图形叫做相似图形.
什么情况下四条线段成比例?
对于四条线段 a,b,c,d,如果其中两条线段的比与另两条线段的比相等,如 (即 ad=bc),我们就说这四条线段成比例.
形状相同的两个多边形相似吗?
相似.
怎样从“数”的角度刻画形状相同呢?
A
C
B
如图,△DEF 是由△ABC 放大 1.5 倍得到的,这两个图形的对应角有什么关系?对应边呢?这两个图形相似吗?
D
F
E
∠A=∠D,∠B=∠E,∠C=∠F.
.
对应角相等,对应边的比相等.
这两个图形相似.
如图,矩形 EFGH 是由矩形 ABCD 放大 2 倍得到的,这两个图形的对应角有什么关系?对应边呢?这两个图形相似吗?
A
B
C
D
G
E
H
F
∠A=∠E,∠B=∠F,
∠C=∠G,∠D=∠H.
.
对应角相等,对应边的比相等.
这两个图形相似.
两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.相似多边形对应边的比叫做相似比.
例如,下图中的两个大小不同的四边形 ABCD 和四边形 A1B1C1D1中,
∠A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1.
.
因此四边形 ABCD 与四边形 A1B1C1D1 相似.
注意:
两个多边形相似,必须同时具备三个条件:
(1)边数相同;
(2)角分别相等;
(3)边成比例.
△DEF 是由△ABC 放大 1.5 倍得到的,则△DEF 与△ABC 的相似比是多少?
1.5
相似比的实质是把一个图形放大或缩小的倍数.
注意:
相似比的值与两个多边形的顺序有关.例如:若四边形 EFGH 与四边形 ABCD 的相似比为 2,则四边形 ABCD 与四边形 EFGH 的相似比为 .
全等的两个图形的相似比为 1.
任意两个等边三角形相似吗?任意两个正方形呢?任意两个正 n 边形呢?
a1
a2
a3
an
…
等边三角形的每个角都为 60°,三边都相等.所以满足边数相同,对应角相等,对应边的比相等.故任意两个等边三角形相似.
任意两个等边三角形相似吗?任意两个正方形呢?任意两个正 n 边形呢?
a1
a2
a3
an
正方形的每个角都为 90°,四边都相等.所以满足边数相同,对应角相等,对应边的比相等.故任意两个正方形相似.
任意两个边数相等的正多边形都相似.
…
任意两个菱形(或矩形)是否相似?为什么?
角不相等
边不成比例
不相似
如果两个多边形相似,那么它们的角有什么关系?它们的边呢?
相似多边形的性质:相似多边形的对应角相等,对应边成比例.
例1 如图,四边形 ABCD 和 EFGH 相似,求角 α,β 的大小和 EH 的长度 x.
解:因为四边形 ABCD 和 EFGH 相似,所以它们的对应角相等,
由此可得 α=∠C=83°,∠A=∠E=118°.
在四边形 ABCD 中,β=360°-(78°+83°+118°)=81°.
因为四边形 ABCD 和 EFGH 相似,所以它们的对应边成比例.
由此可得 ,即 .
解得 x=28.
相似多边形的性质常用来求相似多边形未知边的长度或未知角的度数.
例2 如图,DE∥BC.
(1)求 , , 的值;
(2)证明 △ADE 与△ABC 相似.
(1)解: , , .
(2)证明:由(1)知
.
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
又∵∠A=∠A,
∴△ADE 与△ABC 相似.
相似多边形的定义可用来判定两个多边形是否相似.
依据:定义
相似多边形
性质
概念
对应角相等
对应边成比例
相似比
