14.3.2.2运用完全平方公式因式分解(同步课件)-2023-2024学年八年级数学上册同步精品课堂(人教版)
文档属性
| 名称 | 14.3.2.2运用完全平方公式因式分解(同步课件)-2023-2024学年八年级数学上册同步精品课堂(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 40.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 00:00:00 | ||
图片预览




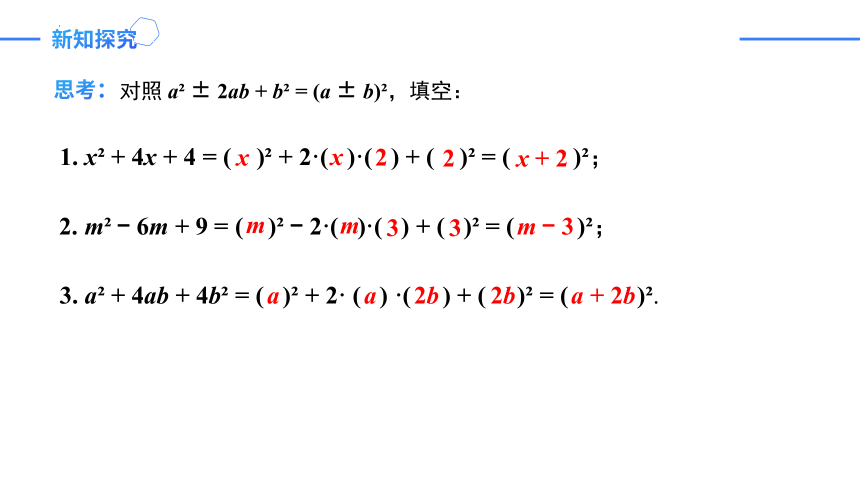


文档简介
第14章
整式的乘法
与因式分解
八年级数学上册同步精品课堂(人教版)
人教版 数学
八年级 上册
14.3.2.2
运用完全平方
公式因式分解
复习回顾
(a+b)2=a2+2ab+b2,
我们把
(a-b)2=a2-2ab+b2.
都叫做完全平方公式.
文字语言:两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的 2 倍. 这两个公式叫做(乘法的)完全平方公式.
符号语言:
“首平方,尾平方,
积的 2 倍放中央.”
复习回顾
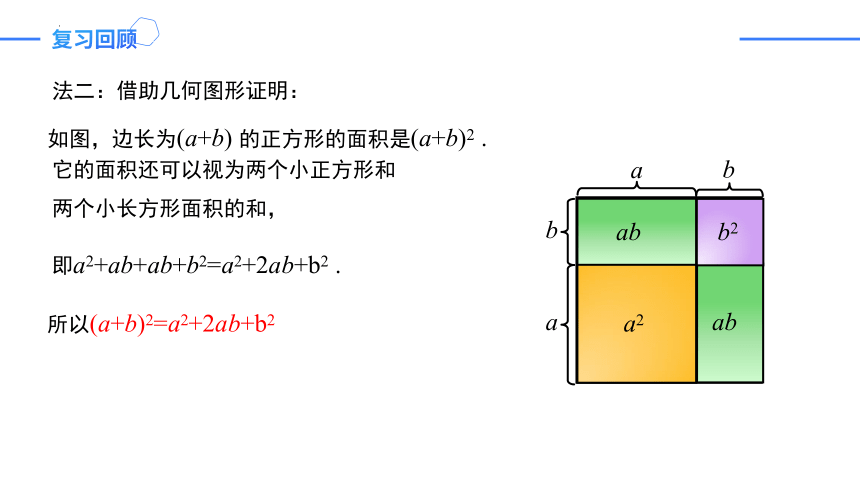
法二:借助几何图形证明:
如图,边长为(a+b) 的正方形的面积是(a+b)2 .
它的面积还可以视为两个小正方形和两个小长方形面积的和,
所以(a+b)2=a2+2ab+b2
b
a
a
b
a2
ab
ab
b2
即a2+ab+ab+b2=a2+2ab+b2 .
复习回顾
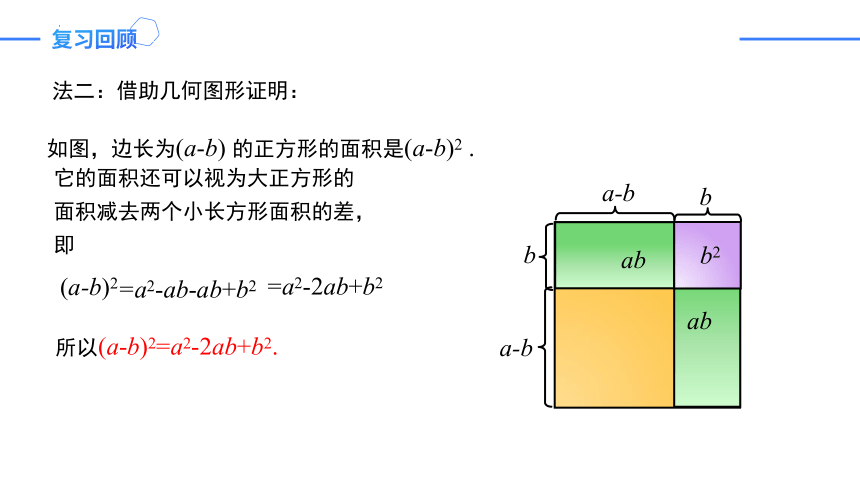
法二:借助几何图形证明:
它的面积还可以视为大正方形的面积减去两个小长方形面积的差,即
如图,边长为(a-b) 的正方形的面积是(a-b)2 .
所以(a-b)2=a2-2ab+b2.
(a-b)2
(a-b2)
a-b
b
b
a-b
ab
ab
b2
=a2-ab-ab+b2
=a2-2ab+b2
复习回顾
思考:
观察下面两个完全平方式,比一比,回答下列问题:
1. 说一说积的次数和项数;
2. 两个完全平方式的积有相同的项吗?与 a,b 有什么关系?
3. 两个完全平方式的积中不同的是哪一项?与 a,b 有什么关系?它的符号与什么有关?
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2.
公式中的字母 a,b 可以表示数,单项式和多项式.
积为二次三项式;
积中两项为两数的平方和;
另一项是两数积的 2 倍,且与两数中间的符号相同;
新知探究
思考:
对照 a? ± 2ab + b? = (a ± b)?,填空:
3. a? + 4ab + 4b? = ( )? + 2· ( ) ·( ) + ( )? = ( )?.
2. m? - 6m + 9 = ( )? - 2·( )·( ) + ( )? = ( )?;
1. x? + 4x + 4 = ( )? + 2·( )·( ) + ( )? = ( )?;
x
2
x + 2
a
a 2b
a + 2b
2b
m
m - 3
3
x
2
m
3
新知探究
思考:
下列各式是不是完全平方式?
(1)a2 - 4a + 4;
(2)1 + 4a?;
(3)4b2 + 4b - 1;
(4)a2 + ab + b2;
(5)x2 + x + 0.25.
是
(2)因为它只有两项.
不是
(3)4b? 与 -1 的符号不统一.
不是
不是
是
(4)因为 ab 不是 a 与 b 的积的 2 倍.
典例精析
例1
已知4????2+????????+36是完全平方式,则 m 的值为(??? ?)
A.8 B.±8 C.24 D.±24
?
【分析】解:∵4????2+????????+36是一个完全平方式,
∴mx=±2?2x?6,
解得:m=±24,
故选:D.
?
D
变式
若 x2 - 6x + N 是一个完全平方式,则 N = ( )
A . 11 B. 9 C. - 11 D. - 9
B
解析:根据完全平方式的特征,中间项 -6x = -2×x×3,故可知 N = 32 = 9.
典例精析
例2
(1)
4x2-4x+1
解:原式=
(2)
分解因式:
解:原式=
(3) -3a2x2 + 24a2x - 48a2;
=(a2 + 4 + 4a)(a2 + 4 - 4a)
解:(3) 原式=-3a2(x2 - 8x + 16)
=-3a2(x - 4)2.
(4) 原式=(a2 + 4)2 - (4a)2
=(a + 2)2(a - 2)2.
(4) (a2 + 4)2 - 16a2.
典例精析
例3
分解因式:
(1) ax2+2a2x+a3 (2) -3x2+6xy-3y2 (3) (x+y)2-12x-12y+36
解:(1)原式= a(x2+2ax+a2)=a(x+a)2
(3)原式=(x+y)2-12(x+y)+36
=(x+y)2-2·(x+y)·6+62
=(a+b-6)2
(2)原式= -3(x2-2xy+y2)=-3(x-y)2
典例精析
例4
(1) (x2+y2)2-4x2y2 (2)4x2(x-1)-16(1-x)2 (3)16x4-72x2+81
解: (1) 原式=(x2+y2+2xy)(x2+y2-2xy)=(x+y)2(x-y)2
(2)原式=4x2(x-1)-16(x-1)2=4(x-1)[x2-4(x-1)]
=4(x-1)(x2-4x+4)=4(x-1)(x-2)2
(3)原式=(4x2)2-2 · 4x2 · 9+92
= (4x2-9)2=[(2x+3)(2x-3)]2
=(2x+3)2(2x-3)2
分解因式:
典例精析
01
02
运用完全平方公式分解因式时,避免与平方差公式混淆.
03
运用完全平方公式分解因式时,有公因式应先提公因式.
运用完全平方公式分解因式时,应注意熟练把握公式的结构特征,避免出现符号、项数上的错误.
典例精析
例5
计算:
(1)3.142+6.28×6.86+6.862;(2)20222?2022×4042+20212.
?
解:(1)3.142+6.28×6.86+6.862
=3.142+2×3.14×6.86+6.862
=3.14+6.862
=102
=100.
?
(2)20222-2022×4042+20212
=20222-2×2022×2021+20212
=(2022-2021)2
=12
=1.
典例精析
例6
(1)已知a-b=3,求a(a-2b)+b2的值;
(2)已知ab=2,a+b=5,求a3b+2a2b2+ab3的值.
解:(1)原式=a2-2ab+b2=(a-b)2.
当a-b=3时,原式=32=9.
(2)原式=ab(a2+2ab+b2)=ab(a+b)2.
当ab=2,a+b=5时,
原式=2×52=50.
典例精析
例7
已知 a,b,c 分别是△ABC 三边的长,且 a2+2b2+c2-2b(a+c) = 0,请判断△ABC 的形状,并说明理由.
∴△ABC 是等边三角形.
解:由 a2+2b2+c2-2b(a+c) = 0,得
a2-2ab+b2+b2-2bc+c2 = 0,
即 (a-b)2+(b-c)2 = 0.
∴ a-b = 0,b-c = 0. ∴ a = b = c.
归纳总结
完全平方公式分解因式
公式
a2±2ab + b2 = (a±b)2
特点
(1)要求多项式有三项;
(2)其中两项是两个数或式的平方和,另一项则是这两数或式的乘积的 2 倍,符号可正可负
当堂检测
1.下列式子为完全平方式的是( )
A. a2+2a+b2 B. a2+2a+2 C. a2-2+b2 D. a2+2a+1.
2.分解因式x2-2x+1的最终结果是( )
A.x(x-2)+1 B. (x+1) (x-2) C. (x-1)2 D. (x+1)2
3.分解因式后结果是-(x-y)2的多项式是( )
A.-x2+2xy-y2 B. x2-2xy-y2 C. x2-2xy+y2 D. -x2-2xy-y2
D
C
A
4.下列分解因式错误的是( )
A. x2-y2= (x+y) (x-y) B. x2+6x+9= (x+3)2
C. x2+xy=x (x+y) D. x2+y2= (x+y)2
D
当堂检测
5.若x2- 2(k+1)x+4是完全平方式,则k的值为( )
A.1或-3 B. -1或3 C.±1 D.±3
6.已知????=????+2,则代数式3????2?6????????+3????2+2022的值为(???? )
A.2020 B.2024 C.2021 D.2034
?
A
D
7.分解因式????2+4????????+4????2?1=__________________________.
8.若x2﹣8x+m2=(x﹣4)2,那么m=_____.
9.若????2+(3?????)????+9可以用完全平方式来分解因式,则m的值为__________.
?
?????或9
?
????+????????+????)(????+?????????????
?
±????
?
当堂检测
10.分解因式:
(1) x2+12x+36 (2) -2xy-x2-y2 (3) a2+2a+1 (4) 4x2-4x+1
解:(1)原式= x2+2·x 6+62=(x+6)2
(2)原式= -(x2+2xy+y2)=-(x+y)2
(3)原式=(a+1)2
(4)原式=(2x)2-2·2x·1+1=(2x-1)2
当堂检测
11.分解因式:
(1)?????2????2+????3; (2)????3?????10????2????+25????????;
(3)????2?52+85?????2+16; (4)(????2+????2?????2)2?4????2????2.
?
(1)解:?????2????2+????3=????1?2????+????2=?????????12;
?
(2)解:????3?????10????2????+25????????=????????(????2?10????+25)
=????????(?????5)2;
?
(3)解:????2?52+85?????2+16=????2?52?8????2?5+16
=????2?5?42=????2?92=????+32?????32
?
(4)解:=????2+????2?????2+2????????????2+????2?????2?2????????=????+????2?????2?????????2?????2
=????+????+????(????+?????????)(?????????+????)(??????????????).
?
当堂检测
解:
∵????2+????2+2?????4????+5=0,
∴????2+2????+1+????2?4????+4=0,
∴?(????+1)?+(????-2)?=0,
解得????=?1,????=2,
∴2????2+4?????3
=2×(-1)?+4×2?3
=2+8-3
=7.
?
12.已知????2+????2+2?????4????+5=0, 求2????2+4?????3 的值.
整式的乘法
与因式分解
八年级数学上册同步精品课堂(人教版)
人教版 数学
八年级 上册
14.3.2.2
运用完全平方
公式因式分解
复习回顾
(a+b)2=a2+2ab+b2,
我们把
(a-b)2=a2-2ab+b2.
都叫做完全平方公式.
文字语言:两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的 2 倍. 这两个公式叫做(乘法的)完全平方公式.
符号语言:
“首平方,尾平方,
积的 2 倍放中央.”
复习回顾
法二:借助几何图形证明:
如图,边长为(a+b) 的正方形的面积是(a+b)2 .
它的面积还可以视为两个小正方形和两个小长方形面积的和,
所以(a+b)2=a2+2ab+b2
b
a
a
b
a2
ab
ab
b2
即a2+ab+ab+b2=a2+2ab+b2 .
复习回顾
法二:借助几何图形证明:
它的面积还可以视为大正方形的面积减去两个小长方形面积的差,即
如图,边长为(a-b) 的正方形的面积是(a-b)2 .
所以(a-b)2=a2-2ab+b2.
(a-b)2
(a-b2)
a-b
b
b
a-b
ab
ab
b2
=a2-ab-ab+b2
=a2-2ab+b2
复习回顾
思考:
观察下面两个完全平方式,比一比,回答下列问题:
1. 说一说积的次数和项数;
2. 两个完全平方式的积有相同的项吗?与 a,b 有什么关系?
3. 两个完全平方式的积中不同的是哪一项?与 a,b 有什么关系?它的符号与什么有关?
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2.
公式中的字母 a,b 可以表示数,单项式和多项式.
积为二次三项式;
积中两项为两数的平方和;
另一项是两数积的 2 倍,且与两数中间的符号相同;
新知探究
思考:
对照 a? ± 2ab + b? = (a ± b)?,填空:
3. a? + 4ab + 4b? = ( )? + 2· ( ) ·( ) + ( )? = ( )?.
2. m? - 6m + 9 = ( )? - 2·( )·( ) + ( )? = ( )?;
1. x? + 4x + 4 = ( )? + 2·( )·( ) + ( )? = ( )?;
x
2
x + 2
a
a 2b
a + 2b
2b
m
m - 3
3
x
2
m
3
新知探究
思考:
下列各式是不是完全平方式?
(1)a2 - 4a + 4;
(2)1 + 4a?;
(3)4b2 + 4b - 1;
(4)a2 + ab + b2;
(5)x2 + x + 0.25.
是
(2)因为它只有两项.
不是
(3)4b? 与 -1 的符号不统一.
不是
不是
是
(4)因为 ab 不是 a 与 b 的积的 2 倍.
典例精析
例1
已知4????2+????????+36是完全平方式,则 m 的值为(??? ?)
A.8 B.±8 C.24 D.±24
?
【分析】解:∵4????2+????????+36是一个完全平方式,
∴mx=±2?2x?6,
解得:m=±24,
故选:D.
?
D
变式
若 x2 - 6x + N 是一个完全平方式,则 N = ( )
A . 11 B. 9 C. - 11 D. - 9
B
解析:根据完全平方式的特征,中间项 -6x = -2×x×3,故可知 N = 32 = 9.
典例精析
例2
(1)
4x2-4x+1
解:原式=
(2)
分解因式:
解:原式=
(3) -3a2x2 + 24a2x - 48a2;
=(a2 + 4 + 4a)(a2 + 4 - 4a)
解:(3) 原式=-3a2(x2 - 8x + 16)
=-3a2(x - 4)2.
(4) 原式=(a2 + 4)2 - (4a)2
=(a + 2)2(a - 2)2.
(4) (a2 + 4)2 - 16a2.
典例精析
例3
分解因式:
(1) ax2+2a2x+a3 (2) -3x2+6xy-3y2 (3) (x+y)2-12x-12y+36
解:(1)原式= a(x2+2ax+a2)=a(x+a)2
(3)原式=(x+y)2-12(x+y)+36
=(x+y)2-2·(x+y)·6+62
=(a+b-6)2
(2)原式= -3(x2-2xy+y2)=-3(x-y)2
典例精析
例4
(1) (x2+y2)2-4x2y2 (2)4x2(x-1)-16(1-x)2 (3)16x4-72x2+81
解: (1) 原式=(x2+y2+2xy)(x2+y2-2xy)=(x+y)2(x-y)2
(2)原式=4x2(x-1)-16(x-1)2=4(x-1)[x2-4(x-1)]
=4(x-1)(x2-4x+4)=4(x-1)(x-2)2
(3)原式=(4x2)2-2 · 4x2 · 9+92
= (4x2-9)2=[(2x+3)(2x-3)]2
=(2x+3)2(2x-3)2
分解因式:
典例精析
01
02
运用完全平方公式分解因式时,避免与平方差公式混淆.
03
运用完全平方公式分解因式时,有公因式应先提公因式.
运用完全平方公式分解因式时,应注意熟练把握公式的结构特征,避免出现符号、项数上的错误.
典例精析
例5
计算:
(1)3.142+6.28×6.86+6.862;(2)20222?2022×4042+20212.
?
解:(1)3.142+6.28×6.86+6.862
=3.142+2×3.14×6.86+6.862
=3.14+6.862
=102
=100.
?
(2)20222-2022×4042+20212
=20222-2×2022×2021+20212
=(2022-2021)2
=12
=1.
典例精析
例6
(1)已知a-b=3,求a(a-2b)+b2的值;
(2)已知ab=2,a+b=5,求a3b+2a2b2+ab3的值.
解:(1)原式=a2-2ab+b2=(a-b)2.
当a-b=3时,原式=32=9.
(2)原式=ab(a2+2ab+b2)=ab(a+b)2.
当ab=2,a+b=5时,
原式=2×52=50.
典例精析
例7
已知 a,b,c 分别是△ABC 三边的长,且 a2+2b2+c2-2b(a+c) = 0,请判断△ABC 的形状,并说明理由.
∴△ABC 是等边三角形.
解:由 a2+2b2+c2-2b(a+c) = 0,得
a2-2ab+b2+b2-2bc+c2 = 0,
即 (a-b)2+(b-c)2 = 0.
∴ a-b = 0,b-c = 0. ∴ a = b = c.
归纳总结
完全平方公式分解因式
公式
a2±2ab + b2 = (a±b)2
特点
(1)要求多项式有三项;
(2)其中两项是两个数或式的平方和,另一项则是这两数或式的乘积的 2 倍,符号可正可负
当堂检测
1.下列式子为完全平方式的是( )
A. a2+2a+b2 B. a2+2a+2 C. a2-2+b2 D. a2+2a+1.
2.分解因式x2-2x+1的最终结果是( )
A.x(x-2)+1 B. (x+1) (x-2) C. (x-1)2 D. (x+1)2
3.分解因式后结果是-(x-y)2的多项式是( )
A.-x2+2xy-y2 B. x2-2xy-y2 C. x2-2xy+y2 D. -x2-2xy-y2
D
C
A
4.下列分解因式错误的是( )
A. x2-y2= (x+y) (x-y) B. x2+6x+9= (x+3)2
C. x2+xy=x (x+y) D. x2+y2= (x+y)2
D
当堂检测
5.若x2- 2(k+1)x+4是完全平方式,则k的值为( )
A.1或-3 B. -1或3 C.±1 D.±3
6.已知????=????+2,则代数式3????2?6????????+3????2+2022的值为(???? )
A.2020 B.2024 C.2021 D.2034
?
A
D
7.分解因式????2+4????????+4????2?1=__________________________.
8.若x2﹣8x+m2=(x﹣4)2,那么m=_____.
9.若????2+(3?????)????+9可以用完全平方式来分解因式,则m的值为__________.
?
?????或9
?
????+????????+????)(????+?????????????
?
±????
?
当堂检测
10.分解因式:
(1) x2+12x+36 (2) -2xy-x2-y2 (3) a2+2a+1 (4) 4x2-4x+1
解:(1)原式= x2+2·x 6+62=(x+6)2
(2)原式= -(x2+2xy+y2)=-(x+y)2
(3)原式=(a+1)2
(4)原式=(2x)2-2·2x·1+1=(2x-1)2
当堂检测
11.分解因式:
(1)?????2????2+????3; (2)????3?????10????2????+25????????;
(3)????2?52+85?????2+16; (4)(????2+????2?????2)2?4????2????2.
?
(1)解:?????2????2+????3=????1?2????+????2=?????????12;
?
(2)解:????3?????10????2????+25????????=????????(????2?10????+25)
=????????(?????5)2;
?
(3)解:????2?52+85?????2+16=????2?52?8????2?5+16
=????2?5?42=????2?92=????+32?????32
?
(4)解:=????2+????2?????2+2????????????2+????2?????2?2????????=????+????2?????2?????????2?????2
=????+????+????(????+?????????)(?????????+????)(??????????????).
?
当堂检测
解:
∵????2+????2+2?????4????+5=0,
∴????2+2????+1+????2?4????+4=0,
∴?(????+1)?+(????-2)?=0,
解得????=?1,????=2,
∴2????2+4?????3
=2×(-1)?+4×2?3
=2+8-3
=7.
?
12.已知????2+????2+2?????4????+5=0, 求2????2+4?????3 的值.
