计算题特训:圆的周长与面积(易错专项)数学六年级上册人教版(含解析)
文档属性
| 名称 | 计算题特训:圆的周长与面积(易错专项)数学六年级上册人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 11:22:39 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
计算题特训:圆的周长与面积(易错专项)数学六年级上册人教版
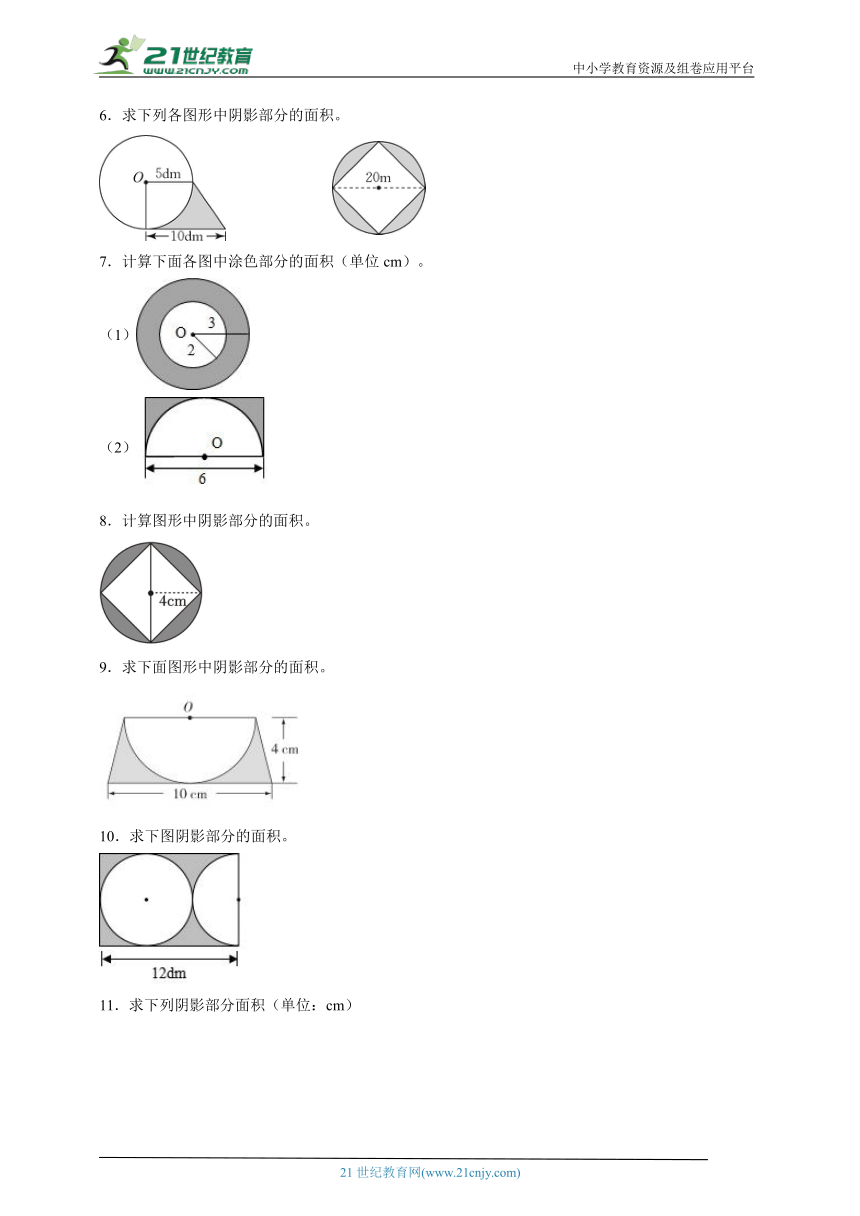
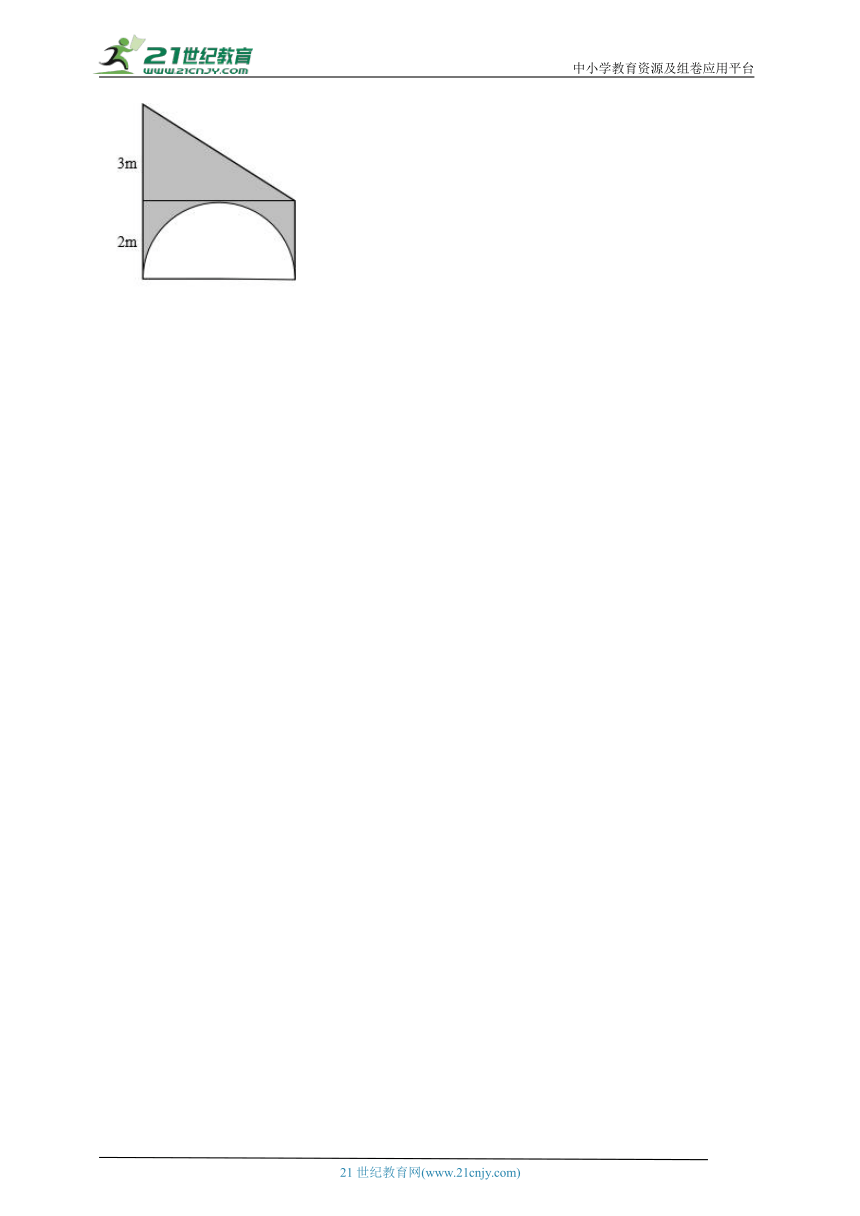
1.求阴影部分面积。()
2.求下面图形中阴影部分的周长和面积(单位:厘米)。
3.求出下面阴影部分的面积。
4.按要求计算。(单位:cm)
(1)计算图形的周长。
(2)计算阴影部分的面积。
5.求下图阴影部分的面积和周长。
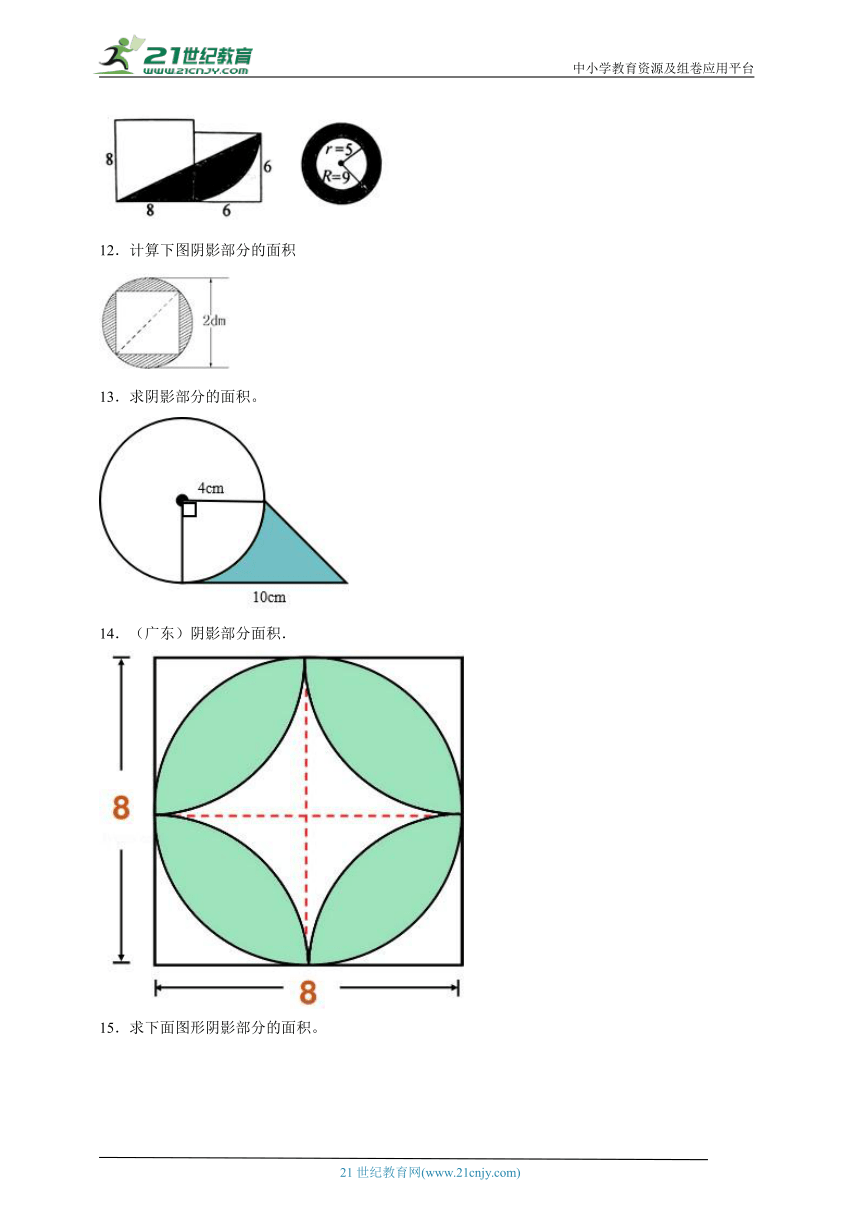
6.求下列各图形中阴影部分的面积。
7.计算下面各图中涂色部分的面积(单位cm)。
(1)
(2)
8.计算图形中阴影部分的面积。
9.求下面图形中阴影部分的面积。
10.求下图阴影部分的面积。
11.求下列阴影部分面积(单位:cm)
12.计算下图阴影部分的面积
13.求阴影部分的面积。
14.(广东)阴影部分面积.
15.求下面图形阴影部分的面积。
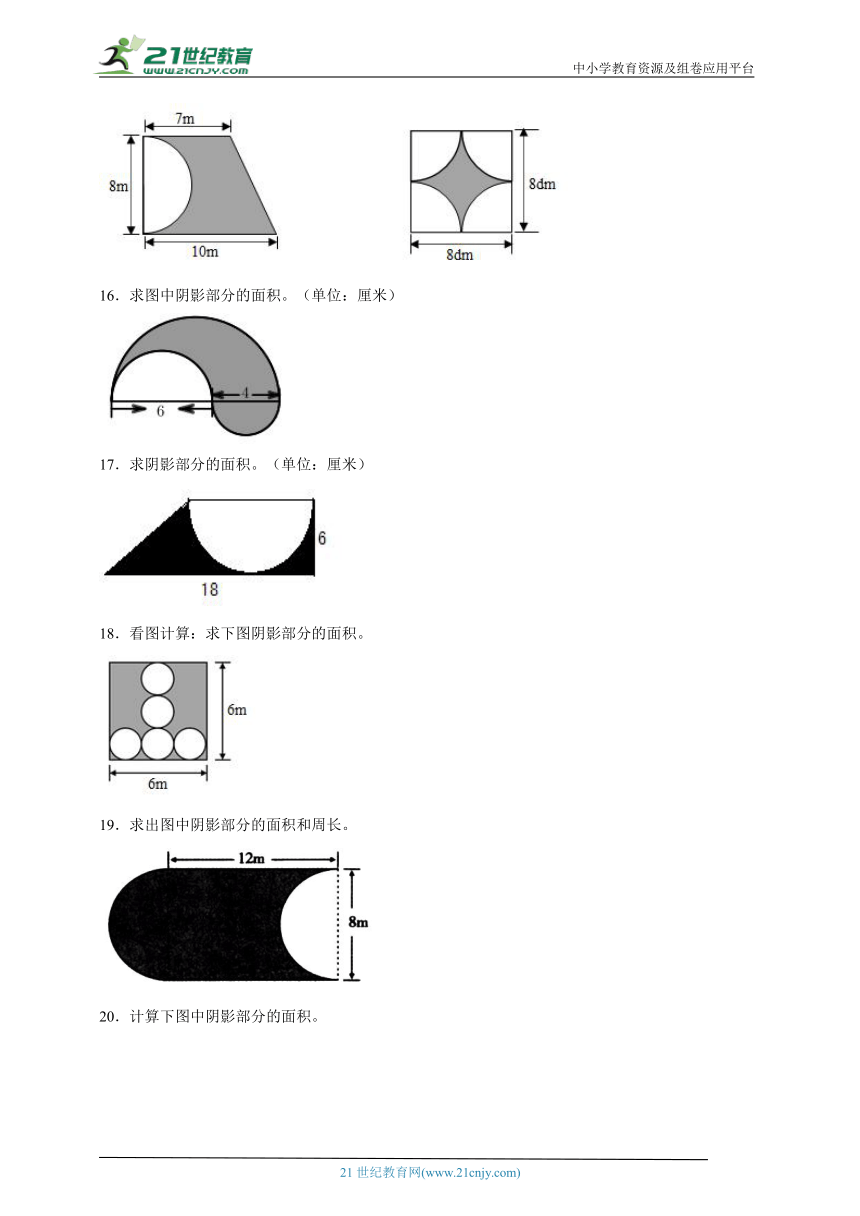
16.求图中阴影部分的面积。(单位:厘米)
17.求阴影部分的面积。(单位:厘米)
18.看图计算:求下图阴影部分的面积。
19.求出图中阴影部分的面积和周长。
20.计算下图中阴影部分的面积。
参考答案:
1.9.435dm2
【分析】观察图形可知,右边空白直角三角形的其中一个锐角是45°,所以该三角形是等腰直角三角形,它的两条直角边的长度都是4dm;左边圆的半径是3dm;整个图形是一个梯形,这个梯形的上底是3dm,下底是4dm,高是3+4=7dm,阴影部分的面积=梯形的面积-×半径是3dm圆的面积-右边空白三角形的面积,根据三角形的面积=底×高÷2,圆的面积公式:S=πr2,据此进行计算即可。
【详解】(3+4)×(3+4)÷2-×3.14×32-4×4÷2
=7×7÷2-×28.26-8
=24.5-7.065-8
=17.435-8
=9.435(dm2)
2.41.4厘米;39.25平方厘米
【分析】阴影部分的周长=大圆周长×+小圆周长×+10厘米;
阴影部分的面积=大圆面积×-小圆面积×。
【详解】2×3.14×10×+3.14×10×+10
=15.7+15.7+10
=41.4(厘米);
3.14×10 ×-3.14×(10÷2) ×
=78.5-39.25
=39.25(平方厘米)
3.4.86平方厘米
【分析】观察图形可知,圆的直径相当于长方形的宽,阴影部分的面积=长方形的面积-圆的面积,据此解答即可。
【详解】2×4-3.14×(2÷2)2
=8-3.14
=4.86(平方厘米)
4.(1)388.4厘米;
(2)0.86平方厘米
【分析】(1)图形周长=圆周长+两个100厘米的长,代入数据即可解答;
(2)阴影部分面积=正方形面积-圆面积。
【详解】(1)3.14×60+2×100
=188.4+200
=388.4(㎝)
(2)2×2-3.14×(2÷2)
=4-3.14
=0.86(平方厘米)
5.9平方厘米;15.42厘米
【分析】将图形分割移动如下:
此时阴影部分的面积等于底是6厘米,高是6÷2厘米的三角形的面积;
由图可知:阴影部分的周长=圆周长的一半+直径;据此解答。
【详解】6×(6÷2)÷2
=3×3
=9(平方厘米)
3.14×6÷2+6
=3.14×3+6
=9.42+6
=15.42(厘米)
6.17.875dm2 114m2
【详解】(5+10)×5÷2-3.14×52÷4=17.875(dm2)
3.14×(20÷2)2-20×(20÷2)÷2×2=3.14×100-200=114(m2)
7.(1)
(2)
【分析】(1)利用圆环的面积公式,求出涂色部分的面积。
(2)图中长方形的宽是3厘米,直径是6厘米,利用面积公式先算出长方形和半圆的面积,再用长方形的面积减去半圆的面积,即是涂色部分的面积。
【详解】(1)
(2)
8.18.24平方厘米
【分析】阴影部分的面积=圆的面积-空白部分正方形的面积,圆的直径等于正方形的对角线的长度。根据圆的面积公式:S=πr2,根据三角形的面积公式和正方形的面积公式,可得S=2r2,把数据代入公式解答。
【详解】3.14×42-2×4×4
=3.14×16-32
=50.24-32
=18.24(平方厘米)
阴影部分的面积是18.24平方厘米。
9.10.88平方厘米
【分析】从图中可看出,阴影部分的面积=梯形的面积-半圆的面积,根据梯形的面积公式和圆的面积公式,分别计算出梯形的面积和半圆的面积,再相减即可。
【详解】(4×2+10)×4÷2-3.14×42÷2
=18×4÷2-3.14×42÷2
=36-25.12
=10.88(平方厘米)
10.
【分析】观察可知,长方形的长=圆的半径×3,先确定圆的半径,阴影部分的面积=长方形面积-圆的面积-半圆的面积,圆的面积=πr2,据此列式计算。
【详解】
11.34.26cm2;175.84cm2
【分析】
第一题如图,阴影部分的面积=圆的面积-小三角形的面积+大三角形的面积,由此解答即可;第二题根据“”进行解答即可。
【详解】×3.14×6 -6×6÷2+8×6÷2
=28.26-18+24
=34.26(cm2);
3.14×(9 -5 )
=3.14×56
=175.84(cm2)
12.1.14dm2
【详解】3.14×(2÷2)2-2×(2÷2)÷2×2=1.14(dm2)
13.15.44平方厘米
【分析】阴影部分的面积=梯形的面积-圆面积的四分之一,据此解答即可。
【详解】
(平方厘米)
14.阴影部分的面积是36.48
【详解】试题分析:用正方形的面积减去半径为8÷2=4的圆的面积,就是中间空白部分的面积,再用直径是8的圆的面积减去空白部分的面积就是阴影部分的面积.
解答:解:8×8﹣3.14×(8÷2)2
=64﹣3.14×16
=64﹣50.24
=13.76
3.14×(8÷2)2﹣13.76
=3.14×16﹣13.73
=50.24﹣13.76
=36.48
答:阴影部分的面积是36.48.
点评: 在求不规则图形的面积时,要根据图形特征把它转化为几个规则图形的面积相加或相减的方法进行计算.
15.42.88平方米;13.76平方分米
【分析】(1)由图意可知:阴影部分面积=梯形面积-半圆面积,代入数据求解;
(2)根据上图可得:阴影部分面积=正方形面积-一个圆的面积,代入数据求解。
【详解】(1)(7+10)×8÷2-π×(8÷2) ÷2
=17×8÷2-16π÷2
=68-25.12
=42.88(平方米)
(2)8×8-π×(8÷2)
=64-50.24
=13.76(平方分米)
16.31.4平方厘米
【分析】图中有3个半圆,阴影部分的面积可以用直径为10的半圆的面积减去直径为6的半圆的面积,再加上直径为4的半圆的面积。
【详解】
17.33.48平方厘米
【分析】依题意可知,梯形的面积-半圆面积=阴影部分面积,据此解答。
【详解】(6×2+18)×6÷2-6 ÷2
=90-56.52
=33.48(平方厘米)
阴影部分的面积是33.48平方厘米。
18.20.3m2
【分析】根据正方形的边长计算出小圆的直径,进而算出半径,用正方形面积减去5个小圆的面积即可得到阴影部分的面积。
【详解】6×6-3.14×(6÷3÷2)2×5
=36-3.14×1×5
=36-15.7
=20.3(m2)
19.面积96m2;周长49.12m
【分析】
如图,把左边的阴影半圆向右平移到右边空白的半圆,这样阴影部分就是一个长12m、宽8m的长方形;根据长方形的面积=长×宽,代入数据计算,即可求出阴影部分的面积。
观察图形可知,阴影部分的周长=圆的周长+12×2,其中圆的周长公式C=πd,代入数据计算求解。
【详解】12×8=96(m2)
3.14×8+12×2
=25.12+24
=49.12(m)
阴影部分的面积是96m2,阴影部分的周长是49.12m。
20.7.72m2
【分析】由图可知,阴影部分的面积=梯形的面积-半圆的面积,根据梯形的面积=(上底+下底)×高÷2,半圆的面积=πr2÷2,代入数据进行解答即可。
【详解】(3+2+2)×(2×2)÷2-3.14×22÷2
=7×4÷2-3.14×4÷2
=14-12.56÷2
=14-6.28
=7.72(m2)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
计算题特训:圆的周长与面积(易错专项)数学六年级上册人教版
1.求阴影部分面积。()
2.求下面图形中阴影部分的周长和面积(单位:厘米)。
3.求出下面阴影部分的面积。
4.按要求计算。(单位:cm)
(1)计算图形的周长。
(2)计算阴影部分的面积。
5.求下图阴影部分的面积和周长。
6.求下列各图形中阴影部分的面积。
7.计算下面各图中涂色部分的面积(单位cm)。
(1)
(2)
8.计算图形中阴影部分的面积。
9.求下面图形中阴影部分的面积。
10.求下图阴影部分的面积。
11.求下列阴影部分面积(单位:cm)
12.计算下图阴影部分的面积
13.求阴影部分的面积。
14.(广东)阴影部分面积.
15.求下面图形阴影部分的面积。
16.求图中阴影部分的面积。(单位:厘米)
17.求阴影部分的面积。(单位:厘米)
18.看图计算:求下图阴影部分的面积。
19.求出图中阴影部分的面积和周长。
20.计算下图中阴影部分的面积。
参考答案:
1.9.435dm2
【分析】观察图形可知,右边空白直角三角形的其中一个锐角是45°,所以该三角形是等腰直角三角形,它的两条直角边的长度都是4dm;左边圆的半径是3dm;整个图形是一个梯形,这个梯形的上底是3dm,下底是4dm,高是3+4=7dm,阴影部分的面积=梯形的面积-×半径是3dm圆的面积-右边空白三角形的面积,根据三角形的面积=底×高÷2,圆的面积公式:S=πr2,据此进行计算即可。
【详解】(3+4)×(3+4)÷2-×3.14×32-4×4÷2
=7×7÷2-×28.26-8
=24.5-7.065-8
=17.435-8
=9.435(dm2)
2.41.4厘米;39.25平方厘米
【分析】阴影部分的周长=大圆周长×+小圆周长×+10厘米;
阴影部分的面积=大圆面积×-小圆面积×。
【详解】2×3.14×10×+3.14×10×+10
=15.7+15.7+10
=41.4(厘米);
3.14×10 ×-3.14×(10÷2) ×
=78.5-39.25
=39.25(平方厘米)
3.4.86平方厘米
【分析】观察图形可知,圆的直径相当于长方形的宽,阴影部分的面积=长方形的面积-圆的面积,据此解答即可。
【详解】2×4-3.14×(2÷2)2
=8-3.14
=4.86(平方厘米)
4.(1)388.4厘米;
(2)0.86平方厘米
【分析】(1)图形周长=圆周长+两个100厘米的长,代入数据即可解答;
(2)阴影部分面积=正方形面积-圆面积。
【详解】(1)3.14×60+2×100
=188.4+200
=388.4(㎝)
(2)2×2-3.14×(2÷2)
=4-3.14
=0.86(平方厘米)
5.9平方厘米;15.42厘米
【分析】将图形分割移动如下:
此时阴影部分的面积等于底是6厘米,高是6÷2厘米的三角形的面积;
由图可知:阴影部分的周长=圆周长的一半+直径;据此解答。
【详解】6×(6÷2)÷2
=3×3
=9(平方厘米)
3.14×6÷2+6
=3.14×3+6
=9.42+6
=15.42(厘米)
6.17.875dm2 114m2
【详解】(5+10)×5÷2-3.14×52÷4=17.875(dm2)
3.14×(20÷2)2-20×(20÷2)÷2×2=3.14×100-200=114(m2)
7.(1)
(2)
【分析】(1)利用圆环的面积公式,求出涂色部分的面积。
(2)图中长方形的宽是3厘米,直径是6厘米,利用面积公式先算出长方形和半圆的面积,再用长方形的面积减去半圆的面积,即是涂色部分的面积。
【详解】(1)
(2)
8.18.24平方厘米
【分析】阴影部分的面积=圆的面积-空白部分正方形的面积,圆的直径等于正方形的对角线的长度。根据圆的面积公式:S=πr2,根据三角形的面积公式和正方形的面积公式,可得S=2r2,把数据代入公式解答。
【详解】3.14×42-2×4×4
=3.14×16-32
=50.24-32
=18.24(平方厘米)
阴影部分的面积是18.24平方厘米。
9.10.88平方厘米
【分析】从图中可看出,阴影部分的面积=梯形的面积-半圆的面积,根据梯形的面积公式和圆的面积公式,分别计算出梯形的面积和半圆的面积,再相减即可。
【详解】(4×2+10)×4÷2-3.14×42÷2
=18×4÷2-3.14×42÷2
=36-25.12
=10.88(平方厘米)
10.
【分析】观察可知,长方形的长=圆的半径×3,先确定圆的半径,阴影部分的面积=长方形面积-圆的面积-半圆的面积,圆的面积=πr2,据此列式计算。
【详解】
11.34.26cm2;175.84cm2
【分析】
第一题如图,阴影部分的面积=圆的面积-小三角形的面积+大三角形的面积,由此解答即可;第二题根据“”进行解答即可。
【详解】×3.14×6 -6×6÷2+8×6÷2
=28.26-18+24
=34.26(cm2);
3.14×(9 -5 )
=3.14×56
=175.84(cm2)
12.1.14dm2
【详解】3.14×(2÷2)2-2×(2÷2)÷2×2=1.14(dm2)
13.15.44平方厘米
【分析】阴影部分的面积=梯形的面积-圆面积的四分之一,据此解答即可。
【详解】
(平方厘米)
14.阴影部分的面积是36.48
【详解】试题分析:用正方形的面积减去半径为8÷2=4的圆的面积,就是中间空白部分的面积,再用直径是8的圆的面积减去空白部分的面积就是阴影部分的面积.
解答:解:8×8﹣3.14×(8÷2)2
=64﹣3.14×16
=64﹣50.24
=13.76
3.14×(8÷2)2﹣13.76
=3.14×16﹣13.73
=50.24﹣13.76
=36.48
答:阴影部分的面积是36.48.
点评: 在求不规则图形的面积时,要根据图形特征把它转化为几个规则图形的面积相加或相减的方法进行计算.
15.42.88平方米;13.76平方分米
【分析】(1)由图意可知:阴影部分面积=梯形面积-半圆面积,代入数据求解;
(2)根据上图可得:阴影部分面积=正方形面积-一个圆的面积,代入数据求解。
【详解】(1)(7+10)×8÷2-π×(8÷2) ÷2
=17×8÷2-16π÷2
=68-25.12
=42.88(平方米)
(2)8×8-π×(8÷2)
=64-50.24
=13.76(平方分米)
16.31.4平方厘米
【分析】图中有3个半圆,阴影部分的面积可以用直径为10的半圆的面积减去直径为6的半圆的面积,再加上直径为4的半圆的面积。
【详解】
17.33.48平方厘米
【分析】依题意可知,梯形的面积-半圆面积=阴影部分面积,据此解答。
【详解】(6×2+18)×6÷2-6 ÷2
=90-56.52
=33.48(平方厘米)
阴影部分的面积是33.48平方厘米。
18.20.3m2
【分析】根据正方形的边长计算出小圆的直径,进而算出半径,用正方形面积减去5个小圆的面积即可得到阴影部分的面积。
【详解】6×6-3.14×(6÷3÷2)2×5
=36-3.14×1×5
=36-15.7
=20.3(m2)
19.面积96m2;周长49.12m
【分析】
如图,把左边的阴影半圆向右平移到右边空白的半圆,这样阴影部分就是一个长12m、宽8m的长方形;根据长方形的面积=长×宽,代入数据计算,即可求出阴影部分的面积。
观察图形可知,阴影部分的周长=圆的周长+12×2,其中圆的周长公式C=πd,代入数据计算求解。
【详解】12×8=96(m2)
3.14×8+12×2
=25.12+24
=49.12(m)
阴影部分的面积是96m2,阴影部分的周长是49.12m。
20.7.72m2
【分析】由图可知,阴影部分的面积=梯形的面积-半圆的面积,根据梯形的面积=(上底+下底)×高÷2,半圆的面积=πr2÷2,代入数据进行解答即可。
【详解】(3+2+2)×(2×2)÷2-3.14×22÷2
=7×4÷2-3.14×4÷2
=14-12.56÷2
=14-6.28
=7.72(m2)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
