立方根
图片预览

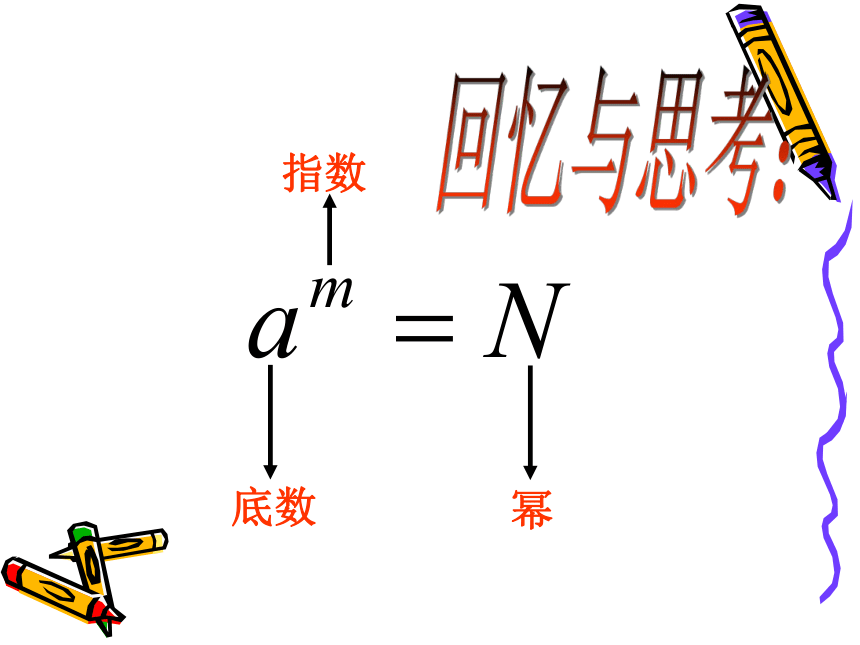








文档简介
课件32张PPT。13.2 立方根底数幂指数回忆与思考:由前面的学习可知:在式子 中
求括号里的数,这实际上是: 已知指数和幂求底数的运算,叫做开方运算。我们把括号里的±3叫做9的平方根(二次方根)。回忆与思考:±316的平方根是______-16的平方根是________0的平方根是________没有平方根0 一个正数有正负两个平方根,它们互为相反数;零的平方根是零,负数没有平方根.你还记得吗±4同理:若 这也是已知指数和幂求底数的运算,仍然叫做开方运算。我们把括号里的 3 叫做27的立方根(三次方根)。 一般地,如果 ,那么 叫 的立方根, 叫 的立方数。3数 的立方根用符号 表示。 读作:“三次根号 ”,其中 叫被开方数,3 是根指数。例如:∵∴ 5 是125 的立方根。也可以说,125 的立方根是 5 。用式子表示为: 注意: 的根指数 3 不能省略,要写在根
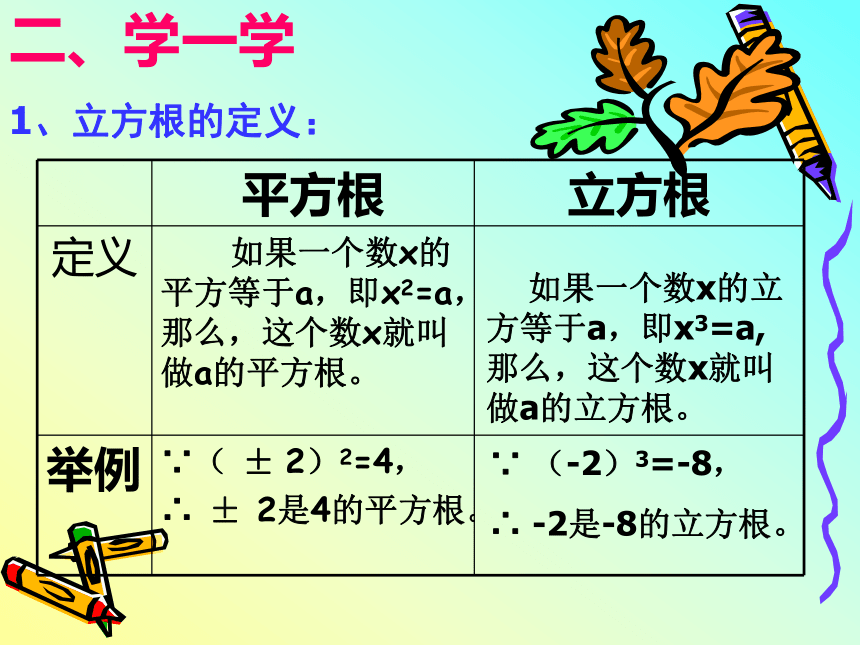
号的左上角,而且要写得小一些,不能写成 求一个数的立方根(三次方根)的运算,叫做开立方,开立方运算的结果就是立方根。因为开立方与立方互为逆运算。 所以我们可以运用立方运算来求一个数的立方根。定义: 如果一个数x的立方等于a,即x3=a,那么,这个数x就叫做a的立方根。 ∵ (-2)3=-8,
∴ -2是-8的立方根。二、学一学
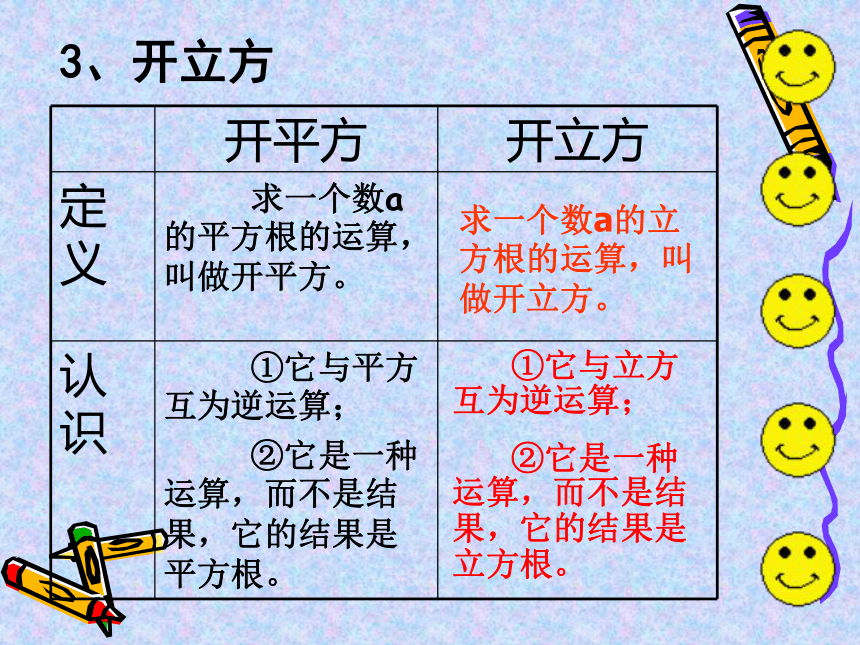
1、立方根的定义:2.立方根的性质探究1. 根据立方根的意义填空. 因为 =8,所以8的立方根是( ) 因为( ) =0.125,所以0.125的立方是( )因为( ) =0,所以0的立方根是( )因为 ( ) =-8,所以-8的立方根是( )因为( ) =- ,所以- 的立方( ) 02-20-2你能看出正数,0,负数的立方根各有什么特点?2、立方根的性质与表示 每个数都只有一个立方根。正数的立方根是正数;0的立方根是0;负数的立方根是负数。3、开立方求一个数a的立方根的运算,叫做开立方。 ①它与立方互为逆运算;
②它是一种运算,而不是结果,它的结果是立方根。例1:求下列各数的立方根。(1)-27; (2)27; (3)-0.216;
(4)0; (5)解:∵∴ -27的立方根是-3。即请你仿照上面的例子完成其余几个小题。被开方数立方根根指数注意:根指数是3 时,绝对不能省略不写。提醒你正数有立方根吗?如果有,有几个。想一想负数呢?零呢? 从上面的例1可知:一个正数有一个正的立方根;一个负数有一个负的立方根,零的立方根是零。由此得出求一个负数的立方根的一般方法: 也就是说,求一个负数的立方根,可以先求出这个负数的绝对值的立方根,然后再取它的相反数。 例2:求下列各式的值。解:(1)(1) ;(2) ;(3)
(4) (5)(2)(3)从上面的例题可知:由此可得出: 也就是把根号里的“负号”直接从根号里面提到了根号“外面” 。特别注意:平方根不能这样哟! 例2:求下列各式的值。解:(4)(1) ;(2) ;(3)
(4) (5)(5)探究先填写下表,再回答问题:0.010.1110100从上面表格中你发现什么?用计算器求125的立方根用计算器求1845的立方根
一个自然数的算术平方根是a,那么与这个自然数相邻的下一个自然数的平方根是______;立方根是________. 探究题课堂小结:相同点:
①0的平方根、立方根都有一个是0
②平方根、立方根都是开方的结果。
不同点:
①定义不同
②个数不同
③表示方法不同
④被开方数的取值范围不同1.立方根的定义,性质,计算.2.立方根与平方根的异同
(1)1的平方根是____;立方根为____;算术平方根为__.
(2)平方根是它本身的数是____.
(3)立方根是其本身的数是____.
(4)算术平方根是其本身的数是____.(5) 的立方根为 . (6) 的平方根为 . (7) 的立方根为 . 填空练习:11±100,±10, 1±2-2-21.判断下列说法是否正确,并说明理由:
(1) 的立方根是 ( )
(2)负数没有立方根 ( )
(3)4的平方根是2 ( )
(4)-8的立方根是-2 ( )
(5)立方根是它本身的数只有0 ( )
(6)互为相反数的数的立方根也互为相反数.( )
课堂练习1:√××××√3.求下列各数的立方根:
(1)1,(2)-1 ,(3) -0.000008 (4)3432.填空:-5-5解:例2、求下列各式的值:(1)(2)(3)解:(1)(2)(3)(4)21.分别求下列各式的值:课堂练习2:解:课堂练习2:2.你能求出下列各式中的未知数x吗?
(1) x3=343 (2)(x-1)3=125解:∴x=7∴x-1=5
X=6(3)(4)∴X=66∴x=81.一个正方体的体积变为原来的8倍,其边长变为原来的多少倍?2.一个正方体的体积变为原来的27倍,其边长变为原来的多少倍?3.一个正方体的体积变为原来的n(n>0)倍,其边长变为原来的多少倍?思考:4、一个正方体的体积变为原来的8倍,它的棱长变为原来的多少倍? 体积变为原来的27倍,它的棱长变为原来的多少倍? 体积变为原来的1000倍呢?试一试:一个正方体的体积变为原来的n倍,它的棱长变为原来的多少倍?1.分别求下列各式的值:作业2.你能求出下列各式中的未知数x吗?
(1) x3=343 (2)(x-1)3=1253、一个正方体的体积变为原来的8倍,它的棱长变为原来的多少倍? 体积变为原来的27倍,它的棱长变为原来的多少倍?n倍呢?
求括号里的数,这实际上是: 已知指数和幂求底数的运算,叫做开方运算。我们把括号里的±3叫做9的平方根(二次方根)。回忆与思考:±316的平方根是______-16的平方根是________0的平方根是________没有平方根0 一个正数有正负两个平方根,它们互为相反数;零的平方根是零,负数没有平方根.你还记得吗±4同理:若 这也是已知指数和幂求底数的运算,仍然叫做开方运算。我们把括号里的 3 叫做27的立方根(三次方根)。 一般地,如果 ,那么 叫 的立方根, 叫 的立方数。3数 的立方根用符号 表示。 读作:“三次根号 ”,其中 叫被开方数,3 是根指数。例如:∵∴ 5 是125 的立方根。也可以说,125 的立方根是 5 。用式子表示为: 注意: 的根指数 3 不能省略,要写在根
号的左上角,而且要写得小一些,不能写成 求一个数的立方根(三次方根)的运算,叫做开立方,开立方运算的结果就是立方根。因为开立方与立方互为逆运算。 所以我们可以运用立方运算来求一个数的立方根。定义: 如果一个数x的立方等于a,即x3=a,那么,这个数x就叫做a的立方根。 ∵ (-2)3=-8,
∴ -2是-8的立方根。二、学一学
1、立方根的定义:2.立方根的性质探究1. 根据立方根的意义填空. 因为 =8,所以8的立方根是( ) 因为( ) =0.125,所以0.125的立方是( )因为( ) =0,所以0的立方根是( )因为 ( ) =-8,所以-8的立方根是( )因为( ) =- ,所以- 的立方( ) 02-20-2你能看出正数,0,负数的立方根各有什么特点?2、立方根的性质与表示 每个数都只有一个立方根。正数的立方根是正数;0的立方根是0;负数的立方根是负数。3、开立方求一个数a的立方根的运算,叫做开立方。 ①它与立方互为逆运算;
②它是一种运算,而不是结果,它的结果是立方根。例1:求下列各数的立方根。(1)-27; (2)27; (3)-0.216;
(4)0; (5)解:∵∴ -27的立方根是-3。即请你仿照上面的例子完成其余几个小题。被开方数立方根根指数注意:根指数是3 时,绝对不能省略不写。提醒你正数有立方根吗?如果有,有几个。想一想负数呢?零呢? 从上面的例1可知:一个正数有一个正的立方根;一个负数有一个负的立方根,零的立方根是零。由此得出求一个负数的立方根的一般方法: 也就是说,求一个负数的立方根,可以先求出这个负数的绝对值的立方根,然后再取它的相反数。 例2:求下列各式的值。解:(1)(1) ;(2) ;(3)
(4) (5)(2)(3)从上面的例题可知:由此可得出: 也就是把根号里的“负号”直接从根号里面提到了根号“外面” 。特别注意:平方根不能这样哟! 例2:求下列各式的值。解:(4)(1) ;(2) ;(3)
(4) (5)(5)探究先填写下表,再回答问题:0.010.1110100从上面表格中你发现什么?用计算器求125的立方根用计算器求1845的立方根
一个自然数的算术平方根是a,那么与这个自然数相邻的下一个自然数的平方根是______;立方根是________. 探究题课堂小结:相同点:
①0的平方根、立方根都有一个是0
②平方根、立方根都是开方的结果。
不同点:
①定义不同
②个数不同
③表示方法不同
④被开方数的取值范围不同1.立方根的定义,性质,计算.2.立方根与平方根的异同
(1)1的平方根是____;立方根为____;算术平方根为__.
(2)平方根是它本身的数是____.
(3)立方根是其本身的数是____.
(4)算术平方根是其本身的数是____.(5) 的立方根为 . (6) 的平方根为 . (7) 的立方根为 . 填空练习:11±100,±10, 1±2-2-21.判断下列说法是否正确,并说明理由:
(1) 的立方根是 ( )
(2)负数没有立方根 ( )
(3)4的平方根是2 ( )
(4)-8的立方根是-2 ( )
(5)立方根是它本身的数只有0 ( )
(6)互为相反数的数的立方根也互为相反数.( )
课堂练习1:√××××√3.求下列各数的立方根:
(1)1,(2)-1 ,(3) -0.000008 (4)3432.填空:-5-5解:例2、求下列各式的值:(1)(2)(3)解:(1)(2)(3)(4)21.分别求下列各式的值:课堂练习2:解:课堂练习2:2.你能求出下列各式中的未知数x吗?
(1) x3=343 (2)(x-1)3=125解:∴x=7∴x-1=5
X=6(3)(4)∴X=66∴x=81.一个正方体的体积变为原来的8倍,其边长变为原来的多少倍?2.一个正方体的体积变为原来的27倍,其边长变为原来的多少倍?3.一个正方体的体积变为原来的n(n>0)倍,其边长变为原来的多少倍?思考:4、一个正方体的体积变为原来的8倍,它的棱长变为原来的多少倍? 体积变为原来的27倍,它的棱长变为原来的多少倍? 体积变为原来的1000倍呢?试一试:一个正方体的体积变为原来的n倍,它的棱长变为原来的多少倍?1.分别求下列各式的值:作业2.你能求出下列各式中的未知数x吗?
(1) x3=343 (2)(x-1)3=1253、一个正方体的体积变为原来的8倍,它的棱长变为原来的多少倍? 体积变为原来的27倍,它的棱长变为原来的多少倍?n倍呢?
