图形的相似第二课时教案(山东省东营市)
文档属性
| 名称 | 图形的相似第二课时教案(山东省东营市) |

|
|
| 格式 | rar | ||
| 文件大小 | 179.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-10-13 00:00:00 | ||
图片预览

文档简介
学习主题:27.1图形的相似(2)
学习目标:
1.掌握相似多边形的定义、表示法,并能根据定义判断两个多边形是否相似.
2.能根据相似比进行计算.
3.能根据定义判断两个多边形是否相似,训练学生的判断能力.
4.能根据相似比求长度和角度,培养学生的运用能力.
学习过程:
一 知识回顾
1、相似图形的定义:
二 问题引入
1、思考:
(1)、下图是两个等边三角形,它们相似吗 它们的对应角、对应边分别有什么关系
答:
文字叙述: 。
(2)、思考:下图是两个正六边形,它们相似吗 它们的对应角、对应边分别有什么关系
答:
总结:从上述两个问题的探索中你能得到什么结论
答:
2、任意两个相似三角形,它们的对应角、对应边有上面的结论吗?
答:
结论:任意两个相似三角形,它们的对应角 、对应边 。
3、图中两个四边形是相似形,仔细观察这两个图形,它们的对应边之间是否有以上的关系呢?对应角之间又有什么关系?
答:
结论:任意两个相似多边形,它们的对应角 、对应边 。
由此,我们得到了:
相似多边形的性质: 。
相似多边形的判定: 。
并且相似多边形对应边的比叫 。
三 经典例题
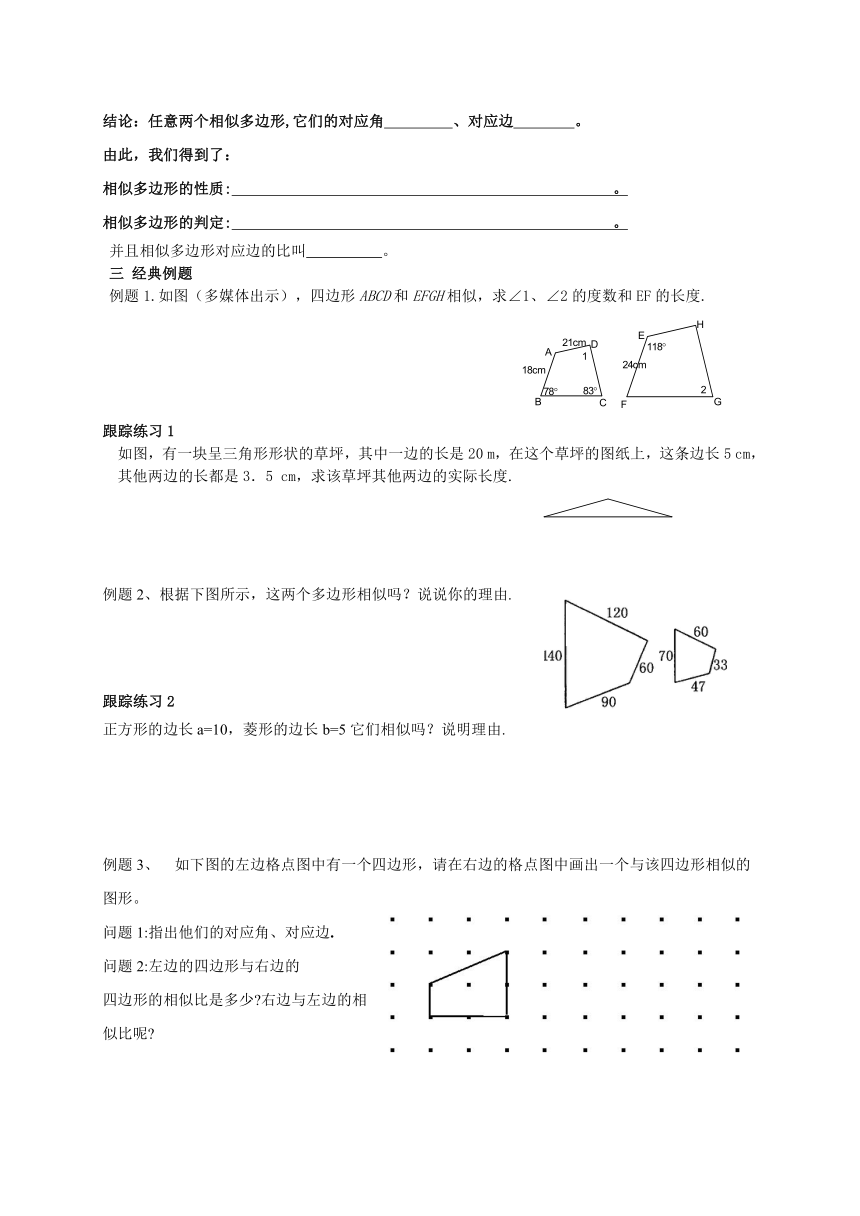
例题1.如图(多媒体出示),四边形ABCD和EFGH相似,求∠1、∠2的度数和EF的长度.
跟踪练习1
如图,有一块呈三角形形状的草坪,其中一边的长是20 m,在这个草坪的图纸上,这条边长5 cm,其他两边的长都是3.5 cm,求该草坪其他两边的实际长度.
例题2、根据下图所示,这两个多边形相似吗?说说你的理由.
跟踪练习2
正方形的边长a=10,菱形的边长b=5它们相似吗?说明理由.
例题3、 如下图的左边格点图中有一个四边形,请在右边的格点图中画出一个与该四边形相似的图形。
问题1:指出他们的对应角、对应边.
问题2:左边的四边形与右边的
四边形的相似比是多少 右边与左边的相似比呢
四 基础演练
1.判断题
⑴两个菱形是相似形. ( )
⑵两个矩形是相似形. ( )
⑶两个正方形是相似形. ( )
⑷两个正多边形是相似形. ( )
⑸有一个角相等的两个等腰梯形是相似形 .( )
⑹两个直角梯形是相似形. ( )
2.点P在线段AB上,且AP∶PB=2∶5,则AB∶PB= ,AP∶AB= .
3.某市城市广场,是一个因周边环境设计建造的一个不规则多边形,具有和谐的自然美.设计图的比例尺是1∶10 000.则图上多边形与实际多边形的相似比是 .
4.下列图形中,必是相似形的是( )
A.都有一个角是40 的两个等腰三角形 B.都有一个角为50 的两个等腰梯形
C.都有一个角是30 的两个菱形 D.邻边之比为2:3的两个平行四边形.
5.如图,有三个矩形,其中相似的是( )
A.甲和乙 B.甲和丙
C.乙和丙 D.没有相似的矩形
6.一个四边形的各边长分别为1 cm,2 cm,3 cm,4 cm,另一个与它相似的四边形的周长是40 cm那么后一个四边形的最长边的长是( )
A.1 cm. B. 4 cm. C. 10 cm. D.16 cm.
7.请在方格子内画出一个与已知图形相似的图形.
8.如图,四边形ABCD∽四边形A′B′C′D′,∠A=∠A ′=55°, ∠B=65 ° ,∠D ′=128°,AD=12,A′D′=6,A′B′=10,B′C′=8.求∠ C′的大小和AB,BC的长度.
9.在边长分别为6和13的矩形的较长边上取一点,作平行于另一边的直线将它分为两个小矩形,尽寸如图,求证这两个小矩形相似.
10.在一矩形ABCD的花坛四周修筑小路,使得相对两条小路的宽均相等。花坛AB=20米,AD=30米,试问小路的宽x与y的比值为多少时,能使小路四周所围成的矩形A`B`C`D`能与矩形ABCD相似?请说明理由。
五 拓展平台
1.把一张矩形的纸片对折后和原矩形相似,则那么大矩形与小矩形的相似比是 ( )
A.:1 B.2:1 C.3:1 D.4:1
2.观察下列一组图形,图形中的三角形都是相似图形,根据其变化规律,可得第10个图形中三角形的个数为_________
3.如图,在矩形ABCD中,EF‖BC,GH‖AB,EF与GH交于点H,且AE=1,AG=CF=2,CH=4,你能找出图中共有几对相似矩形吗?若能,请选择其中的一对证明。
7.如果梯形ABCD的各边向外平移2个单位得到新的梯形A`B`C`D`,试问图中的两个梯形能相似吗?请说明理由。
2
4
1
图1
图3
2
0
D
A
B
C
E
G
F
H
学习目标:
1.掌握相似多边形的定义、表示法,并能根据定义判断两个多边形是否相似.
2.能根据相似比进行计算.
3.能根据定义判断两个多边形是否相似,训练学生的判断能力.
4.能根据相似比求长度和角度,培养学生的运用能力.
学习过程:
一 知识回顾
1、相似图形的定义:
二 问题引入
1、思考:
(1)、下图是两个等边三角形,它们相似吗 它们的对应角、对应边分别有什么关系
答:
文字叙述: 。
(2)、思考:下图是两个正六边形,它们相似吗 它们的对应角、对应边分别有什么关系
答:
总结:从上述两个问题的探索中你能得到什么结论
答:
2、任意两个相似三角形,它们的对应角、对应边有上面的结论吗?
答:
结论:任意两个相似三角形,它们的对应角 、对应边 。
3、图中两个四边形是相似形,仔细观察这两个图形,它们的对应边之间是否有以上的关系呢?对应角之间又有什么关系?
答:
结论:任意两个相似多边形,它们的对应角 、对应边 。
由此,我们得到了:
相似多边形的性质: 。
相似多边形的判定: 。
并且相似多边形对应边的比叫 。
三 经典例题
例题1.如图(多媒体出示),四边形ABCD和EFGH相似,求∠1、∠2的度数和EF的长度.
跟踪练习1
如图,有一块呈三角形形状的草坪,其中一边的长是20 m,在这个草坪的图纸上,这条边长5 cm,其他两边的长都是3.5 cm,求该草坪其他两边的实际长度.
例题2、根据下图所示,这两个多边形相似吗?说说你的理由.
跟踪练习2
正方形的边长a=10,菱形的边长b=5它们相似吗?说明理由.
例题3、 如下图的左边格点图中有一个四边形,请在右边的格点图中画出一个与该四边形相似的图形。
问题1:指出他们的对应角、对应边.
问题2:左边的四边形与右边的
四边形的相似比是多少 右边与左边的相似比呢
四 基础演练
1.判断题
⑴两个菱形是相似形. ( )
⑵两个矩形是相似形. ( )
⑶两个正方形是相似形. ( )
⑷两个正多边形是相似形. ( )
⑸有一个角相等的两个等腰梯形是相似形 .( )
⑹两个直角梯形是相似形. ( )
2.点P在线段AB上,且AP∶PB=2∶5,则AB∶PB= ,AP∶AB= .
3.某市城市广场,是一个因周边环境设计建造的一个不规则多边形,具有和谐的自然美.设计图的比例尺是1∶10 000.则图上多边形与实际多边形的相似比是 .
4.下列图形中,必是相似形的是( )
A.都有一个角是40 的两个等腰三角形 B.都有一个角为50 的两个等腰梯形
C.都有一个角是30 的两个菱形 D.邻边之比为2:3的两个平行四边形.
5.如图,有三个矩形,其中相似的是( )
A.甲和乙 B.甲和丙
C.乙和丙 D.没有相似的矩形
6.一个四边形的各边长分别为1 cm,2 cm,3 cm,4 cm,另一个与它相似的四边形的周长是40 cm那么后一个四边形的最长边的长是( )
A.1 cm. B. 4 cm. C. 10 cm. D.16 cm.
7.请在方格子内画出一个与已知图形相似的图形.
8.如图,四边形ABCD∽四边形A′B′C′D′,∠A=∠A ′=55°, ∠B=65 ° ,∠D ′=128°,AD=12,A′D′=6,A′B′=10,B′C′=8.求∠ C′的大小和AB,BC的长度.
9.在边长分别为6和13的矩形的较长边上取一点,作平行于另一边的直线将它分为两个小矩形,尽寸如图,求证这两个小矩形相似.
10.在一矩形ABCD的花坛四周修筑小路,使得相对两条小路的宽均相等。花坛AB=20米,AD=30米,试问小路的宽x与y的比值为多少时,能使小路四周所围成的矩形A`B`C`D`能与矩形ABCD相似?请说明理由。
五 拓展平台
1.把一张矩形的纸片对折后和原矩形相似,则那么大矩形与小矩形的相似比是 ( )
A.:1 B.2:1 C.3:1 D.4:1
2.观察下列一组图形,图形中的三角形都是相似图形,根据其变化规律,可得第10个图形中三角形的个数为_________
3.如图,在矩形ABCD中,EF‖BC,GH‖AB,EF与GH交于点H,且AE=1,AG=CF=2,CH=4,你能找出图中共有几对相似矩形吗?若能,请选择其中的一对证明。
7.如果梯形ABCD的各边向外平移2个单位得到新的梯形A`B`C`D`,试问图中的两个梯形能相似吗?请说明理由。
2
4
1
图1
图3
2
0
D
A
B
C
E
G
F
H
