苏科版九年级数学下册 7.5解直角三角形 同步练习题 (含解析)
文档属性
| 名称 | 苏科版九年级数学下册 7.5解直角三角形 同步练习题 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 726.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 11:24:48 | ||
图片预览




文档简介
苏科版九年级数学下册《7.5解直角三角形》同步练习题
一、单选题
1.Rt△ABC的边长都扩大2倍,则的值( )
A.不变 B.变大 C.变小 D.无法判断
2.在中,,,,则的度数是( )
A. B. C. D.
3.如图,已知在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足是D,设∠CAB=α,CD=h,那么BC的长度为( )
A. B. C. D.h cosα
4.在Rt△ABC中,∠C=90°,∠ABC=45°,延长CB到D,BD=AB,连接AD,得∠D=22.5°,根据此图可求得tan22.5°的结果为( )
A. B. C. D.
5.如图,是线段AB在投影面P上的正投影,,,则投影的长为( )
A. B. C. D.
6.如图,网格中小正方形的边长均为1,△ABC的顶点都在格点上,则cos∠BAC等于( )
A. B. C. D.
7.如图,△ABC内接于⊙O,AD是直径.若,,则AD的长为( )
A.10 B.8 C.4 D.2
8.如图,已知第一象限内的点A在反比例函数的图象上,第二象限的点B在反比例函数的图象上,且,则k的值为( )
A. B. C. D.
二、填空题
9.已知一个正六边形的边心距为,则它的半径为 .
10.如图,在中,,,D为上一点,将沿折叠后,点C恰好落在斜边的中点E处,则折痕的长为 .
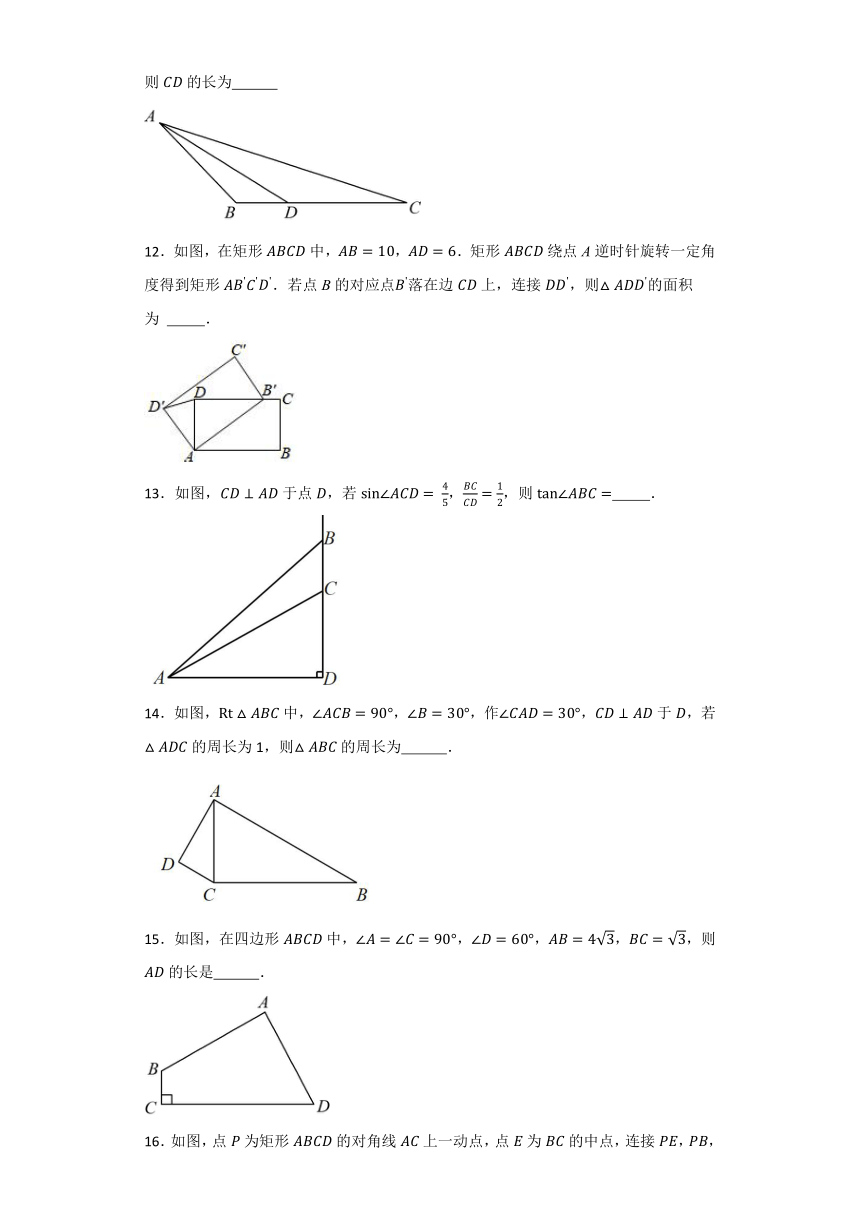
11.如图,中,平分,,,,则的长为
12.如图,在矩形中,,.矩形绕点A逆时针旋转一定角度得到矩形.若点B的对应点落在边上,连接,则的面积为 .
13.如图,于点,若 ,,则 .
14.如图,中,,,作,于,若的周长为1,则的周长为 .
15.如图,在四边形中,,,,,则的长是 .
16.如图,点为矩形的对角线上一动点,点为的中点,连接,,若,,则的最小值为 .
三、解答题
17.在中,,,,则的面积为多少?
18.已知中,,.
(1)如图1,若,求的长.
(2)如图2,若,求的长.
19.如图,在正方形中,为上一点,连接,,交于点,交的延长线于点.
(1)求证:.
(2)若,,求的面积.
20.如图,是的直径,点,在上,,与相交于点,点在的延长线上,且.
(1)求证:是的切线;
(2)若,,求的半径.
21.在中,点为弦上一点,连接,为优弧上的点,平分.
(1)如图1,求证;
(2)如图2,延长交于点,连接,若,,求的值;
(3)如图3,在(2)的条件下,若,,求线段的长.
22.【问题情境】如图,在中,,.点D在边上将线段绕点D顺时针旋转得到线段(旋转角小于),连接,,以为底边在其上方作等腰三角形,使,连接.
【尝试探究】
(1)如图1,当时,易知;
如图2,当时,则与的数量关系为 ;
(2)如图3,写出与的数量关系(用含α的三角函数表示).并说明理由;
【拓展应用】
(3)如图4,当,且点B,E,F三点共线时.若,,请直接写出的长.
参考答案
1.解:∵Rt△ABC的边长都扩大2倍,
∴所得的三角形与原三角形相似,
∴∠A的大小没有发生变化,
∴sinA的值不变,
故选:A.
2.解:如图所示:
∵BC=3,AC=,∠C=90°,
∴,
∴∠A=60°.
故选:D.
3.解:∵CD⊥AB,
∴∠CAD+∠DCA=90°,
∵∠ACB=∠ACD+∠BCD=90°,
∴∠BCD=∠CAD=α,
在Rt△BCD中,
∵cos∠BCD=,CD=h,
∴BC=.
故选:B.
4.解:∵在Rt△ABC中,∠C=90°,∠ABC=45°,
∴∠BAC=45°=∠ABC,
∴AC=BC,
设AC=BC=1,则,
∴,
∴,
∴,
故选B.
5.解:过点A作于点C,
四边形是矩形,
,
在中,,
,
故选:A.
6.解:∵小正方形的边长均为1,
∴,
∴,
∴△ABC是直角三角形,且∠ACB=90°,
∴cos∠BAC=.
故选:C.
7.解:连接CD,
∵∠B与∠D所对的弧都是,
∴,
∵AD是直径,
∴,
∵AC=6,
∴,
∴,
故选:C
8.解:作轴于C,轴于D,如图,
则,
在中,,
∵,
∴,
∴,
∴,
∴,
∴,
而,
∴.
故选:C.
9.解:如图,过O作与G,
∵,,
∴,
在中,,,
∴,
故答案为:2.
10.解:方法一:∵将沿折叠后,点C恰好落在斜边的中点E处,
∴,,,
∴,,
∴.
又∵,
∴,
∵,
∴.
方法二:在中, ,
设,则,
∴.
在中,,
即,
解得,
即.
故答案为:
11.解:如图所示,过点作交点延长线于点,过点作于点,
∵平分,
∴,
∵,
设,则,,
∴,
∴,
延长,交于点,
∴,
∴是等腰直角三角形,
∴,
∵,平分,
∴,
∴垂直平分,
∴,
∴,
∴,
∴,
∵,
设,则,
∴,
∵,
∴,
∴,
∴,
解得:,
∴,
故答案为:.
12.解:如图,过点作于点E,
∵,,由旋转的性质可得,
在中,由勾股定理可得,
又∵,
∴,
∴,
∴,
∴,
在中,由勾股定理,得,
∴.
故答案为:.
13.解:,
,
,
∵,
,
,
,
,
,
故答案为.
14.解:中,,,
,
,,
,于,
在中,,
,,
的周长为,
,
即,
的周长为 .
故答案为:.
15.解:延长与相交于点E,在中,
∵,
∴.
在中,∵ ,
∴,
∴
在中,∵,
故答案为6
16.解:作点关于的对称点,交于点,连接交于点,则的最小值为的长度,
∵是矩形的对角线,
∴,,
在直角中,,,
∴,
∴,
由对称的性质,得,,
∴,
∴
∵,,
∴是等边三角形,
∴,
∴是直角三角形,
∴,
∴的最小值为,
故答案为:.
17.解:如图,过点B作,交于点D,
在中,,
设,则,
在中,,
∴,
在中,,
即,解得(负值舍去),
∴,
∴.
18.(1)解:中,,
,,
,
,
;
(2)解:在中,,
,
,,
,
.
19.(1)证明:四边形是正方形,
,
,
,
,
,
;
(2) ,
,
四边形是正方形,,
,,,
,
,
,
,
,
,即,
,即,
,
,
.
20.(1)证明:∵为的直径,
∴,
∴,
∴,
∵,
∴,
∵,
∵,
∴弧弧,
∴,
∴,
∴,
∴,
∴是的切线.
(2)解:∵,,
∴,
∴,
∴,
∵,
设,,
∴在中,,
∵,,,
∴,
∴,
∵,
∴,
∴半径 ,
21.(1)证明:如图,过点O作,,垂足为点,连接,
则.
∵平分,
∴,
在与中,,
∴,
∴.
在与中,,
∴,
∴,
∴,
即;
(2)解:如图,经过作直径,交于点G.连接、、、.
∵,,
∴,
∴,
即,
设圆半径为r,设,,则,,
∴,,
∴,
解得:,
∵平分,,
∴.
在和中,设,,由勾股定理得:
,,
∴,
解得:,.
在中,,
∵,
∴,
∵,
∴,
∴;
(3)解:如图,连接,,,,
设,由(2)可得,,
则,
∴ ,
∴,
由(1)可得,
∴是等边三角形,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
又,
∴,
∴,
∴,
∴,
延长交于点,
则,,
则是等边三角形,
过点作于点, 于点,,交于点,连接,
∵是等边三角形,
∴,,
∵,,
∴是的重心,
∴,
在中,,,,
∴,
∴,
解得:,
∴.
22.解:(1)如图,过点A作于点H,
∵,,
∴,
∴.
∵是以为底边的等腰三角形,,
∴,.
∴.
∴.
∴.
∴.
∴.
∵,
∴.
∴.
∴.
∵,H为的中点,
∴.
在中,,
∴.
∴.
∴.
又,
∴;
(2)解:;
如图,过点A作于点H,
∵,,
∴,
∴.
∵是以为底边的等腰三角形,,
∴,.
∴.
∴.
∴.
∴.
∴.
∵,
∴.
∴.
∴.
∵,H为的中点,
∴.
在中,,
∴.
∴.
∴.
(3).
方法一:
如图,过点D作于点M,过点C作,交延长线于点H,
∴.
∴.
∵线段绕点D顺时针旋转得到线段,
∴.
∴.
∵是以为底边的等腰三角形,,
∴,.
∴.
∴.
∴.
∵,
∴.
设,则,
∵,
∴,
∴.
∴.
∵,
∴,.
∴.
在中,,,
∴.
∴,解得.
∴.
∵,
∴.
方法二:
如图,过点C作交延长线于点G,过点D作于点M,过点E作于点H,
∴.
∴.
∵线段绕点D顺时针旋转得到线段,
∴.
∴.
∵,
∴,.
∴.
∵,
∴.
∵是以为底边的等腰三角形,,
∴.
∵,
∴,.
∴.
设,则,
∵,
∴.
∴.
∴.
∴.
在中,,
∴.
在中,,,
∴.
∴,解得.
∴.
∵,
∴.
一、单选题
1.Rt△ABC的边长都扩大2倍,则的值( )
A.不变 B.变大 C.变小 D.无法判断
2.在中,,,,则的度数是( )
A. B. C. D.
3.如图,已知在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足是D,设∠CAB=α,CD=h,那么BC的长度为( )
A. B. C. D.h cosα
4.在Rt△ABC中,∠C=90°,∠ABC=45°,延长CB到D,BD=AB,连接AD,得∠D=22.5°,根据此图可求得tan22.5°的结果为( )
A. B. C. D.
5.如图,是线段AB在投影面P上的正投影,,,则投影的长为( )
A. B. C. D.
6.如图,网格中小正方形的边长均为1,△ABC的顶点都在格点上,则cos∠BAC等于( )
A. B. C. D.
7.如图,△ABC内接于⊙O,AD是直径.若,,则AD的长为( )
A.10 B.8 C.4 D.2
8.如图,已知第一象限内的点A在反比例函数的图象上,第二象限的点B在反比例函数的图象上,且,则k的值为( )
A. B. C. D.
二、填空题
9.已知一个正六边形的边心距为,则它的半径为 .
10.如图,在中,,,D为上一点,将沿折叠后,点C恰好落在斜边的中点E处,则折痕的长为 .
11.如图,中,平分,,,,则的长为
12.如图,在矩形中,,.矩形绕点A逆时针旋转一定角度得到矩形.若点B的对应点落在边上,连接,则的面积为 .
13.如图,于点,若 ,,则 .
14.如图,中,,,作,于,若的周长为1,则的周长为 .
15.如图,在四边形中,,,,,则的长是 .
16.如图,点为矩形的对角线上一动点,点为的中点,连接,,若,,则的最小值为 .
三、解答题
17.在中,,,,则的面积为多少?
18.已知中,,.
(1)如图1,若,求的长.
(2)如图2,若,求的长.
19.如图,在正方形中,为上一点,连接,,交于点,交的延长线于点.
(1)求证:.
(2)若,,求的面积.
20.如图,是的直径,点,在上,,与相交于点,点在的延长线上,且.
(1)求证:是的切线;
(2)若,,求的半径.
21.在中,点为弦上一点,连接,为优弧上的点,平分.
(1)如图1,求证;
(2)如图2,延长交于点,连接,若,,求的值;
(3)如图3,在(2)的条件下,若,,求线段的长.
22.【问题情境】如图,在中,,.点D在边上将线段绕点D顺时针旋转得到线段(旋转角小于),连接,,以为底边在其上方作等腰三角形,使,连接.
【尝试探究】
(1)如图1,当时,易知;
如图2,当时,则与的数量关系为 ;
(2)如图3,写出与的数量关系(用含α的三角函数表示).并说明理由;
【拓展应用】
(3)如图4,当,且点B,E,F三点共线时.若,,请直接写出的长.
参考答案
1.解:∵Rt△ABC的边长都扩大2倍,
∴所得的三角形与原三角形相似,
∴∠A的大小没有发生变化,
∴sinA的值不变,
故选:A.
2.解:如图所示:
∵BC=3,AC=,∠C=90°,
∴,
∴∠A=60°.
故选:D.
3.解:∵CD⊥AB,
∴∠CAD+∠DCA=90°,
∵∠ACB=∠ACD+∠BCD=90°,
∴∠BCD=∠CAD=α,
在Rt△BCD中,
∵cos∠BCD=,CD=h,
∴BC=.
故选:B.
4.解:∵在Rt△ABC中,∠C=90°,∠ABC=45°,
∴∠BAC=45°=∠ABC,
∴AC=BC,
设AC=BC=1,则,
∴,
∴,
∴,
故选B.
5.解:过点A作于点C,
四边形是矩形,
,
在中,,
,
故选:A.
6.解:∵小正方形的边长均为1,
∴,
∴,
∴△ABC是直角三角形,且∠ACB=90°,
∴cos∠BAC=.
故选:C.
7.解:连接CD,
∵∠B与∠D所对的弧都是,
∴,
∵AD是直径,
∴,
∵AC=6,
∴,
∴,
故选:C
8.解:作轴于C,轴于D,如图,
则,
在中,,
∵,
∴,
∴,
∴,
∴,
∴,
而,
∴.
故选:C.
9.解:如图,过O作与G,
∵,,
∴,
在中,,,
∴,
故答案为:2.
10.解:方法一:∵将沿折叠后,点C恰好落在斜边的中点E处,
∴,,,
∴,,
∴.
又∵,
∴,
∵,
∴.
方法二:在中, ,
设,则,
∴.
在中,,
即,
解得,
即.
故答案为:
11.解:如图所示,过点作交点延长线于点,过点作于点,
∵平分,
∴,
∵,
设,则,,
∴,
∴,
延长,交于点,
∴,
∴是等腰直角三角形,
∴,
∵,平分,
∴,
∴垂直平分,
∴,
∴,
∴,
∴,
∵,
设,则,
∴,
∵,
∴,
∴,
∴,
解得:,
∴,
故答案为:.
12.解:如图,过点作于点E,
∵,,由旋转的性质可得,
在中,由勾股定理可得,
又∵,
∴,
∴,
∴,
∴,
在中,由勾股定理,得,
∴.
故答案为:.
13.解:,
,
,
∵,
,
,
,
,
,
故答案为.
14.解:中,,,
,
,,
,于,
在中,,
,,
的周长为,
,
即,
的周长为 .
故答案为:.
15.解:延长与相交于点E,在中,
∵,
∴.
在中,∵ ,
∴,
∴
在中,∵,
故答案为6
16.解:作点关于的对称点,交于点,连接交于点,则的最小值为的长度,
∵是矩形的对角线,
∴,,
在直角中,,,
∴,
∴,
由对称的性质,得,,
∴,
∴
∵,,
∴是等边三角形,
∴,
∴是直角三角形,
∴,
∴的最小值为,
故答案为:.
17.解:如图,过点B作,交于点D,
在中,,
设,则,
在中,,
∴,
在中,,
即,解得(负值舍去),
∴,
∴.
18.(1)解:中,,
,,
,
,
;
(2)解:在中,,
,
,,
,
.
19.(1)证明:四边形是正方形,
,
,
,
,
,
;
(2) ,
,
四边形是正方形,,
,,,
,
,
,
,
,
,即,
,即,
,
,
.
20.(1)证明:∵为的直径,
∴,
∴,
∴,
∵,
∴,
∵,
∵,
∴弧弧,
∴,
∴,
∴,
∴,
∴是的切线.
(2)解:∵,,
∴,
∴,
∴,
∵,
设,,
∴在中,,
∵,,,
∴,
∴,
∵,
∴,
∴半径 ,
21.(1)证明:如图,过点O作,,垂足为点,连接,
则.
∵平分,
∴,
在与中,,
∴,
∴.
在与中,,
∴,
∴,
∴,
即;
(2)解:如图,经过作直径,交于点G.连接、、、.
∵,,
∴,
∴,
即,
设圆半径为r,设,,则,,
∴,,
∴,
解得:,
∵平分,,
∴.
在和中,设,,由勾股定理得:
,,
∴,
解得:,.
在中,,
∵,
∴,
∵,
∴,
∴;
(3)解:如图,连接,,,,
设,由(2)可得,,
则,
∴ ,
∴,
由(1)可得,
∴是等边三角形,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
又,
∴,
∴,
∴,
∴,
延长交于点,
则,,
则是等边三角形,
过点作于点, 于点,,交于点,连接,
∵是等边三角形,
∴,,
∵,,
∴是的重心,
∴,
在中,,,,
∴,
∴,
解得:,
∴.
22.解:(1)如图,过点A作于点H,
∵,,
∴,
∴.
∵是以为底边的等腰三角形,,
∴,.
∴.
∴.
∴.
∴.
∴.
∵,
∴.
∴.
∴.
∵,H为的中点,
∴.
在中,,
∴.
∴.
∴.
又,
∴;
(2)解:;
如图,过点A作于点H,
∵,,
∴,
∴.
∵是以为底边的等腰三角形,,
∴,.
∴.
∴.
∴.
∴.
∴.
∵,
∴.
∴.
∴.
∵,H为的中点,
∴.
在中,,
∴.
∴.
∴.
(3).
方法一:
如图,过点D作于点M,过点C作,交延长线于点H,
∴.
∴.
∵线段绕点D顺时针旋转得到线段,
∴.
∴.
∵是以为底边的等腰三角形,,
∴,.
∴.
∴.
∴.
∵,
∴.
设,则,
∵,
∴,
∴.
∴.
∵,
∴,.
∴.
在中,,,
∴.
∴,解得.
∴.
∵,
∴.
方法二:
如图,过点C作交延长线于点G,过点D作于点M,过点E作于点H,
∴.
∴.
∵线段绕点D顺时针旋转得到线段,
∴.
∴.
∵,
∴,.
∴.
∵,
∴.
∵是以为底边的等腰三角形,,
∴.
∵,
∴,.
∴.
设,则,
∵,
∴.
∴.
∴.
∴.
在中,,
∴.
在中,,,
∴.
∴,解得.
∴.
∵,
∴.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
