28.1 锐角三角函数 同步练习(含答案) 人教版数学九年级下册
文档属性
| 名称 | 28.1 锐角三角函数 同步练习(含答案) 人教版数学九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 198.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 11:42:42 | ||
图片预览


文档简介
28.1 锐角三角函数
一、单选题
1.已知在Rt△ABC中,∠C=90°,sinA= ,则tanB的值为( )
A. B. C. D.
2.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,BC=3,AC=4,则sin∠DCB的值为( )
A. B. C. D.
3.如图,在矩形ABCD中,以点A为圆心,AD的长为半径画弧,交AB于点E,取BC的中点F,过点F作一直线与AB平行,且交弧DE于点G,则∠AGF的度数为 ( )
A.110° B.120° C.135° D.150°
4.如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,,则“人字梯”的顶端离地面的高度AD是( )
A.144cm B.180cm C.240cm D.360cm
5.如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为( )
A. B.1 C. D.
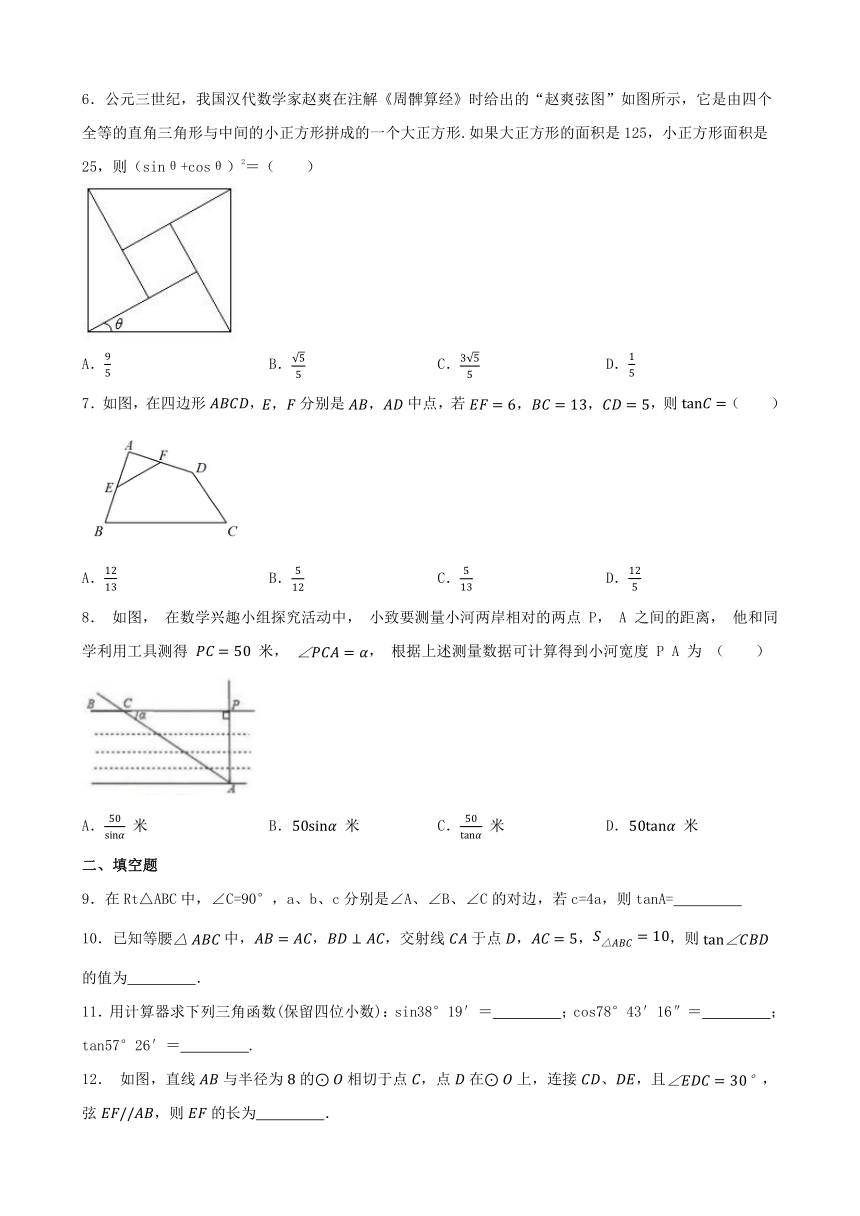
6.公元三世纪,我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是125,小正方形面积是25,则(sinθ+cosθ)2=( )
A. B. C. D.
7.如图,在四边形,分别是中点,若,则( )
A. B. C. D.
8. 如图, 在数学兴趣小组探究活动中, 小致要测量小河两岸相对的两点 P, A 之间的距离, 他和同学利用工具测得 米, , 根据上述测量数据可计算得到小河宽度 P A 为 ( )
A. 米 B. 米 C. 米 D. 米
二、填空题
9.在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,若c=4a,则tanA=
10.已知等腰中,,,交射线于点,,,则的值为 .
11.用计算器求下列三角函数(保留四位小数):sin38°19′= ;cos78°43′16″= ;tan57°26′= .
12. 如图,直线与半径为的相切于点,点在上,连接、,且,弦,则的长为 .
13.如图,已知点坐标为,为轴正半轴上一动点,则度数为 ,在点运动的过程中的最小值为 .
三、解答题
14.先化简,再求代数式 的值,其中a=tan60° .
15.如图,在 中, , , .求 , 和 .
16.超速行驶是引发交通事故的主要原因,上周末,小鹏等三位同学在滨海大道红树林路段,尝试用自己所学的知识检测车速,已知该路段最高时速不超过80千米,如图:观测点设在到公路l的距离为100米的P处,这时,一辆富康轿车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°,试计算AB的长度并判断此车是否超速?(参考数据: , )
17.如图,已知,是对角线上两点,.
(1)求证:;
(2)若交的延长线于点,,求的面积.
18.如图,AB是⊙O的直径,OC是半径,延长OC至点D.连接AD,AC,BC.使∠CAD=∠B.
(1)求证:AD是⊙O的切线;
(2)若AD=4,tan∠CAD= ,求BC的长.
答案
1.A
2.A
3.D
4.B
5.B
6.A
7.D
8.D
9.
10.或2
11.0.6193;0.1956;1.5657
12.
13.30°;
14.解:原式= ÷
=
= ,
当a=tan60°﹣ sin45°= ﹣1时,原式= =3﹣
15.解:在 中, , , ,
∴
∴ , , .
16.解:在 中, ,
在 中, ,
∴ ,
车速= ,没有超速.
17.(1)证明:∵,
∴,,
∴,
又∵,
∴;
(2)解:∵,
∴
又∵,,
∴,即:,
解得:(负值已舍去),
∴,
又∵,
∴,
∴,
∴平行四边形的面积,
18.(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠B+∠BAC=90°,
∵∠CAD=∠B,
∴∠CAD+∠BAC=90°,
即∠BAD=90°,
∴AD⊥OA,
∴AD是⊙O的切线;
(2)解:过点D作DM⊥AD交AC的延长线于点M,
∵tan∠CAD= = ,AD=4,
∴DM=2,
∵OA=OC,
∴∠OAC=∠OCA,
∵AD⊥OA,DM⊥AD,
∴OA∥DM,
∴∠M=∠OAC,
∵∠OCA=∠DCM,
∴∠DCM=∠M,
∴DC=DM=2,
在Rt△OAD中,OA2+AD2=OD2,
即OA2+42=(OC+2)2=(OA+2)2,
∴OA=3,
∴AB=6,
∵∠CAD=∠B,tan∠CAD= ,
∴tanB=tan∠CAD= = ,
∴BC=2AC,
在Rt△ABC中,AB2=AC2+BC2,
∴62=5AC2,
∴AC= ,
∴BC=
一、单选题
1.已知在Rt△ABC中,∠C=90°,sinA= ,则tanB的值为( )
A. B. C. D.
2.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,BC=3,AC=4,则sin∠DCB的值为( )
A. B. C. D.
3.如图,在矩形ABCD中,以点A为圆心,AD的长为半径画弧,交AB于点E,取BC的中点F,过点F作一直线与AB平行,且交弧DE于点G,则∠AGF的度数为 ( )
A.110° B.120° C.135° D.150°
4.如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,,则“人字梯”的顶端离地面的高度AD是( )
A.144cm B.180cm C.240cm D.360cm
5.如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为( )
A. B.1 C. D.
6.公元三世纪,我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是125,小正方形面积是25,则(sinθ+cosθ)2=( )
A. B. C. D.
7.如图,在四边形,分别是中点,若,则( )
A. B. C. D.
8. 如图, 在数学兴趣小组探究活动中, 小致要测量小河两岸相对的两点 P, A 之间的距离, 他和同学利用工具测得 米, , 根据上述测量数据可计算得到小河宽度 P A 为 ( )
A. 米 B. 米 C. 米 D. 米
二、填空题
9.在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,若c=4a,则tanA=
10.已知等腰中,,,交射线于点,,,则的值为 .
11.用计算器求下列三角函数(保留四位小数):sin38°19′= ;cos78°43′16″= ;tan57°26′= .
12. 如图,直线与半径为的相切于点,点在上,连接、,且,弦,则的长为 .
13.如图,已知点坐标为,为轴正半轴上一动点,则度数为 ,在点运动的过程中的最小值为 .
三、解答题
14.先化简,再求代数式 的值,其中a=tan60° .
15.如图,在 中, , , .求 , 和 .
16.超速行驶是引发交通事故的主要原因,上周末,小鹏等三位同学在滨海大道红树林路段,尝试用自己所学的知识检测车速,已知该路段最高时速不超过80千米,如图:观测点设在到公路l的距离为100米的P处,这时,一辆富康轿车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°,试计算AB的长度并判断此车是否超速?(参考数据: , )
17.如图,已知,是对角线上两点,.
(1)求证:;
(2)若交的延长线于点,,求的面积.
18.如图,AB是⊙O的直径,OC是半径,延长OC至点D.连接AD,AC,BC.使∠CAD=∠B.
(1)求证:AD是⊙O的切线;
(2)若AD=4,tan∠CAD= ,求BC的长.
答案
1.A
2.A
3.D
4.B
5.B
6.A
7.D
8.D
9.
10.或2
11.0.6193;0.1956;1.5657
12.
13.30°;
14.解:原式= ÷
=
= ,
当a=tan60°﹣ sin45°= ﹣1时,原式= =3﹣
15.解:在 中, , , ,
∴
∴ , , .
16.解:在 中, ,
在 中, ,
∴ ,
车速= ,没有超速.
17.(1)证明:∵,
∴,,
∴,
又∵,
∴;
(2)解:∵,
∴
又∵,,
∴,即:,
解得:(负值已舍去),
∴,
又∵,
∴,
∴,
∴平行四边形的面积,
18.(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠B+∠BAC=90°,
∵∠CAD=∠B,
∴∠CAD+∠BAC=90°,
即∠BAD=90°,
∴AD⊥OA,
∴AD是⊙O的切线;
(2)解:过点D作DM⊥AD交AC的延长线于点M,
∵tan∠CAD= = ,AD=4,
∴DM=2,
∵OA=OC,
∴∠OAC=∠OCA,
∵AD⊥OA,DM⊥AD,
∴OA∥DM,
∴∠M=∠OAC,
∵∠OCA=∠DCM,
∴∠DCM=∠M,
∴DC=DM=2,
在Rt△OAD中,OA2+AD2=OD2,
即OA2+42=(OC+2)2=(OA+2)2,
∴OA=3,
∴AB=6,
∵∠CAD=∠B,tan∠CAD= ,
∴tanB=tan∠CAD= = ,
∴BC=2AC,
在Rt△ABC中,AB2=AC2+BC2,
∴62=5AC2,
∴AC= ,
∴BC=
