北师大版数学九年级上册 第六章 反比例函数 单元测试 (含答案)
文档属性
| 名称 | 北师大版数学九年级上册 第六章 反比例函数 单元测试 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 144.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 12:23:44 | ||
图片预览


文档简介
第六章 反比例函数
一、单选题
1.反比例函数,下列说法错误的是( )
A.图象经过点(1,﹣1) B.图象位于第二、四象限
C.图象关于直线y=﹣x对称 D.y随x的增大而增大
2.若点A(a﹣1,y1),B(a+1,y2)在反比例函数的图象上,且y1>y2,则a的取值范围是( )
A.a<﹣1 B.﹣1<a<1
C.a>1 D.a<﹣1或a>1
3.方程x2+4x﹣1=0的根可视为函数y=x+4的图象与函数的图象交点的横坐标,那么用此方法可推断出:当m取任意正实数时,方程x3+mx﹣1=0的实根x0一定在( )范围内.
A.﹣1<x0<0 B.0<x0<1 C.1<x0<2 D.2<x0<3
4.一次函数y=ax+b与反比例函数y= 的图象如图所示,则( )
A.a>0,b>0.c>0 B.a<0,b<0.c<0
C.a<0,b>0.c>0 D.a<0,b<0.c>0
5.如图,反比例函数y=的图象与直线y=kx(k>0)相交于A、B两点,AC∥y轴,BC∥x轴,则△ABC的面积等于( )个面积单位.
A.4 B.5 C.10 D.20
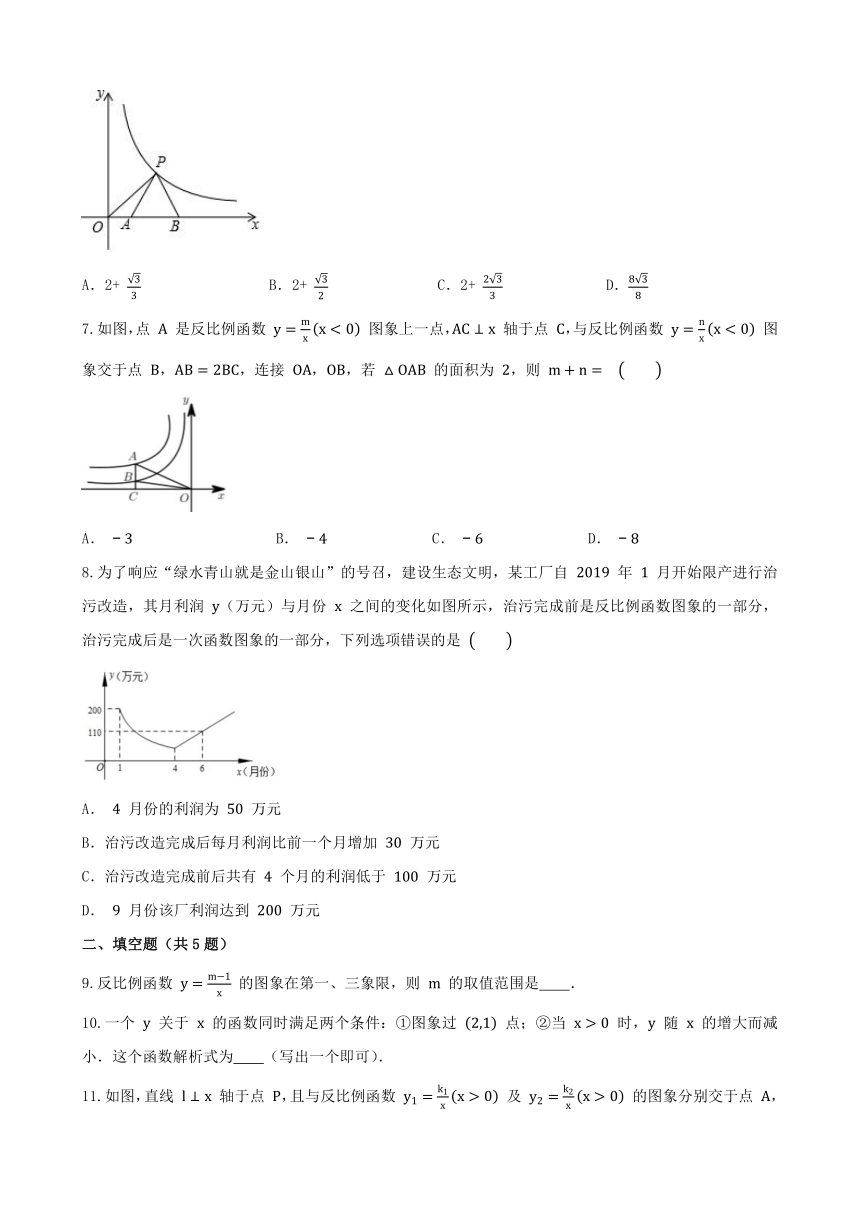
6.如图,P(m,m)是反比例函数y= 在第一象限内的图象上一点,以P为顶点作等边△PAB,使AB落在x轴上,则△POB的面积为( )
A.2+ B.2+ C.2+ D.
7.如图,点 是反比例函数 图象上一点, 轴于点 ,与反比例函数 图象交于点 ,,连接 ,,若 的面积为 ,则
A. B. C. D.
8.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自 年 月开始限产进行治污改造,其月利润 (万元)与月份 之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是
A. 月份的利润为 万元
B.治污改造完成后每月利润比前一个月增加 万元
C.治污改造完成前后共有 个月的利润低于 万元
D. 月份该厂利润达到 万元
二、填空题(共5题)
9.反比例函数 的图象在第一、三象限,则 的取值范围是 .
10.一个 关于 的函数同时满足两个条件:①图象过 点;②当 时, 随 的增大而减小.这个函数解析式为 (写出一个即可).
11.如图,直线 轴于点 ,且与反比例函数 及 的图象分别交于点 ,,连接 ,,已知 的面积为 ,则 .
12.如图,在平面直角坐标系中,函数 的图象与等边三角形 的边 , 分别交于点 ,,且 ,若 ,那么点 的横坐标为 .
13.如图,直线AB与双曲线y= (k<0)交于点A,B,点P是直线AB上一动点,且点P在第二象限.连接PO并延长交双曲线于点C.过点P作PD⊥y轴,垂足为点D.过点C作CE⊥x轴,垂足为E.若点A的坐标为(﹣2,3),点B的坐标为(m,1),设△POD的面积为S1,△COE的面积为S2,当S1>S2时,点P的横坐标x的取值范围为 .
三、解答题
14.反比例函数y=(m-2)x2m+1的函数值为3时,求自变量x的值.
15.已知直线y=k1x+b与双曲线y=相交于点A(2,4),且与x轴、y轴分别交于B、C两点,AD垂直平分OB,垂足为D,求直线和双曲线的解析式
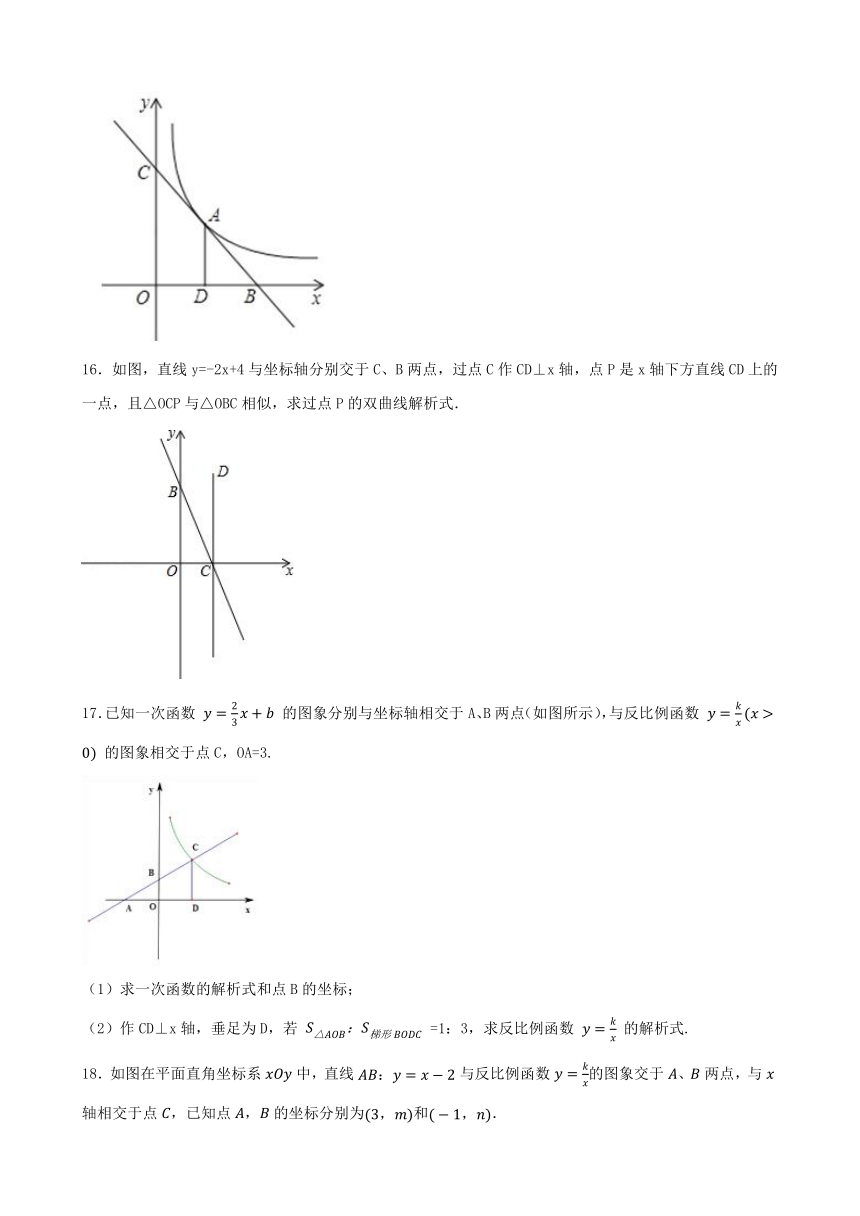
16.如图,直线y=-2x+4与坐标轴分别交于C、B两点,过点C作CD⊥x轴,点P是x轴下方直线CD上的一点,且△OCP与△OBC相似,求过点P的双曲线解析式.
17.已知一次函数 的图象分别与坐标轴相交于A、B两点(如图所示),与反比例函数 的图象相交于点C,OA=3.
(1)求一次函数的解析式和点B的坐标;
(2)作CD⊥x轴,垂足为D,若 =1:3,求反比例函数 的解析式.
18.如图在平面直角坐标系中,直线与反比例函数的图象交于、两点,与轴相交于点,已知点,的坐标分别为和.
(1)求反比例函数的解析式;
(2)请直接写出不等式的解集;
(3)点为反比例函数图象的任意一点,若,求点的坐标.
参考答案
1.D
2.D
3.B
4.B
5.C
6.C
7. D
8. C
9.
10. (答案不唯一)
11.
12.
13.﹣6<x<﹣2
14.解答: 由反比例函数y=(m-2)x2m+1,得2m+1=-1.解得m-1,由比例函数y=-3x-1的函数值为3,得-3x-1=3.解得x=-1
15.解:∵双曲线y=经过点A(2,4)
∴k2=8,
∴双曲线的解析式为y=,
∵A(2,4),AD⊥OB,AD平分OB,
∴OB=4,B(4,0),
∵直线y=k1x+b经过点A(2,4),B(4,0)
∴
解得
∴直线的解析式为y=﹣2x+8,
16.解:∵直线y=-2x+4与坐标轴分别交于C、B两点,
∴令y=0,可得-2x+4=0,解得x=2,即C(2,0),OC=2,
令x=0,可得y=4,即B(0,4),OB=4,
①如图1,当∠OBC=∠COP时,△OCP与△OBC相似,
∴ ,即 ,解得CP=1,
∴P(2,-1),
设过点P的双曲线解析式y= ,把P点代入得-1= ,解得k=-2,
∴过点P的双曲线解析式 ,
②如图2,当∠OBC=∠CPO时,△OCP与△OBC相似,
在△OCP和△COB中,
∴△OCP≌△COB(AAS)
∴CP=BO=4,
∴P(2,-4)
设过点P的双曲线解析式y= ,把P点代入得-4= ,解得k=-8,
∴过点P的双曲线解析式 .
综上所述,过点P的双曲线解析式为: 或 .
17.(1)解:∵OA=3
∴A(-3,0)
将A(-3,0)代入 中得b=2
∴一次函数的解析式为
令x=0得y=2
∴点B的坐标为(0,2)
(2)解:由题知
∵ =1:3
∴ =9
设C(m, ),则有
解得m1=3,m2=-9(舍去)
∴C(3,4)
∵C(3,4)在反比例函数 上
∴反比例函数的解析式为 .
18.(1)解:把点代入直线得:
∴点A的坐标为:,
∵反比例函数的图象过点A,
∴,
即反比例函数的解析式为,
(2)解:由(1)得:点A的坐标为:,
同理可求,点B的坐标为:,
∴不等式的解集为或;
(3)解:把代入得:,
即点C的坐标为:,
∴,
∵,
∴,
∴,
当点P的纵坐标为3时,则,解得,
当点P的纵坐标为时,则,解得,
∴点P的坐标为或
一、单选题
1.反比例函数,下列说法错误的是( )
A.图象经过点(1,﹣1) B.图象位于第二、四象限
C.图象关于直线y=﹣x对称 D.y随x的增大而增大
2.若点A(a﹣1,y1),B(a+1,y2)在反比例函数的图象上,且y1>y2,则a的取值范围是( )
A.a<﹣1 B.﹣1<a<1
C.a>1 D.a<﹣1或a>1
3.方程x2+4x﹣1=0的根可视为函数y=x+4的图象与函数的图象交点的横坐标,那么用此方法可推断出:当m取任意正实数时,方程x3+mx﹣1=0的实根x0一定在( )范围内.
A.﹣1<x0<0 B.0<x0<1 C.1<x0<2 D.2<x0<3
4.一次函数y=ax+b与反比例函数y= 的图象如图所示,则( )
A.a>0,b>0.c>0 B.a<0,b<0.c<0
C.a<0,b>0.c>0 D.a<0,b<0.c>0
5.如图,反比例函数y=的图象与直线y=kx(k>0)相交于A、B两点,AC∥y轴,BC∥x轴,则△ABC的面积等于( )个面积单位.
A.4 B.5 C.10 D.20
6.如图,P(m,m)是反比例函数y= 在第一象限内的图象上一点,以P为顶点作等边△PAB,使AB落在x轴上,则△POB的面积为( )
A.2+ B.2+ C.2+ D.
7.如图,点 是反比例函数 图象上一点, 轴于点 ,与反比例函数 图象交于点 ,,连接 ,,若 的面积为 ,则
A. B. C. D.
8.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自 年 月开始限产进行治污改造,其月利润 (万元)与月份 之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是
A. 月份的利润为 万元
B.治污改造完成后每月利润比前一个月增加 万元
C.治污改造完成前后共有 个月的利润低于 万元
D. 月份该厂利润达到 万元
二、填空题(共5题)
9.反比例函数 的图象在第一、三象限,则 的取值范围是 .
10.一个 关于 的函数同时满足两个条件:①图象过 点;②当 时, 随 的增大而减小.这个函数解析式为 (写出一个即可).
11.如图,直线 轴于点 ,且与反比例函数 及 的图象分别交于点 ,,连接 ,,已知 的面积为 ,则 .
12.如图,在平面直角坐标系中,函数 的图象与等边三角形 的边 , 分别交于点 ,,且 ,若 ,那么点 的横坐标为 .
13.如图,直线AB与双曲线y= (k<0)交于点A,B,点P是直线AB上一动点,且点P在第二象限.连接PO并延长交双曲线于点C.过点P作PD⊥y轴,垂足为点D.过点C作CE⊥x轴,垂足为E.若点A的坐标为(﹣2,3),点B的坐标为(m,1),设△POD的面积为S1,△COE的面积为S2,当S1>S2时,点P的横坐标x的取值范围为 .
三、解答题
14.反比例函数y=(m-2)x2m+1的函数值为3时,求自变量x的值.
15.已知直线y=k1x+b与双曲线y=相交于点A(2,4),且与x轴、y轴分别交于B、C两点,AD垂直平分OB,垂足为D,求直线和双曲线的解析式
16.如图,直线y=-2x+4与坐标轴分别交于C、B两点,过点C作CD⊥x轴,点P是x轴下方直线CD上的一点,且△OCP与△OBC相似,求过点P的双曲线解析式.
17.已知一次函数 的图象分别与坐标轴相交于A、B两点(如图所示),与反比例函数 的图象相交于点C,OA=3.
(1)求一次函数的解析式和点B的坐标;
(2)作CD⊥x轴,垂足为D,若 =1:3,求反比例函数 的解析式.
18.如图在平面直角坐标系中,直线与反比例函数的图象交于、两点,与轴相交于点,已知点,的坐标分别为和.
(1)求反比例函数的解析式;
(2)请直接写出不等式的解集;
(3)点为反比例函数图象的任意一点,若,求点的坐标.
参考答案
1.D
2.D
3.B
4.B
5.C
6.C
7. D
8. C
9.
10. (答案不唯一)
11.
12.
13.﹣6<x<﹣2
14.解答: 由反比例函数y=(m-2)x2m+1,得2m+1=-1.解得m-1,由比例函数y=-3x-1的函数值为3,得-3x-1=3.解得x=-1
15.解:∵双曲线y=经过点A(2,4)
∴k2=8,
∴双曲线的解析式为y=,
∵A(2,4),AD⊥OB,AD平分OB,
∴OB=4,B(4,0),
∵直线y=k1x+b经过点A(2,4),B(4,0)
∴
解得
∴直线的解析式为y=﹣2x+8,
16.解:∵直线y=-2x+4与坐标轴分别交于C、B两点,
∴令y=0,可得-2x+4=0,解得x=2,即C(2,0),OC=2,
令x=0,可得y=4,即B(0,4),OB=4,
①如图1,当∠OBC=∠COP时,△OCP与△OBC相似,
∴ ,即 ,解得CP=1,
∴P(2,-1),
设过点P的双曲线解析式y= ,把P点代入得-1= ,解得k=-2,
∴过点P的双曲线解析式 ,
②如图2,当∠OBC=∠CPO时,△OCP与△OBC相似,
在△OCP和△COB中,
∴△OCP≌△COB(AAS)
∴CP=BO=4,
∴P(2,-4)
设过点P的双曲线解析式y= ,把P点代入得-4= ,解得k=-8,
∴过点P的双曲线解析式 .
综上所述,过点P的双曲线解析式为: 或 .
17.(1)解:∵OA=3
∴A(-3,0)
将A(-3,0)代入 中得b=2
∴一次函数的解析式为
令x=0得y=2
∴点B的坐标为(0,2)
(2)解:由题知
∵ =1:3
∴ =9
设C(m, ),则有
解得m1=3,m2=-9(舍去)
∴C(3,4)
∵C(3,4)在反比例函数 上
∴反比例函数的解析式为 .
18.(1)解:把点代入直线得:
∴点A的坐标为:,
∵反比例函数的图象过点A,
∴,
即反比例函数的解析式为,
(2)解:由(1)得:点A的坐标为:,
同理可求,点B的坐标为:,
∴不等式的解集为或;
(3)解:把代入得:,
即点C的坐标为:,
∴,
∵,
∴,
∴,
当点P的纵坐标为3时,则,解得,
当点P的纵坐标为时,则,解得,
∴点P的坐标为或
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
