用字母表示数应用题易错大集结-数学五年级上册苏教版(含解析)
文档属性
| 名称 | 用字母表示数应用题易错大集结-数学五年级上册苏教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 15:49:45 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
用字母表示数应用题易错大集结-数学五年级上册苏教版
1.铺设一条长4000米的自来水管道,已经铺了6天,每天铺a米。
(1)用含有字母的式子表示没有铺的米数。
(2)当a=500米时,还剩多少米没铺?
2.某商店一天上午卖出23个花瓶,下午又卖出49个同样的花瓶,若每个花瓶x元。
(1)这天卖花瓶的收入一共是多少元?
(2)如果每个花瓶12.5元,这天卖花瓶的收入一共是多少元?
3.小明每分钟走70米,小丽每分钟走58米。
(1)小明和小丽同时从家出发向学校走去,经过a分钟在学校相遇。小明家和小丽家相距( )米。
(2)当a=5米时,小明和小丽家相距多少米?
(3)如果两人同时从学校出发向少年宫走去,当小明到达少年宫时,小丽离少年宫还有多少米?
4.一把椅子x元,一张桌子的价钱比一把椅子价钱的3倍少20元。
(1)用含有字母的式子表示一张桌子比一把椅子贵多少元?
(2)当x=50时,一张桌子比一把椅子贵多少元?
5.下图中正方形的边长是a厘米,长方形的长是a厘米,宽是b厘米。
(1)用含有字母的式子表示图中涂色部分面积。
(2)当a=12,b=6时,涂色部分的面积是多少平方厘米?
6.观察下图阴影方框内中间的数与其他四个数的关系。
(1)中间的数用表示,左边的数是( ),下面的数是( ),方框中5个数的和是( )。
(2)当5个数的和是110时,这5个数分别是多少?在下图方格中填一填。
7.学校买来9个足球,单价是a元/个;又买来b个篮球,单价是21.5元/个。
(1)用含有字母的式子表示买足球和篮球一共用去了多少元?
(2)当a=28,b=10时,买足球比篮球多用去了多少元?
8.幼儿园教师把一箱饼干分给小班和中班的小朋友,平均每人分得6块;如果只分给中班的小朋友,平均每人可以多分得4块,如果只分给小班的小朋友,平均每人分得多少块?
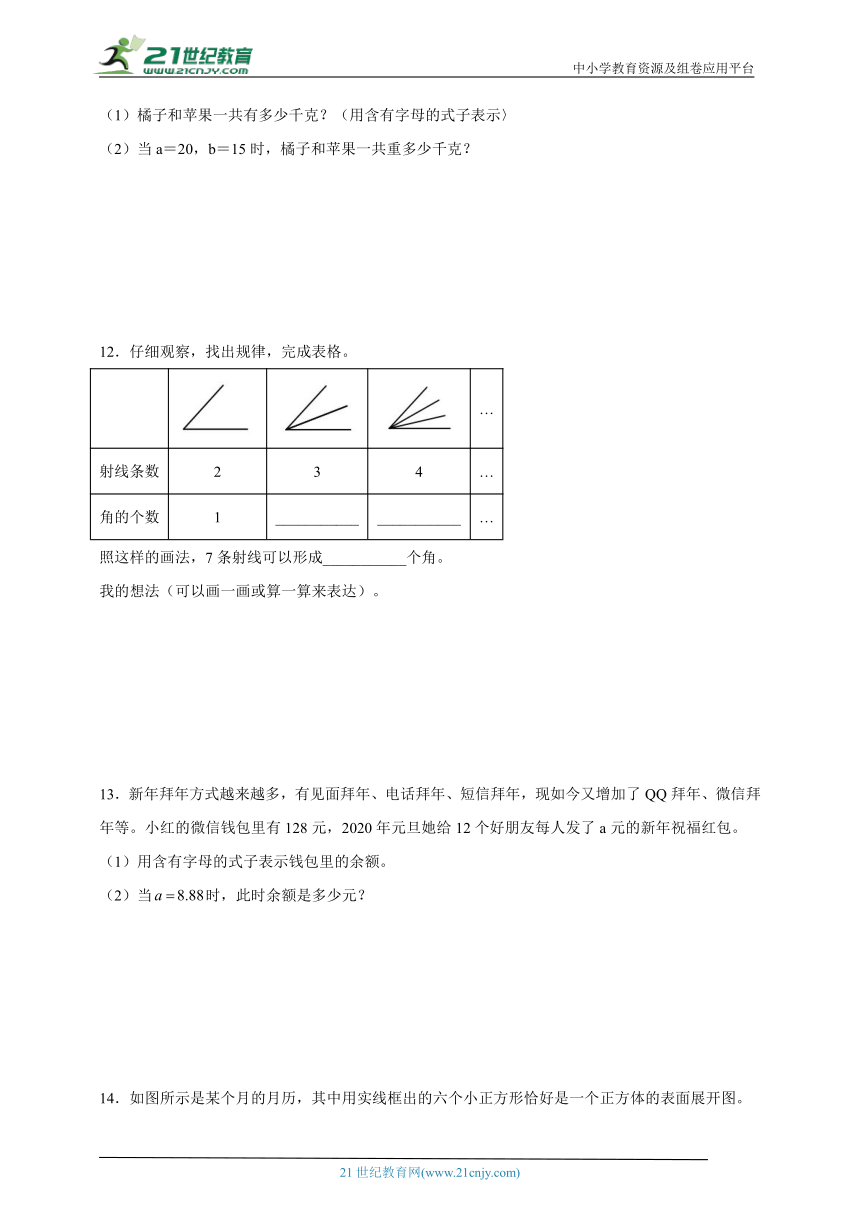
9.如图是学校科学实验室和实验准备室的平面图。
(1)用含有字母的式子表示科学实验室和实验准备室的总面积。
(2)当b=8.5时,求科学实验室和实验准备室的总面积。
10.把2个长5厘米,宽a厘米的小长方形拼成一个大长方形。
(1)用含有字母的式子表示这个大长方形的面积是多少?
(2)当a=2.6时,这个大长方形的周长可能是多少?
11.水果店运来10筐苹果,8筐橘子。每筐苹果a千克,每筐橘子b千克。
(1)橘子和苹果一共有多少千克?(用含有字母的式子表示〉
(2)当a=20,b=15时,橘子和苹果一共重多少千克?
12.仔细观察,找出规律,完成表格。
…
射线条数 2 3 4 …
角的个数 1 ___________ ___________ …
照这样的画法,7条射线可以形成___________个角。
我的想法(可以画一画或算一算来表达)。
13.新年拜年方式越来越多,有见面拜年、电话拜年、短信拜年,现如今又增加了QQ拜年、微信拜年等。小红的微信钱包里有128元,2020年元旦她给12个好朋友每人发了a元的新年祝福红包。
(1)用含有字母的式子表示钱包里的余额。
(2)当时,此时余额是多少元?
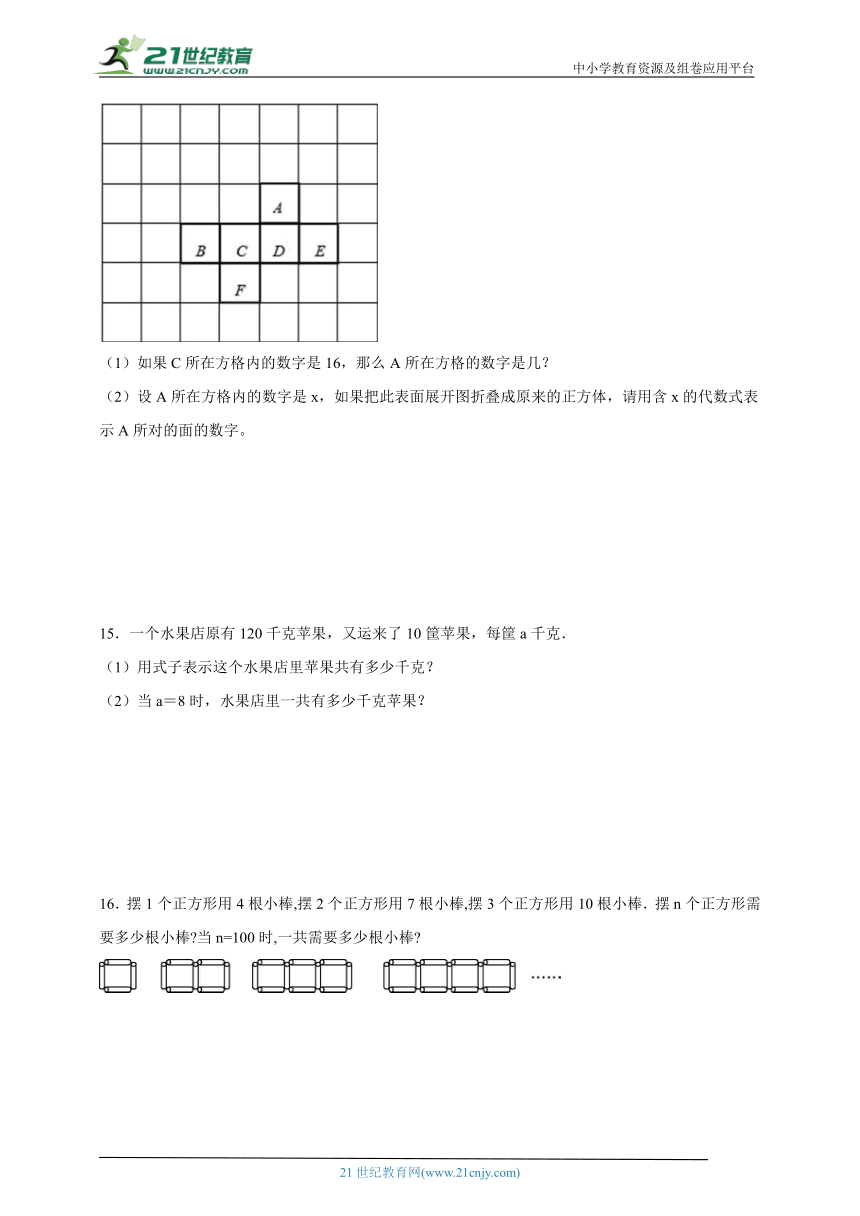
14.如图所示是某个月的月历,其中用实线框出的六个小正方形恰好是一个正方体的表面展开图。
(1)如果C所在方格内的数字是16,那么A所在方格的数字是几?
(2)设A所在方格内的数字是x,如果把此表面展开图折叠成原来的正方体,请用含x的代数式表示A所对的面的数字。
15.一个水果店原有120千克苹果,又运来了10筐苹果,每筐a千克.
(1)用式子表示这个水果店里苹果共有多少千克?
(2)当a=8时,水果店里一共有多少千克苹果?
16.摆1个正方形用4根小棒,摆2个正方形用7根小棒,摆3个正方形用10根小棒.摆n个正方形需要多少根小棒 当n=100时,一共需要多少根小棒
17.明明到商店买东西.
(1)买a盒牛奶应付多少元
品名 单价 数量
牛奶 2元/盒 a盒
(2)如果明明付给售货员100元,用含有字母的式子表示应找回多少元.当a=5时,应找回多少元
18.梦想剧场楼上有A排,每排30个座位;楼下有B排,每排38个座位.
(1)用式子表示这个剧场共有多少座位.
(2)当A=15时,B=20时,求这个剧场一共有多少个座位?
19.一根弹簧原来的长度是10厘米,当弹簧受到拉力F(F在一定范围内)时,弹簧的长度用L表示,测得有关数据如下表:
拉力F(千克) 弹簧的长度L(厘米)
1 10+0.5
2 10+1
3 10+1.5
4 10+2
…… ……
思考:
(1)写出当F=7时,弹簧的长度L为多少厘米
(2)写出弹簧的长度L与拉力F的关系式.
(3)计算当拉力F=100时,弹簧的长度L为多少厘米
20.一台碾米机上午碾米2小时,下午碾米5小时,已知每小时碾米x千克。
(1)用含有字母的式子表示这一天一共碾米的质量和上午比下午少碾米的质量。
(2)当x=200时,这一天一共碾米多少千克?上午比下午少碾米多少千克?
参考答案:
1.(1)(4000-6a)米;
(2)1000米
【分析】(1)用每天铺的米数×铺的天数,求出已经铺的长度,再用总长度-已经铺的长度就是没有铺的米数;
(2)将a=500,带入(1)中求值即可。
【详解】(1)4000-6×a=(4000-6a)(米)
答:没有铺的是(4000-6a)米。
(2)当a=500时,4000-6a=4000-6×500=1000
答:当a=500米时,还剩1000米没铺。
【点睛】本题主要考查用字母表示数及求含有字母式子的值。
2.(1)72x元
(2)900元
【分析】(1)上午卖出23个花瓶,下午又卖出49个同样的花瓶,一天共卖花瓶23+49=72个,若每个花瓶x元,根据总价、单价和数量的关系,这天卖花瓶的收入是72x元。
(2)将x=12.5代入式子72x求值即可。
【详解】(1)若每个花瓶x元,这天的收入:
(23+49)×x
=72×x
=72x(元)
答:这天卖花瓶的收入一共是72x元。
(2)将x=12.5代入式子72x得:72×12.5=900(元)
答:如果每个花瓶12.5元,这天卖花瓶的收入一共是900元。
【点睛】本题主要考查了对单价×数量=总价的理解和灵活运用情况,数字与字母相乘,可以省略乘号,数字写在字母的前面。
3.(1)128a
(2)640米
(3)84米
【分析】(1)速度和×相遇时间=总路程,据此解答。
(2)把a=5代入(1)题的结果进行计算即可。
(3)学校到少年宫490米,用490除以小明的速度求出他到达少年宫所用的时间,再用这个时间乘小丽的速度求出小丽已经走的路程,最后用总路程减去已经走的路程即可求出小丽离少年宫还有多少米。
【详解】(1)(70+58)a=128a(米)
(2)把a=5代入128a,则
128a=128×5
=640
答:小明和小丽家相距640米。
(3)490÷70=7(分)
490-58×7
=490-406
=84(米)
答:小丽离少年宫还有84米。
【点睛】根据“速度和×相遇时间=总路程”即可用含有字母的式子表示小明家和小丽家的距离;明确小明到达少年宫所用的时间就是小丽这时所用的时间是解题的关键。
4.(1)(2x-20)元
(2)80元
【分析】(1)由题意可知:一张桌子的价钱=一把椅子价钱×3-20元,代入未知数表示出桌子的价钱,再求差即可;
(2)将x=50代入(1)中求值即可。
【详解】(1)3×x-20-x=2x-20
答:一张桌子比一把椅子贵2x-20元。
(2)当x=50时,2x-20=2×50-20=80(元)
答:当x=50时,一张桌子比一把椅子贵80元。
【点睛】本题主要考查含有字母式子的化简与求值。
5.(1)a2+ab平方厘米;(2)216平方厘米
【分析】(1)正方形的面积=边长×边长;长方形的面积=长×宽,据此计算正方形和长方形的面积,再相加;
(2)把数据代入到含有字母的式子中,计算即可。
【详解】(1)涂色部分的面积是:a2+ab平方厘米;
(2)当a=12,b=6时,
a2+ab
=12×12+12×6
=144+72
=216(平方厘米)
【点睛】此题考查的是用字母表示数的意义以及求含有字母的式子的值。
6.(1)y-1;y+7;5y
(2)21;22;23;15;29;图见详解
【分析】(1)观察表格中数与数之间的规律可以发现,上下两个相邻数之间相差7,左右两个相邻数之间相差1,据此写出左边数和下边数,求出5个数的和;
(2)根据表格中数与数之间的规律,求出中间数,再根据规律,求出这5个数,再填上方格。
【详解】(1)左边数:y-1,下面数:y+7
(y-1)+y+(y+1)+(y-7)+(y+7)
=y-1+y+y+1+y-7+y+7
=5y
(2)中间数:110÷5=22
左边:22-1=21
右边:22+1=23
上面:22-7=15
下面:22+7=29
【点睛】解答本题的关键是找出表格中的规律,进而求出问题。
7.(1)(9a+21.5b)元;
(2)37元
【分析】(1)总价=单价×数量,再相加即可求出买足球和篮球一共用去了多少元;
(2)当a=60,b=10时,买足球比篮球多用的钱数,用足球的总价减去篮球的总价,即:9a-21.5b,代入式子即可。
【详解】(1)9×a+21.5×b=(9a+21.5b)元
答:买足球和篮球一共用去了(9a+21.5b)元。
(2)当a=28,b=10时,
9a-21.5b
=9×28-21.5×10
=252-215
=37(元)
答:买足球比篮球多用去了37元。
【点睛】解答此题的关键是掌握总价=单价×数量这个公式。
8.15块
【分析】用字母a表示出小班和中班的小朋友人数,则饼干的总块数为6a,如果只分给中班的小朋友,平均每人分得(6+4)块,用除法算式表示出中班小朋友的人数,
小班小朋友的人数=总人数-中班小朋友的人数,小班小朋友每人分得的块数=饼干的总块数÷小班小朋友的人数,据此解答。
【详解】假设小班和中班的小朋友一共有a人,则饼干共6a块
中班小朋友人数:6a÷(6+4)=6a÷10=0.6a(人)
小班小朋友人数:a-0.6a=0.4a(人)
(6a)÷(0.4a)=15(块)
答:如果只分给小班的小朋友,平均每人分得15块。
【点睛】掌握含有字母的式子化简的方法是解答题目的关键。
9.(1)18b平方米
(2)153平方米
【分析】(1)依据长方形的面积公式:S=ab即可求出科学实验室和实验准备室的总面积;
(2)将b=8.5,代入问题(1)中的字母式子里面,即可得解。
【详解】(1)14b+4b=18b(平方米)
答:科学实验室和实验准备室的总面积是18b平方米。
(2)当b=8.5时,18b=18×8.5=153(平方米)
答:当b=8.5时,科学实验室和实验准备室的总面积是153平方米。
【点睛】本题考查用字母表示式子,解题关键是根据已知条件,把未知的数用字母表示出来,然后根据题意列式计算即可。
10.(1)10a;(2)25.2cm或20.4cm
【分析】(1)拼成的大长方形的长是10厘米,宽是a厘米,或者长是5厘米,宽是2a厘米。据此求出这个长方形的面积即可;
(2)根据(1)的分析,将a=2.6分别代入两种情况之中,求出这个长方形的周长。
【详解】(1)2×5×a=10a(平方厘米)
答:这个长方形的面积是10a平方厘米。
(2)①5×2×2+2.6×2
=20+5.2
=25.2(厘米)
②5×2+2.6×2×2
=10+10.4
=20.4(厘米)
答:这个大长方形的周长可能是25.2厘米或者20.4厘米。
【点睛】本题考查了含有字母式子的化简和求值,灵活运用长方形的面积和周长公式是解题的关键。
11.(1)(10a+8b)千克;
(2)320千克
【分析】(1)根据公式:筐数×重量=总重量,把数和字母代入公式即可求出苹果和橘子各多重,之后把苹果和橘子的重量相加即可。
(2)当a=20,b=15时,把a和b的值代入第一问求的式子,算出结果即可。
【详解】(1)苹果重量:10×a=10a(千克)
橘子重量:8×b=8b(千克)
共重:(10a+8b)千克。
答:橘子和苹果一共有:(10a+8b)千克。
(2)当a=20,b=15时
10×20+8×15
=200+120
=320(千克)
答:橘子和苹果一共重320千克。
【点睛】本题主要考查用字母表示数,把给出的字母当做已知数,再根据基本的数量关系解决问题即可,数字和字母之间的乘号可以省略,数字在前,字母在后。
12.3;6
21
过程见详解
【分析】通过数一数可知,当有3条射线时,角的个数有3个;当有4条射线时,角的个数有6个;当有5条射线时,角的个数有10个。由此我可以得出规律:条射线就有角:。
【详解】2条射线有角:(个);
3条射线有角:(个);
4条射线有角:(个);
…
射线条数 2 3 4 …
角的个数 1 3 6 …
所以条射线就有角:。
所以当时,可以形成角:(个)角。
【点睛】本题主要考查数与形的规律,解题时要结合题干,仔细分析,找到变化的规律,再利用规律解题。
13.(1)128-12a;(2)21.44元
【分析】(1)钱包里的余额=微信钱包原有的钱数-发给好朋友的钱数,发给好朋友的钱数=好朋友人数×每人发的钱数。
(2)当时,代入计算即可。
【详解】(1)钱包里的余额:128-12a
(2)当时
128-12a
=128-12×8.88
=128-106.56
=21.44(元)
答:此时余额是21.44元。
【点睛】此题主要考查用字母表示数以及含有字母的式子求值,解答时,把字母当做数,根据数量关系列式即可。
14.(1)10
(2)x+13
【分析】(1)根据题意可知:该图所示是某个月的月历,如果C所在方格内的数字是16,由此向前即可推出A所在的方格的数字是10;
(2)把展开图复原成正方体,则A所对的面是F,然后根据F代表的数字比A代表的数字多(23-10)=13;解答即可。
【详解】如图可知:
(1)A所在的方格的数字是10;
答:A所在方格的数字是10;
(2)把展开图复原成正方体,则A所对的面是F;如果A所在的方格数字是x,则:那么F所在的方格就是x+13;
即:A所对的面的数字是x+13。
【点睛】此题考查了简单图形覆盖现象中的规律,应根据月历中数的排列规律并结合正方体的特征进行解答。
15.(1) (120+10a)千克
(2) 200千克
【详解】(1)120+10a(千克);
答:这个水果店里苹果共有120+10a千克;
(2)当a=8时,代入120+10a,
120+10×8
=120+80
=200(千克);
答:商店一共有200千克苹果.
16.3n+1;301根
【详解】3n+1
当n=100时,3n+1=3×100+1=301.
17.(1)2a
(2)100-2a;90元
【详解】(1)2a
(2)当a=5时,100-2a=100-2×5=90.
18.(1)(30A+38B)个 (2)1210个
【详解】(1)楼上的座位有:30×A=30A(个)
楼下有座位:38×B=38B(个)
剧场共有(30A+38B)个座位.
(2)当A=15时,B=20时,
30A+38B=1210(个)
答:该剧场一共有1210个座位.
19.(1)10+7×0.5=13.5(厘米)
(2)L=10+0.5F
(3)L=10+0.5×100=60(厘米)
【详解】略
20.(1)2x+5x=7x,5x-2x=3x
(2)1400千克,600千克
【详解】略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
用字母表示数应用题易错大集结-数学五年级上册苏教版
1.铺设一条长4000米的自来水管道,已经铺了6天,每天铺a米。
(1)用含有字母的式子表示没有铺的米数。
(2)当a=500米时,还剩多少米没铺?
2.某商店一天上午卖出23个花瓶,下午又卖出49个同样的花瓶,若每个花瓶x元。
(1)这天卖花瓶的收入一共是多少元?
(2)如果每个花瓶12.5元,这天卖花瓶的收入一共是多少元?
3.小明每分钟走70米,小丽每分钟走58米。
(1)小明和小丽同时从家出发向学校走去,经过a分钟在学校相遇。小明家和小丽家相距( )米。
(2)当a=5米时,小明和小丽家相距多少米?
(3)如果两人同时从学校出发向少年宫走去,当小明到达少年宫时,小丽离少年宫还有多少米?
4.一把椅子x元,一张桌子的价钱比一把椅子价钱的3倍少20元。
(1)用含有字母的式子表示一张桌子比一把椅子贵多少元?
(2)当x=50时,一张桌子比一把椅子贵多少元?
5.下图中正方形的边长是a厘米,长方形的长是a厘米,宽是b厘米。
(1)用含有字母的式子表示图中涂色部分面积。
(2)当a=12,b=6时,涂色部分的面积是多少平方厘米?
6.观察下图阴影方框内中间的数与其他四个数的关系。
(1)中间的数用表示,左边的数是( ),下面的数是( ),方框中5个数的和是( )。
(2)当5个数的和是110时,这5个数分别是多少?在下图方格中填一填。
7.学校买来9个足球,单价是a元/个;又买来b个篮球,单价是21.5元/个。
(1)用含有字母的式子表示买足球和篮球一共用去了多少元?
(2)当a=28,b=10时,买足球比篮球多用去了多少元?
8.幼儿园教师把一箱饼干分给小班和中班的小朋友,平均每人分得6块;如果只分给中班的小朋友,平均每人可以多分得4块,如果只分给小班的小朋友,平均每人分得多少块?
9.如图是学校科学实验室和实验准备室的平面图。
(1)用含有字母的式子表示科学实验室和实验准备室的总面积。
(2)当b=8.5时,求科学实验室和实验准备室的总面积。
10.把2个长5厘米,宽a厘米的小长方形拼成一个大长方形。
(1)用含有字母的式子表示这个大长方形的面积是多少?
(2)当a=2.6时,这个大长方形的周长可能是多少?
11.水果店运来10筐苹果,8筐橘子。每筐苹果a千克,每筐橘子b千克。
(1)橘子和苹果一共有多少千克?(用含有字母的式子表示〉
(2)当a=20,b=15时,橘子和苹果一共重多少千克?
12.仔细观察,找出规律,完成表格。
…
射线条数 2 3 4 …
角的个数 1 ___________ ___________ …
照这样的画法,7条射线可以形成___________个角。
我的想法(可以画一画或算一算来表达)。
13.新年拜年方式越来越多,有见面拜年、电话拜年、短信拜年,现如今又增加了QQ拜年、微信拜年等。小红的微信钱包里有128元,2020年元旦她给12个好朋友每人发了a元的新年祝福红包。
(1)用含有字母的式子表示钱包里的余额。
(2)当时,此时余额是多少元?
14.如图所示是某个月的月历,其中用实线框出的六个小正方形恰好是一个正方体的表面展开图。
(1)如果C所在方格内的数字是16,那么A所在方格的数字是几?
(2)设A所在方格内的数字是x,如果把此表面展开图折叠成原来的正方体,请用含x的代数式表示A所对的面的数字。
15.一个水果店原有120千克苹果,又运来了10筐苹果,每筐a千克.
(1)用式子表示这个水果店里苹果共有多少千克?
(2)当a=8时,水果店里一共有多少千克苹果?
16.摆1个正方形用4根小棒,摆2个正方形用7根小棒,摆3个正方形用10根小棒.摆n个正方形需要多少根小棒 当n=100时,一共需要多少根小棒
17.明明到商店买东西.
(1)买a盒牛奶应付多少元
品名 单价 数量
牛奶 2元/盒 a盒
(2)如果明明付给售货员100元,用含有字母的式子表示应找回多少元.当a=5时,应找回多少元
18.梦想剧场楼上有A排,每排30个座位;楼下有B排,每排38个座位.
(1)用式子表示这个剧场共有多少座位.
(2)当A=15时,B=20时,求这个剧场一共有多少个座位?
19.一根弹簧原来的长度是10厘米,当弹簧受到拉力F(F在一定范围内)时,弹簧的长度用L表示,测得有关数据如下表:
拉力F(千克) 弹簧的长度L(厘米)
1 10+0.5
2 10+1
3 10+1.5
4 10+2
…… ……
思考:
(1)写出当F=7时,弹簧的长度L为多少厘米
(2)写出弹簧的长度L与拉力F的关系式.
(3)计算当拉力F=100时,弹簧的长度L为多少厘米
20.一台碾米机上午碾米2小时,下午碾米5小时,已知每小时碾米x千克。
(1)用含有字母的式子表示这一天一共碾米的质量和上午比下午少碾米的质量。
(2)当x=200时,这一天一共碾米多少千克?上午比下午少碾米多少千克?
参考答案:
1.(1)(4000-6a)米;
(2)1000米
【分析】(1)用每天铺的米数×铺的天数,求出已经铺的长度,再用总长度-已经铺的长度就是没有铺的米数;
(2)将a=500,带入(1)中求值即可。
【详解】(1)4000-6×a=(4000-6a)(米)
答:没有铺的是(4000-6a)米。
(2)当a=500时,4000-6a=4000-6×500=1000
答:当a=500米时,还剩1000米没铺。
【点睛】本题主要考查用字母表示数及求含有字母式子的值。
2.(1)72x元
(2)900元
【分析】(1)上午卖出23个花瓶,下午又卖出49个同样的花瓶,一天共卖花瓶23+49=72个,若每个花瓶x元,根据总价、单价和数量的关系,这天卖花瓶的收入是72x元。
(2)将x=12.5代入式子72x求值即可。
【详解】(1)若每个花瓶x元,这天的收入:
(23+49)×x
=72×x
=72x(元)
答:这天卖花瓶的收入一共是72x元。
(2)将x=12.5代入式子72x得:72×12.5=900(元)
答:如果每个花瓶12.5元,这天卖花瓶的收入一共是900元。
【点睛】本题主要考查了对单价×数量=总价的理解和灵活运用情况,数字与字母相乘,可以省略乘号,数字写在字母的前面。
3.(1)128a
(2)640米
(3)84米
【分析】(1)速度和×相遇时间=总路程,据此解答。
(2)把a=5代入(1)题的结果进行计算即可。
(3)学校到少年宫490米,用490除以小明的速度求出他到达少年宫所用的时间,再用这个时间乘小丽的速度求出小丽已经走的路程,最后用总路程减去已经走的路程即可求出小丽离少年宫还有多少米。
【详解】(1)(70+58)a=128a(米)
(2)把a=5代入128a,则
128a=128×5
=640
答:小明和小丽家相距640米。
(3)490÷70=7(分)
490-58×7
=490-406
=84(米)
答:小丽离少年宫还有84米。
【点睛】根据“速度和×相遇时间=总路程”即可用含有字母的式子表示小明家和小丽家的距离;明确小明到达少年宫所用的时间就是小丽这时所用的时间是解题的关键。
4.(1)(2x-20)元
(2)80元
【分析】(1)由题意可知:一张桌子的价钱=一把椅子价钱×3-20元,代入未知数表示出桌子的价钱,再求差即可;
(2)将x=50代入(1)中求值即可。
【详解】(1)3×x-20-x=2x-20
答:一张桌子比一把椅子贵2x-20元。
(2)当x=50时,2x-20=2×50-20=80(元)
答:当x=50时,一张桌子比一把椅子贵80元。
【点睛】本题主要考查含有字母式子的化简与求值。
5.(1)a2+ab平方厘米;(2)216平方厘米
【分析】(1)正方形的面积=边长×边长;长方形的面积=长×宽,据此计算正方形和长方形的面积,再相加;
(2)把数据代入到含有字母的式子中,计算即可。
【详解】(1)涂色部分的面积是:a2+ab平方厘米;
(2)当a=12,b=6时,
a2+ab
=12×12+12×6
=144+72
=216(平方厘米)
【点睛】此题考查的是用字母表示数的意义以及求含有字母的式子的值。
6.(1)y-1;y+7;5y
(2)21;22;23;15;29;图见详解
【分析】(1)观察表格中数与数之间的规律可以发现,上下两个相邻数之间相差7,左右两个相邻数之间相差1,据此写出左边数和下边数,求出5个数的和;
(2)根据表格中数与数之间的规律,求出中间数,再根据规律,求出这5个数,再填上方格。
【详解】(1)左边数:y-1,下面数:y+7
(y-1)+y+(y+1)+(y-7)+(y+7)
=y-1+y+y+1+y-7+y+7
=5y
(2)中间数:110÷5=22
左边:22-1=21
右边:22+1=23
上面:22-7=15
下面:22+7=29
【点睛】解答本题的关键是找出表格中的规律,进而求出问题。
7.(1)(9a+21.5b)元;
(2)37元
【分析】(1)总价=单价×数量,再相加即可求出买足球和篮球一共用去了多少元;
(2)当a=60,b=10时,买足球比篮球多用的钱数,用足球的总价减去篮球的总价,即:9a-21.5b,代入式子即可。
【详解】(1)9×a+21.5×b=(9a+21.5b)元
答:买足球和篮球一共用去了(9a+21.5b)元。
(2)当a=28,b=10时,
9a-21.5b
=9×28-21.5×10
=252-215
=37(元)
答:买足球比篮球多用去了37元。
【点睛】解答此题的关键是掌握总价=单价×数量这个公式。
8.15块
【分析】用字母a表示出小班和中班的小朋友人数,则饼干的总块数为6a,如果只分给中班的小朋友,平均每人分得(6+4)块,用除法算式表示出中班小朋友的人数,
小班小朋友的人数=总人数-中班小朋友的人数,小班小朋友每人分得的块数=饼干的总块数÷小班小朋友的人数,据此解答。
【详解】假设小班和中班的小朋友一共有a人,则饼干共6a块
中班小朋友人数:6a÷(6+4)=6a÷10=0.6a(人)
小班小朋友人数:a-0.6a=0.4a(人)
(6a)÷(0.4a)=15(块)
答:如果只分给小班的小朋友,平均每人分得15块。
【点睛】掌握含有字母的式子化简的方法是解答题目的关键。
9.(1)18b平方米
(2)153平方米
【分析】(1)依据长方形的面积公式:S=ab即可求出科学实验室和实验准备室的总面积;
(2)将b=8.5,代入问题(1)中的字母式子里面,即可得解。
【详解】(1)14b+4b=18b(平方米)
答:科学实验室和实验准备室的总面积是18b平方米。
(2)当b=8.5时,18b=18×8.5=153(平方米)
答:当b=8.5时,科学实验室和实验准备室的总面积是153平方米。
【点睛】本题考查用字母表示式子,解题关键是根据已知条件,把未知的数用字母表示出来,然后根据题意列式计算即可。
10.(1)10a;(2)25.2cm或20.4cm
【分析】(1)拼成的大长方形的长是10厘米,宽是a厘米,或者长是5厘米,宽是2a厘米。据此求出这个长方形的面积即可;
(2)根据(1)的分析,将a=2.6分别代入两种情况之中,求出这个长方形的周长。
【详解】(1)2×5×a=10a(平方厘米)
答:这个长方形的面积是10a平方厘米。
(2)①5×2×2+2.6×2
=20+5.2
=25.2(厘米)
②5×2+2.6×2×2
=10+10.4
=20.4(厘米)
答:这个大长方形的周长可能是25.2厘米或者20.4厘米。
【点睛】本题考查了含有字母式子的化简和求值,灵活运用长方形的面积和周长公式是解题的关键。
11.(1)(10a+8b)千克;
(2)320千克
【分析】(1)根据公式:筐数×重量=总重量,把数和字母代入公式即可求出苹果和橘子各多重,之后把苹果和橘子的重量相加即可。
(2)当a=20,b=15时,把a和b的值代入第一问求的式子,算出结果即可。
【详解】(1)苹果重量:10×a=10a(千克)
橘子重量:8×b=8b(千克)
共重:(10a+8b)千克。
答:橘子和苹果一共有:(10a+8b)千克。
(2)当a=20,b=15时
10×20+8×15
=200+120
=320(千克)
答:橘子和苹果一共重320千克。
【点睛】本题主要考查用字母表示数,把给出的字母当做已知数,再根据基本的数量关系解决问题即可,数字和字母之间的乘号可以省略,数字在前,字母在后。
12.3;6
21
过程见详解
【分析】通过数一数可知,当有3条射线时,角的个数有3个;当有4条射线时,角的个数有6个;当有5条射线时,角的个数有10个。由此我可以得出规律:条射线就有角:。
【详解】2条射线有角:(个);
3条射线有角:(个);
4条射线有角:(个);
…
射线条数 2 3 4 …
角的个数 1 3 6 …
所以条射线就有角:。
所以当时,可以形成角:(个)角。
【点睛】本题主要考查数与形的规律,解题时要结合题干,仔细分析,找到变化的规律,再利用规律解题。
13.(1)128-12a;(2)21.44元
【分析】(1)钱包里的余额=微信钱包原有的钱数-发给好朋友的钱数,发给好朋友的钱数=好朋友人数×每人发的钱数。
(2)当时,代入计算即可。
【详解】(1)钱包里的余额:128-12a
(2)当时
128-12a
=128-12×8.88
=128-106.56
=21.44(元)
答:此时余额是21.44元。
【点睛】此题主要考查用字母表示数以及含有字母的式子求值,解答时,把字母当做数,根据数量关系列式即可。
14.(1)10
(2)x+13
【分析】(1)根据题意可知:该图所示是某个月的月历,如果C所在方格内的数字是16,由此向前即可推出A所在的方格的数字是10;
(2)把展开图复原成正方体,则A所对的面是F,然后根据F代表的数字比A代表的数字多(23-10)=13;解答即可。
【详解】如图可知:
(1)A所在的方格的数字是10;
答:A所在方格的数字是10;
(2)把展开图复原成正方体,则A所对的面是F;如果A所在的方格数字是x,则:那么F所在的方格就是x+13;
即:A所对的面的数字是x+13。
【点睛】此题考查了简单图形覆盖现象中的规律,应根据月历中数的排列规律并结合正方体的特征进行解答。
15.(1) (120+10a)千克
(2) 200千克
【详解】(1)120+10a(千克);
答:这个水果店里苹果共有120+10a千克;
(2)当a=8时,代入120+10a,
120+10×8
=120+80
=200(千克);
答:商店一共有200千克苹果.
16.3n+1;301根
【详解】3n+1
当n=100时,3n+1=3×100+1=301.
17.(1)2a
(2)100-2a;90元
【详解】(1)2a
(2)当a=5时,100-2a=100-2×5=90.
18.(1)(30A+38B)个 (2)1210个
【详解】(1)楼上的座位有:30×A=30A(个)
楼下有座位:38×B=38B(个)
剧场共有(30A+38B)个座位.
(2)当A=15时,B=20时,
30A+38B=1210(个)
答:该剧场一共有1210个座位.
19.(1)10+7×0.5=13.5(厘米)
(2)L=10+0.5F
(3)L=10+0.5×100=60(厘米)
【详解】略
20.(1)2x+5x=7x,5x-2x=3x
(2)1400千克,600千克
【详解】略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
