苏科版2023-2024学年九年级上册期末高频考点模拟卷(含解析)
文档属性
| 名称 | 苏科版2023-2024学年九年级上册期末高频考点模拟卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 20:09:50 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末高频考点模拟卷2023-2024学年九年级上册苏科版
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.注意卷面整洁
一、单选题
1.方程的根是( )
A. B. C., D.,
2.将一元二次方程化成一般形式后,常数项为,二次项系数和一次项系数分别是( )
A.5, B.5,4 C.5, D.5,1
3.如图,是的外接圆的直径,若,则等于( )
A. B. C. D.
4.为了落实“双减”政策,一些学校在课后服务时段开设了与冬奥会项目冰壶有关的选修课,如图,在冰壶比赛场地的一端画有一些同心圆作为营垒,其中有两个圆的半径分别约为和,小明掷出一球恰好沿着小圆的切线滑行出界,则该球在大圆内滑行的路径的长度为( )
A.240 B. C.120 D.
5.如图,,是的直径,弦与交于点F,连接,,,,下列三角形中,外心是点O的是( )
A. B. C. D.
6.2023年4月23日是第28个世界读书日.某校举行了演讲大赛,演讲得分按“演讲内容”占、“语言表达”占、“形象风度”占、“整体效果”占进行计算,小芳这四项的得分依次为86,88,90,94,则她的最后得分是( )
A.86分 B.88分 C.90分 D.94分
7.甲、乙两班举行电脑汉字输入比赛参赛学生每分钟并输汉字的个数统计结果如下表:
班级 参加人数 中位数 平均数 方差
甲 55 149 135 191
乙 55 151 135 110
某同学分析上表后得到如下结论:
①甲、乙两班平均成绩相同;
②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字的字数多于150为优秀);
③甲班成绩的波动比乙班大.上述结论中正确的是( )
A.①②③ B.①② C.①③ D.②③
8.已知粉笔盒里只有3支黄色粉笔和2支红色粉笔,每支粉笔除颜色外均相同,现从中任取一支粉笔,则取出黄色粉笔的概率是( ).
A. B. C. D.
二、填空题
9.要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排15场比赛,设有队参加比赛,根据题意,可列方程为 .
10.关于的一元二次方程有两个不相等的实数根,则的取值范围是 .
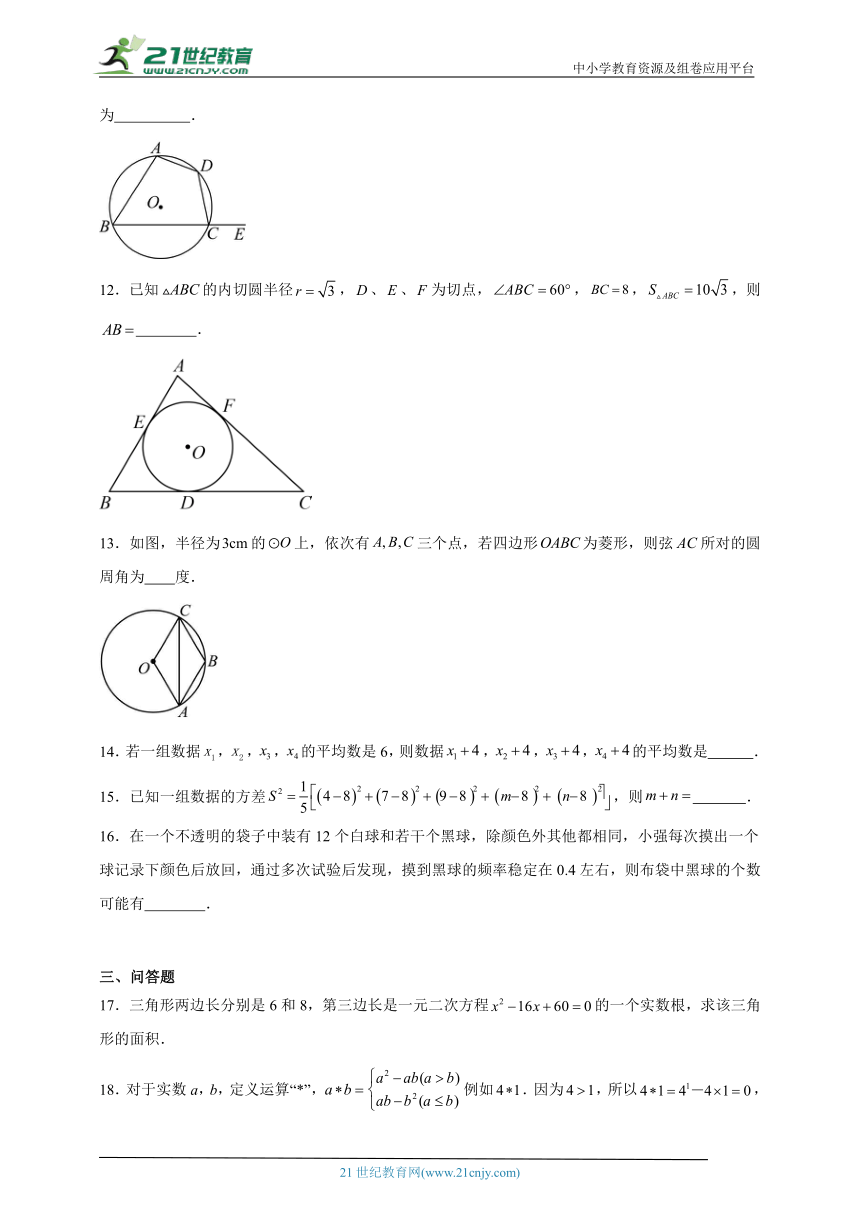
11.如图,四边形内接于,为延长线上的一点,若,则的度数为 .
12.已知的内切圆半径,、、为切点,,,,则 .
13.如图,半径为的上,依次有三个点,若四边形为菱形,则弦所对的圆周角为 度.
14.若一组数据,,,的平均数是6,则数据,,,的平均数是 .
15.已知一组数据的方差,则 .
16.在一个不透明的袋子中装有12个白球和若干个黑球,除颜色外其他都相同,小强每次摸出一个球记录下颜色后放回,通过多次试验后发现,摸到黑球的频率稳定在0.4左右,则布袋中黑球的个数可能有 .
三、问答题
17.三角形两边长分别是6和8,第三边长是一元二次方程的一个实数根,求该三角形的面积.
18.对于实数a,b,定义运算“*”,例如.因为,所以,若是一元二次方程的两个根,求的值.
19.如图,已知为的内切圆,切点分别为D、E、F,且,,,求的半径.
20.2022年冬奥会吉祥物为“冰墩墩”和“雪容融”,体现了人与自然和谐共生,深受青少年的喜爱.现有8张正面印有吉祥物的不透明卡片,卡片除正面图案不同外,其余均相同,其中3张正面印有冰墩墩图案,5张正面印有雪容融图案,将8张卡片正面向下洗匀摆放.
(1)从中随机抽取一张卡片,抽到的卡片恰好是雪容融图案的概率是________;
(2)请你从卡片中取出张冰墩墩卡片,再从剩余的卡片中随机抽出一张,将“抽出的卡片为雪容融”记为事件A,若事件A为必然事件,则m的值为________;若事件A为随机事件,则m的值为________.
21.如图所示的拱桥,用弧表示桥拱.
(1)若弧所在圆的圆心为,是弦的垂直平分线,请你利用尺规作图,找出圆心.(不写作法,但要保留作图痕迹)
(2)若拱桥的跨度(弦的长)为,拱高(弧的中点到弦的距离)为,求拱桥的半径.
22.为了发展体育运动,培养学生的综合能力,某学校成立了足球队、篮球队、射击队等,其中射击队在某次训练中,甲、乙两名队员各射击10发子弹,成绩记录如下表:
射击次序(次) 一 二 三 四 五 六 七 八 九 十
甲的成绩(环) 8 9 7 9 8 6 7 a 10 8
乙的成绩(环) 6 7 9 7 9 10 8 7 7 10
(1)经计算甲和乙的平均成绩都是8环,请求出表中的___________;
(2)甲射击成绩的中位数和乙射击成绩的众数各是多少?
(3)若甲成绩的方差是1.2,请求出乙成绩的方差,判断甲、乙两人谁的成绩更为稳定?
参考答案:
1.C
【分析】根据因式分解法解一元二次方程,即可求解.
【详解】解:,
∴或,
解得:,,
故选:C.
【点睛】本题考查了因式分解法解一元二次方程,熟练掌握解一元二次方程的方法是解题的关键.
2.C
【分析】根据一元二次方程的一般形式是:(a,b,c是常数且).在一般形式中叫二次项,叫一次项,c是常数项.其中a,b,c分别叫二次项系数,一次项系数,常数项求解即可.
【详解】解:,
,
∴二次项系数和一次项系数分别是5,.
故选C.
【点睛】此题主要考查了一元二次方程的一般形式,要确定二次项系数和一次项系数,首先要把方程化成一般形式.
3.B
【分析】根据圆周角定理推论:直径所对圆周角为直角、同圆中等弧所对圆周角相等即可得到结论.
【详解】解:是的外接圆的直径,
点,,,在上,
,
,
是的外接圆的直径,
,
,
故选:B.
【点睛】本题考查了三角形的外接圆与外心,圆周角定理,由圆周角定理得到,是解题的关键.
4.B
【分析】设小圆的切线与小圆相切于点,与大圆交于,连接、,根据切线的性质定理和垂径定理求解即可.
【详解】解:如图,设小圆的切线与小圆相切于点,与大圆交于、,连接、,
,
,
在中,,,
,
,
即该球在大圆内滑行的路径的长度为,
故选B.
【点睛】本题考查切线的性质定理、垂径定理、勾股定理,熟练掌握切线的性质和垂径定理是解答的关键.
5.C
【分析】利用外心的定义,外心:三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心,进而判断得出即可.
【详解】解:只有的三个顶点都在圆上,故外心是点O的是.
故选:C.
【点睛】此题主要考查了三角形外心的定义,正确掌握外心的定义是解题关键.
6.B
【分析】根据加权平均数的计算公式进行计算即可.
【详解】解:∵演讲得分按“演讲内容”占、“语言表达”占、“形象风度”占、“整体效果”占进行计算,
∴她的最后得分为:(分),
故选:B.
【点睛】本题主要考查了加权平均数的计算,解题的关键是熟练掌握加权平均数的计算公式,准确计算.
7.A
【分析】根据平均数,中位数,方差的意义结合表格进行判断即可.
【详解】解:①∵两班的平均数都是135,
∴甲、乙两班平均成绩相同,正确;
②∵甲班的中位数小于150,乙班的中位数大于150,
∴乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字的字数多于150为优秀),正确;
③∵甲班成绩的方差大于乙班,
∴甲班成绩的波动比乙班大,正确;
综上,结论中正确的是①②③,
故选:A.
【点睛】本题考查了平均数,中位数,方差的意义,解题的关键是熟练掌握基本知识,属于中考常考题型.
8.C
【分析】利用概率的公式求解即可.
【详解】解:粉笔盒里只有3支黄色粉笔和2支红色粉笔,共5支粉笔,
从中任取一支粉笔,有5种等可能的结果,
取出黄色粉笔的结果有3种,
∴取出黄色粉笔的概率是,
故选:C.
【点睛】本题考查了用公式求概率,掌握求概率的公式是解题的关键.
9.
【分析】设邀请个球队参加比赛,那么第一个球队和其他球队打场球,第二个球队和其他球队打场,以此类推可以知道共打场球,然后根据计划安排15场比赛即可列出方程.
【详解】解:设邀请个球队参加比赛,
依题意得,
即,
故答案为:.
【点睛】本题考查了由实际问题抽象出一元二次方程,此题和实际生活结合比较紧密,准确找到关键描述语,从而根据等量关系准确地列出方程是解决问题的关键.
10.
【分析】根据一元二次方程的根的判别式,建立关于的不等式,求出的取值范围即可.
【详解】解:∵关于的一元二次方程有两个不相等的实数根,
∴,
解得:.
故答案为:.
【点睛】本题主要考查了一元二次方程根的判别式,掌握一元二次方程根的情况与判别式的关系“时,一元二次方程有两个不相等的实数根”是解题的关键.
11.
【分析】根据圆内接四边形的性质得出,再由同角的补角相等即可得出结果.
【详解】解:∵四边形是圆内接四边形,
∴,
又,
∴,
故答案为.
【点睛】本题主要考查了圆内接四边形的性质,熟知圆内接四边形的对角互补是解决此题的关键.
12.5
【分析】连接、、、、、,根据题意得到,即,进而得出,即可求解.
【详解】解:如图,连接、、、、、,
∵的内切圆半径,、、为切点,,
,
,
,
,
,
,
,,
即,,
故答案为:5.
【点睛】本题考查圆的外接三角形,等腰三角形的性质,圆的切线定理,准确作出辅助线是解题的关键.
13.或
【分析】利用圆周角定理,圆内接四边形和菱形的性质即可求解.
【详解】如图,在优弧取一点,连接,,
∵四边形是菱形,
∴,
∵四边形是圆内接四边形,
∴,
∵,
∴,
∴,,
∴则弦所对的圆周角为或,
故答案为:或.
【点睛】此题考查了圆周角定理,圆内接四边形和菱形的性质,解题的关键是熟练掌握同弧或等弧所对的圆周角是圆心角的一半及菱形的性质及其应用.
14.
【分析】根据求平均数的公式即可列式作答.
【详解】解:依题意,
∵,
∴,
故答案为:.
【点睛】本题考查了求一组数据的平均数,正确掌握求平均数的公式是解题的关键,平均数的公式:.
15.20
【分析】根据方差的公式可以得到平均数,从而算出的值.
【详解】解:由于这组数据的方差是:
,
∴平均数是8.
∴
∴
故答案为:20.
【点睛】本题考查方差的定义与意义:一般地设个数据,,,的平均数为,则方差,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
16.8
【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手,设出未知数列出方程求解.
【详解】解:设袋中有黑球x个,由题意得:
,
解得:,
经检验是原方程的解,
则布袋中黑球的个数可能有8个.
故答案为:8.
【点睛】本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
17.24或
【分析】先解出一元二次方程的两个根,然后分两种情况求出三角形的面积.
【详解】∵
∴
∴
①当三角形的三条边长分别为时,,根据勾股定理的逆定理可知,此时三角形是直角三角形,两条直角的边长为6与8,因此三角形的面积为:.
②当三角形的三条边长分别为时,此时三角形为等腰三角形(如图)
利用勾股定理可求得等腰三角形底边上的高:
因此,三角形的面积为:
∴三角形的面积为24或.
【点睛】本题考查了解一元二次方程、勾股定理及其逆定理,解题的关键是分类讨论思想的运用.
18.或
【分析】解一元二次方程求出,分两种情况和代入解题即可.
【详解】解:解一元二次方程得:,
当时,;
当时,;
∴的值为或.
【点睛】本题考查新定义运算,一元二次方程的解法,解题的关键是掌握一元二次方程的解法.
19.的半径为2.
【分析】连接,由勾股定理可计算出AC的长,根据面积关系,即可求得半径.
【详解】解:如图,连接,
∵为的内切圆,切点分别为D、E、F
∴,且,
在中,由勾股定理得,
∴,
∵
∴
即
∴,
即的半径为2.
【点睛】本题考查了三角形的内切圆,切线的性质,勾股定理,图形的面积等知识,利用面积关系解答是关键.
20.(1)
(2)3;或
【分析】(1)根据概率计算公式进行求解即可;
(2)抽取m张冰墩墩卡片后,抽取一张卡片,当“抽出的卡片为雪容融”为必然事件,那么剩下抽取m张冰墩墩卡片后,则剩下的卡片都是雪容融卡片;当“抽出的卡片为雪容融”为随机事件,那么剩下抽取m张冰墩墩卡片后,则剩下的卡片中还有冰墩墩卡片,据此求解即可.
【详解】(1)解;∵一共有8张卡片,其中有雪容融图案的卡片有5张,且每张卡片被抽到的概率相同,
∴从中随机抽取一张卡片,抽到的卡片恰好是雪容融图案的概率是,
故答案为:
(2)解:∵从卡片中取出张冰墩墩卡片,再从剩余的卡片中随机抽出一张,“抽出的卡片为雪容融”为必然事件,
∴在抽取张冰墩墩卡片后,剩余的卡片中只有雪容融的卡片,
∴此时;
∵从卡片中取出张冰墩墩卡片,再从剩余的卡片中随机抽出一张,“抽出的卡片为雪容融”为随机事件,
∴在抽取张冰墩墩卡片后,剩余的卡片中还有冰墩墩卡片,
∴,
又∵且m为正整数,
∴或.
【点睛】本题主要考查了简单的概率计算,随机事件和必然事件的定义,在一定条件下,一定会发生的事件叫做必然事件,可能发生也有可能不会发生的事件叫做随机事件.
21.(1)见解析
(2)拱桥的半径为米
【分析】(1)作的垂直平分线,交于点,即可求解;
(2)根据垂径定理得出,,设拱桥的半径为,在中,勾股定理即可求解.
【详解】(1)解:如图所示,作的垂直平分线,交于点,
(2)解:如图,
设为的中点,交于点,
∵,
∴,,
设拱桥的半径为,在中,,,
∵,
∴
解得:
∴拱桥的半径为米.
【点睛】本题考查了确定圆心的位置,垂径定理的应用,掌握以上知识是解题的关键.
22.(1)8
(2)8,7
(3)甲的成绩更为稳定
【分析】(1)根据平均数的定义列出关于a的方程,解之即可;
(2)根据中位数和众数的定义求解即可;
(3)先计算出乙成绩的方差,再根据方差的意义判断即可.
【详解】(1)解:∵甲的平均成绩是8环,
;解得:,
故答案为:8;
(2)甲成绩排序后最中间的两个数据为8和8,
所以甲成绩的中位数是;
乙成绩中出现次数最多的为7,
故乙成绩的众数是7,
(3)乙成绩的方差为:
,
∴,
∵甲和乙的平均成绩都是8环,而甲成绩的方差小于乙成绩的方差,
∴甲的成绩更为稳定.
【点睛】本题考查了方差、中位数以及众数,方差是反映一组数据的波动大小的一个量.方差越大,则数据偏离平均值的程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末高频考点模拟卷2023-2024学年九年级上册苏科版
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.注意卷面整洁
一、单选题
1.方程的根是( )
A. B. C., D.,
2.将一元二次方程化成一般形式后,常数项为,二次项系数和一次项系数分别是( )
A.5, B.5,4 C.5, D.5,1
3.如图,是的外接圆的直径,若,则等于( )
A. B. C. D.
4.为了落实“双减”政策,一些学校在课后服务时段开设了与冬奥会项目冰壶有关的选修课,如图,在冰壶比赛场地的一端画有一些同心圆作为营垒,其中有两个圆的半径分别约为和,小明掷出一球恰好沿着小圆的切线滑行出界,则该球在大圆内滑行的路径的长度为( )
A.240 B. C.120 D.
5.如图,,是的直径,弦与交于点F,连接,,,,下列三角形中,外心是点O的是( )
A. B. C. D.
6.2023年4月23日是第28个世界读书日.某校举行了演讲大赛,演讲得分按“演讲内容”占、“语言表达”占、“形象风度”占、“整体效果”占进行计算,小芳这四项的得分依次为86,88,90,94,则她的最后得分是( )
A.86分 B.88分 C.90分 D.94分
7.甲、乙两班举行电脑汉字输入比赛参赛学生每分钟并输汉字的个数统计结果如下表:
班级 参加人数 中位数 平均数 方差
甲 55 149 135 191
乙 55 151 135 110
某同学分析上表后得到如下结论:
①甲、乙两班平均成绩相同;
②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字的字数多于150为优秀);
③甲班成绩的波动比乙班大.上述结论中正确的是( )
A.①②③ B.①② C.①③ D.②③
8.已知粉笔盒里只有3支黄色粉笔和2支红色粉笔,每支粉笔除颜色外均相同,现从中任取一支粉笔,则取出黄色粉笔的概率是( ).
A. B. C. D.
二、填空题
9.要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排15场比赛,设有队参加比赛,根据题意,可列方程为 .
10.关于的一元二次方程有两个不相等的实数根,则的取值范围是 .
11.如图,四边形内接于,为延长线上的一点,若,则的度数为 .
12.已知的内切圆半径,、、为切点,,,,则 .
13.如图,半径为的上,依次有三个点,若四边形为菱形,则弦所对的圆周角为 度.
14.若一组数据,,,的平均数是6,则数据,,,的平均数是 .
15.已知一组数据的方差,则 .
16.在一个不透明的袋子中装有12个白球和若干个黑球,除颜色外其他都相同,小强每次摸出一个球记录下颜色后放回,通过多次试验后发现,摸到黑球的频率稳定在0.4左右,则布袋中黑球的个数可能有 .
三、问答题
17.三角形两边长分别是6和8,第三边长是一元二次方程的一个实数根,求该三角形的面积.
18.对于实数a,b,定义运算“*”,例如.因为,所以,若是一元二次方程的两个根,求的值.
19.如图,已知为的内切圆,切点分别为D、E、F,且,,,求的半径.
20.2022年冬奥会吉祥物为“冰墩墩”和“雪容融”,体现了人与自然和谐共生,深受青少年的喜爱.现有8张正面印有吉祥物的不透明卡片,卡片除正面图案不同外,其余均相同,其中3张正面印有冰墩墩图案,5张正面印有雪容融图案,将8张卡片正面向下洗匀摆放.
(1)从中随机抽取一张卡片,抽到的卡片恰好是雪容融图案的概率是________;
(2)请你从卡片中取出张冰墩墩卡片,再从剩余的卡片中随机抽出一张,将“抽出的卡片为雪容融”记为事件A,若事件A为必然事件,则m的值为________;若事件A为随机事件,则m的值为________.
21.如图所示的拱桥,用弧表示桥拱.
(1)若弧所在圆的圆心为,是弦的垂直平分线,请你利用尺规作图,找出圆心.(不写作法,但要保留作图痕迹)
(2)若拱桥的跨度(弦的长)为,拱高(弧的中点到弦的距离)为,求拱桥的半径.
22.为了发展体育运动,培养学生的综合能力,某学校成立了足球队、篮球队、射击队等,其中射击队在某次训练中,甲、乙两名队员各射击10发子弹,成绩记录如下表:
射击次序(次) 一 二 三 四 五 六 七 八 九 十
甲的成绩(环) 8 9 7 9 8 6 7 a 10 8
乙的成绩(环) 6 7 9 7 9 10 8 7 7 10
(1)经计算甲和乙的平均成绩都是8环,请求出表中的___________;
(2)甲射击成绩的中位数和乙射击成绩的众数各是多少?
(3)若甲成绩的方差是1.2,请求出乙成绩的方差,判断甲、乙两人谁的成绩更为稳定?
参考答案:
1.C
【分析】根据因式分解法解一元二次方程,即可求解.
【详解】解:,
∴或,
解得:,,
故选:C.
【点睛】本题考查了因式分解法解一元二次方程,熟练掌握解一元二次方程的方法是解题的关键.
2.C
【分析】根据一元二次方程的一般形式是:(a,b,c是常数且).在一般形式中叫二次项,叫一次项,c是常数项.其中a,b,c分别叫二次项系数,一次项系数,常数项求解即可.
【详解】解:,
,
∴二次项系数和一次项系数分别是5,.
故选C.
【点睛】此题主要考查了一元二次方程的一般形式,要确定二次项系数和一次项系数,首先要把方程化成一般形式.
3.B
【分析】根据圆周角定理推论:直径所对圆周角为直角、同圆中等弧所对圆周角相等即可得到结论.
【详解】解:是的外接圆的直径,
点,,,在上,
,
,
是的外接圆的直径,
,
,
故选:B.
【点睛】本题考查了三角形的外接圆与外心,圆周角定理,由圆周角定理得到,是解题的关键.
4.B
【分析】设小圆的切线与小圆相切于点,与大圆交于,连接、,根据切线的性质定理和垂径定理求解即可.
【详解】解:如图,设小圆的切线与小圆相切于点,与大圆交于、,连接、,
,
,
在中,,,
,
,
即该球在大圆内滑行的路径的长度为,
故选B.
【点睛】本题考查切线的性质定理、垂径定理、勾股定理,熟练掌握切线的性质和垂径定理是解答的关键.
5.C
【分析】利用外心的定义,外心:三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心,进而判断得出即可.
【详解】解:只有的三个顶点都在圆上,故外心是点O的是.
故选:C.
【点睛】此题主要考查了三角形外心的定义,正确掌握外心的定义是解题关键.
6.B
【分析】根据加权平均数的计算公式进行计算即可.
【详解】解:∵演讲得分按“演讲内容”占、“语言表达”占、“形象风度”占、“整体效果”占进行计算,
∴她的最后得分为:(分),
故选:B.
【点睛】本题主要考查了加权平均数的计算,解题的关键是熟练掌握加权平均数的计算公式,准确计算.
7.A
【分析】根据平均数,中位数,方差的意义结合表格进行判断即可.
【详解】解:①∵两班的平均数都是135,
∴甲、乙两班平均成绩相同,正确;
②∵甲班的中位数小于150,乙班的中位数大于150,
∴乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字的字数多于150为优秀),正确;
③∵甲班成绩的方差大于乙班,
∴甲班成绩的波动比乙班大,正确;
综上,结论中正确的是①②③,
故选:A.
【点睛】本题考查了平均数,中位数,方差的意义,解题的关键是熟练掌握基本知识,属于中考常考题型.
8.C
【分析】利用概率的公式求解即可.
【详解】解:粉笔盒里只有3支黄色粉笔和2支红色粉笔,共5支粉笔,
从中任取一支粉笔,有5种等可能的结果,
取出黄色粉笔的结果有3种,
∴取出黄色粉笔的概率是,
故选:C.
【点睛】本题考查了用公式求概率,掌握求概率的公式是解题的关键.
9.
【分析】设邀请个球队参加比赛,那么第一个球队和其他球队打场球,第二个球队和其他球队打场,以此类推可以知道共打场球,然后根据计划安排15场比赛即可列出方程.
【详解】解:设邀请个球队参加比赛,
依题意得,
即,
故答案为:.
【点睛】本题考查了由实际问题抽象出一元二次方程,此题和实际生活结合比较紧密,准确找到关键描述语,从而根据等量关系准确地列出方程是解决问题的关键.
10.
【分析】根据一元二次方程的根的判别式,建立关于的不等式,求出的取值范围即可.
【详解】解:∵关于的一元二次方程有两个不相等的实数根,
∴,
解得:.
故答案为:.
【点睛】本题主要考查了一元二次方程根的判别式,掌握一元二次方程根的情况与判别式的关系“时,一元二次方程有两个不相等的实数根”是解题的关键.
11.
【分析】根据圆内接四边形的性质得出,再由同角的补角相等即可得出结果.
【详解】解:∵四边形是圆内接四边形,
∴,
又,
∴,
故答案为.
【点睛】本题主要考查了圆内接四边形的性质,熟知圆内接四边形的对角互补是解决此题的关键.
12.5
【分析】连接、、、、、,根据题意得到,即,进而得出,即可求解.
【详解】解:如图,连接、、、、、,
∵的内切圆半径,、、为切点,,
,
,
,
,
,
,
,,
即,,
故答案为:5.
【点睛】本题考查圆的外接三角形,等腰三角形的性质,圆的切线定理,准确作出辅助线是解题的关键.
13.或
【分析】利用圆周角定理,圆内接四边形和菱形的性质即可求解.
【详解】如图,在优弧取一点,连接,,
∵四边形是菱形,
∴,
∵四边形是圆内接四边形,
∴,
∵,
∴,
∴,,
∴则弦所对的圆周角为或,
故答案为:或.
【点睛】此题考查了圆周角定理,圆内接四边形和菱形的性质,解题的关键是熟练掌握同弧或等弧所对的圆周角是圆心角的一半及菱形的性质及其应用.
14.
【分析】根据求平均数的公式即可列式作答.
【详解】解:依题意,
∵,
∴,
故答案为:.
【点睛】本题考查了求一组数据的平均数,正确掌握求平均数的公式是解题的关键,平均数的公式:.
15.20
【分析】根据方差的公式可以得到平均数,从而算出的值.
【详解】解:由于这组数据的方差是:
,
∴平均数是8.
∴
∴
故答案为:20.
【点睛】本题考查方差的定义与意义:一般地设个数据,,,的平均数为,则方差,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
16.8
【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手,设出未知数列出方程求解.
【详解】解:设袋中有黑球x个,由题意得:
,
解得:,
经检验是原方程的解,
则布袋中黑球的个数可能有8个.
故答案为:8.
【点睛】本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
17.24或
【分析】先解出一元二次方程的两个根,然后分两种情况求出三角形的面积.
【详解】∵
∴
∴
①当三角形的三条边长分别为时,,根据勾股定理的逆定理可知,此时三角形是直角三角形,两条直角的边长为6与8,因此三角形的面积为:.
②当三角形的三条边长分别为时,此时三角形为等腰三角形(如图)
利用勾股定理可求得等腰三角形底边上的高:
因此,三角形的面积为:
∴三角形的面积为24或.
【点睛】本题考查了解一元二次方程、勾股定理及其逆定理,解题的关键是分类讨论思想的运用.
18.或
【分析】解一元二次方程求出,分两种情况和代入解题即可.
【详解】解:解一元二次方程得:,
当时,;
当时,;
∴的值为或.
【点睛】本题考查新定义运算,一元二次方程的解法,解题的关键是掌握一元二次方程的解法.
19.的半径为2.
【分析】连接,由勾股定理可计算出AC的长,根据面积关系,即可求得半径.
【详解】解:如图,连接,
∵为的内切圆,切点分别为D、E、F
∴,且,
在中,由勾股定理得,
∴,
∵
∴
即
∴,
即的半径为2.
【点睛】本题考查了三角形的内切圆,切线的性质,勾股定理,图形的面积等知识,利用面积关系解答是关键.
20.(1)
(2)3;或
【分析】(1)根据概率计算公式进行求解即可;
(2)抽取m张冰墩墩卡片后,抽取一张卡片,当“抽出的卡片为雪容融”为必然事件,那么剩下抽取m张冰墩墩卡片后,则剩下的卡片都是雪容融卡片;当“抽出的卡片为雪容融”为随机事件,那么剩下抽取m张冰墩墩卡片后,则剩下的卡片中还有冰墩墩卡片,据此求解即可.
【详解】(1)解;∵一共有8张卡片,其中有雪容融图案的卡片有5张,且每张卡片被抽到的概率相同,
∴从中随机抽取一张卡片,抽到的卡片恰好是雪容融图案的概率是,
故答案为:
(2)解:∵从卡片中取出张冰墩墩卡片,再从剩余的卡片中随机抽出一张,“抽出的卡片为雪容融”为必然事件,
∴在抽取张冰墩墩卡片后,剩余的卡片中只有雪容融的卡片,
∴此时;
∵从卡片中取出张冰墩墩卡片,再从剩余的卡片中随机抽出一张,“抽出的卡片为雪容融”为随机事件,
∴在抽取张冰墩墩卡片后,剩余的卡片中还有冰墩墩卡片,
∴,
又∵且m为正整数,
∴或.
【点睛】本题主要考查了简单的概率计算,随机事件和必然事件的定义,在一定条件下,一定会发生的事件叫做必然事件,可能发生也有可能不会发生的事件叫做随机事件.
21.(1)见解析
(2)拱桥的半径为米
【分析】(1)作的垂直平分线,交于点,即可求解;
(2)根据垂径定理得出,,设拱桥的半径为,在中,勾股定理即可求解.
【详解】(1)解:如图所示,作的垂直平分线,交于点,
(2)解:如图,
设为的中点,交于点,
∵,
∴,,
设拱桥的半径为,在中,,,
∵,
∴
解得:
∴拱桥的半径为米.
【点睛】本题考查了确定圆心的位置,垂径定理的应用,掌握以上知识是解题的关键.
22.(1)8
(2)8,7
(3)甲的成绩更为稳定
【分析】(1)根据平均数的定义列出关于a的方程,解之即可;
(2)根据中位数和众数的定义求解即可;
(3)先计算出乙成绩的方差,再根据方差的意义判断即可.
【详解】(1)解:∵甲的平均成绩是8环,
;解得:,
故答案为:8;
(2)甲成绩排序后最中间的两个数据为8和8,
所以甲成绩的中位数是;
乙成绩中出现次数最多的为7,
故乙成绩的众数是7,
(3)乙成绩的方差为:
,
∴,
∵甲和乙的平均成绩都是8环,而甲成绩的方差小于乙成绩的方差,
∴甲的成绩更为稳定.
【点睛】本题考查了方差、中位数以及众数,方差是反映一组数据的波动大小的一个量.方差越大,则数据偏离平均值的程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
