人教版九年级数学上册24.3 正多边形和圆 提升练习(无答案)
文档属性
| 名称 | 人教版九年级数学上册24.3 正多边形和圆 提升练习(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 317.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 12:33:41 | ||
图片预览

文档简介
24.3 正多边形和圆 提升练习
一、单选题
1.若O是△ABC的内心,且∠BOC=100°,则∠A=( )
A.20° B.30° C.50° D.60°
2.正六边形的边心距是,则正六边形的边长是( )
A. B.1 C.2 D.
3.一个边长为的正多边形的内角和是其外角和的倍,则这个正多边形的外接圆半径是( )
A. B. C.1 D.21
4.连接正八边形的三个顶点,得到如图所示的图形,下列说法不正确的是( )
A.四边形ABCH与四边形EFGH的周长相等 B.连接HD,则HD平分∠CHE
C.整个图形不是中心对称图形 D.是等边三角形
5.如图,有一个半径为的圆形纸片,若在该纸片上沿虚线剪一个最大正六边形纸片,则这个正六边形纸片的边心距是( ).
A. B. C. D.
6.正六边形的内切圆与外接圆面积之比是( )
A. B. C. D.
7.如图,四边形内接于,若,则的大小为( )
A.36° B.54° C.62° D.72°
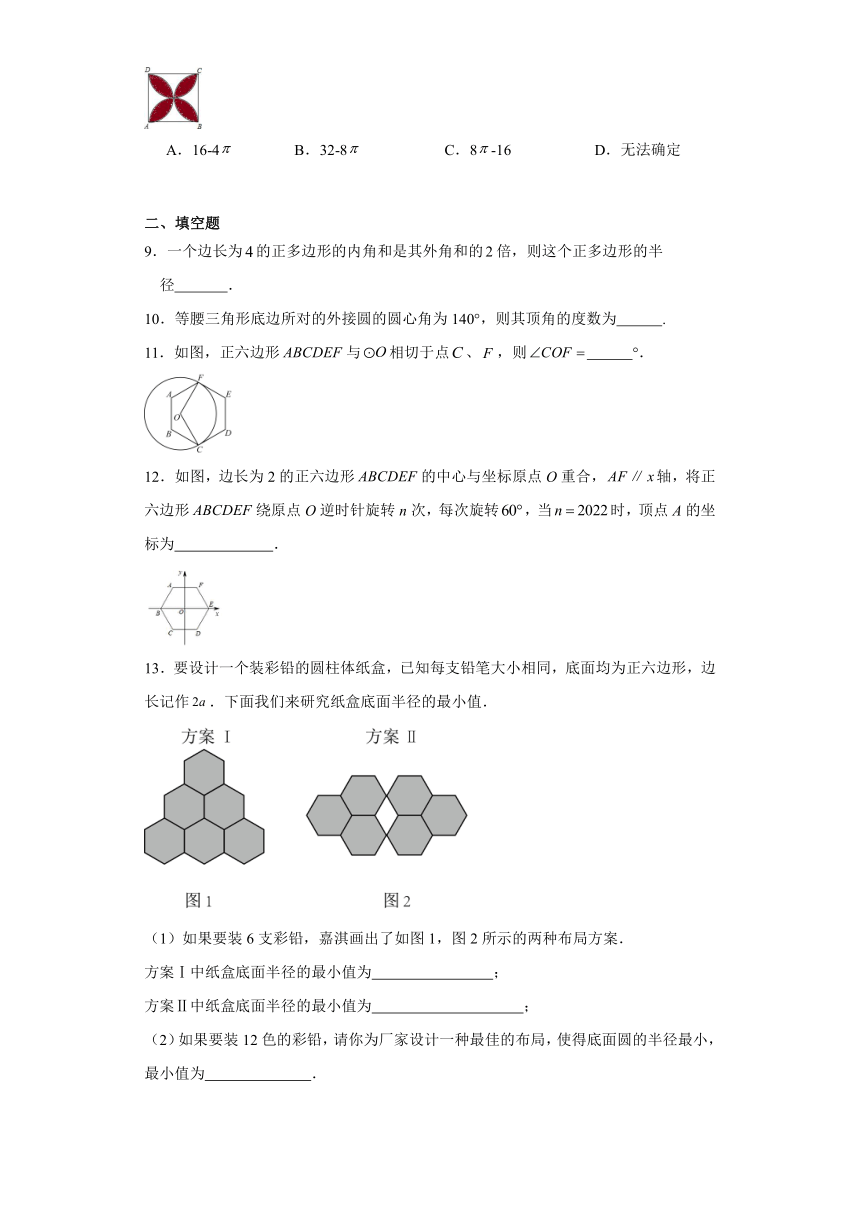
8.. 如图,图中正方形ABCD的边长为4,则图中阴影部分的面积为( )
A.16-4 B.32-8 C.8-16 D.无法确定
二、填空题
9.一个边长为的正多边形的内角和是其外角和的倍,则这个正多边形的半径 .
10.等腰三角形底边所对的外接圆的圆心角为140°,则其顶角的度数为 .
11.如图,正六边形与相切于点、,则 °.
如图,边长为2的正六边形的中心与坐标原点O重合,轴,将正六边形绕原点O逆时针旋转n次,每次旋转,当时,顶点A的坐标为 .
13.要设计一个装彩铅的圆柱体纸盒,已知每支铅笔大小相同,底面均为正六边形,边长记作.下面我们来研究纸盒底面半径的最小值.
(1)如果要装6支彩铅,嘉淇画出了如图1,图2所示的两种布局方案.
方案Ⅰ中纸盒底面半径的最小值为 ;
方案Ⅱ中纸盒底面半径的最小值为 ;
(2)如果要装12色的彩铅,请你为厂家设计一种最佳的布局,使得底面圆的半径最小,最小值为 .
三、解答题
14.如图,求边长为a的正方形的外接圆的半径长.
15.(1)尺规作图:作出⊙O的内接正方形ABCD,使正方形ABCD的对边AD,BC都垂直于EF(见示意图);(说明:不要求写作法,但须保留作图痕迹)
(2)连接EA、EB,求出∠EAD、∠EBC的度数.
16.如图,在半径为10cm的圆中作一个正六边形ABCDEF,试求此正六边形的面积.
17.如图,已知点O是正六边形ABCDEF的对称中心,G,H分别是AF,BC上的点,且AG=BH.
(1)求∠FAB的度数;
(2)求证:OG=OH.
18.某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时,进行如下讨论:
甲同学:这种多边形不一定是正多边形,如圆内接矩形.
乙同学:我发现边数是时,它也不一定是正多边形,如图,是正三角形,,证明六边形的各内角相等,但它未必是正六边形.
丙同学:我能证明,边数是时,它是正多边形,我想…,边数是时,它可能也是正多边形.
请你说明乙同学构造的六边形各内角相等;
请你证明,各内角都相等的圆内接七边形(如图)是正七边形;(不必写已知,求证)
根据以上探索过程,提出你的猜想.(不必证明)
一、单选题
1.若O是△ABC的内心,且∠BOC=100°,则∠A=( )
A.20° B.30° C.50° D.60°
2.正六边形的边心距是,则正六边形的边长是( )
A. B.1 C.2 D.
3.一个边长为的正多边形的内角和是其外角和的倍,则这个正多边形的外接圆半径是( )
A. B. C.1 D.21
4.连接正八边形的三个顶点,得到如图所示的图形,下列说法不正确的是( )
A.四边形ABCH与四边形EFGH的周长相等 B.连接HD,则HD平分∠CHE
C.整个图形不是中心对称图形 D.是等边三角形
5.如图,有一个半径为的圆形纸片,若在该纸片上沿虚线剪一个最大正六边形纸片,则这个正六边形纸片的边心距是( ).
A. B. C. D.
6.正六边形的内切圆与外接圆面积之比是( )
A. B. C. D.
7.如图,四边形内接于,若,则的大小为( )
A.36° B.54° C.62° D.72°
8.. 如图,图中正方形ABCD的边长为4,则图中阴影部分的面积为( )
A.16-4 B.32-8 C.8-16 D.无法确定
二、填空题
9.一个边长为的正多边形的内角和是其外角和的倍,则这个正多边形的半径 .
10.等腰三角形底边所对的外接圆的圆心角为140°,则其顶角的度数为 .
11.如图,正六边形与相切于点、,则 °.
如图,边长为2的正六边形的中心与坐标原点O重合,轴,将正六边形绕原点O逆时针旋转n次,每次旋转,当时,顶点A的坐标为 .
13.要设计一个装彩铅的圆柱体纸盒,已知每支铅笔大小相同,底面均为正六边形,边长记作.下面我们来研究纸盒底面半径的最小值.
(1)如果要装6支彩铅,嘉淇画出了如图1,图2所示的两种布局方案.
方案Ⅰ中纸盒底面半径的最小值为 ;
方案Ⅱ中纸盒底面半径的最小值为 ;
(2)如果要装12色的彩铅,请你为厂家设计一种最佳的布局,使得底面圆的半径最小,最小值为 .
三、解答题
14.如图,求边长为a的正方形的外接圆的半径长.
15.(1)尺规作图:作出⊙O的内接正方形ABCD,使正方形ABCD的对边AD,BC都垂直于EF(见示意图);(说明:不要求写作法,但须保留作图痕迹)
(2)连接EA、EB,求出∠EAD、∠EBC的度数.
16.如图,在半径为10cm的圆中作一个正六边形ABCDEF,试求此正六边形的面积.
17.如图,已知点O是正六边形ABCDEF的对称中心,G,H分别是AF,BC上的点,且AG=BH.
(1)求∠FAB的度数;
(2)求证:OG=OH.
18.某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时,进行如下讨论:
甲同学:这种多边形不一定是正多边形,如圆内接矩形.
乙同学:我发现边数是时,它也不一定是正多边形,如图,是正三角形,,证明六边形的各内角相等,但它未必是正六边形.
丙同学:我能证明,边数是时,它是正多边形,我想…,边数是时,它可能也是正多边形.
请你说明乙同学构造的六边形各内角相等;
请你证明,各内角都相等的圆内接七边形(如图)是正七边形;(不必写已知,求证)
根据以上探索过程,提出你的猜想.(不必证明)
同课章节目录
