北京市昌平区重点中学2023-2024学年高一上学期阶段检测(12月)数学学科试题(无答案)
文档属性
| 名称 | 北京市昌平区重点中学2023-2024学年高一上学期阶段检测(12月)数学学科试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 244.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 22:24:35 | ||
图片预览

文档简介
昌平区重点中学2023-2024学年高一上学期阶段检测
数学学科
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共100分,考试用时90分钟。考试结束后,将本试卷与答题纸一并交回。祝各位考生考试顺利!
第Ⅰ卷
一、选择题(下列各小题中只有一个选项符合题意,共42分,每小题3分)
1.已知集合,,则( )
A. B.
C. D.
2.在范围内,与一角终边相同的角是( )
A. B. C. D.
3.下列函数中,既是偶函数又在上单调递减的是( )
A. B. C. D.
4.命题“,”的否定为( )
A., B.,
C., D.,
5.若角的终边与单位圆相交于点,则等于( )
A. B. C. D.
6.等于( )
A. B. C. D.
7.“且”是“的终边在第二象限”的( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分也非必要条件
8.已知半径为4的扇形面积为,则扇形的圆心角为( )
A. B. C. D.
9.设,,,则( )
A. B. C. D.
10.函数的零点所在的区间为( )
A. B. C. D.
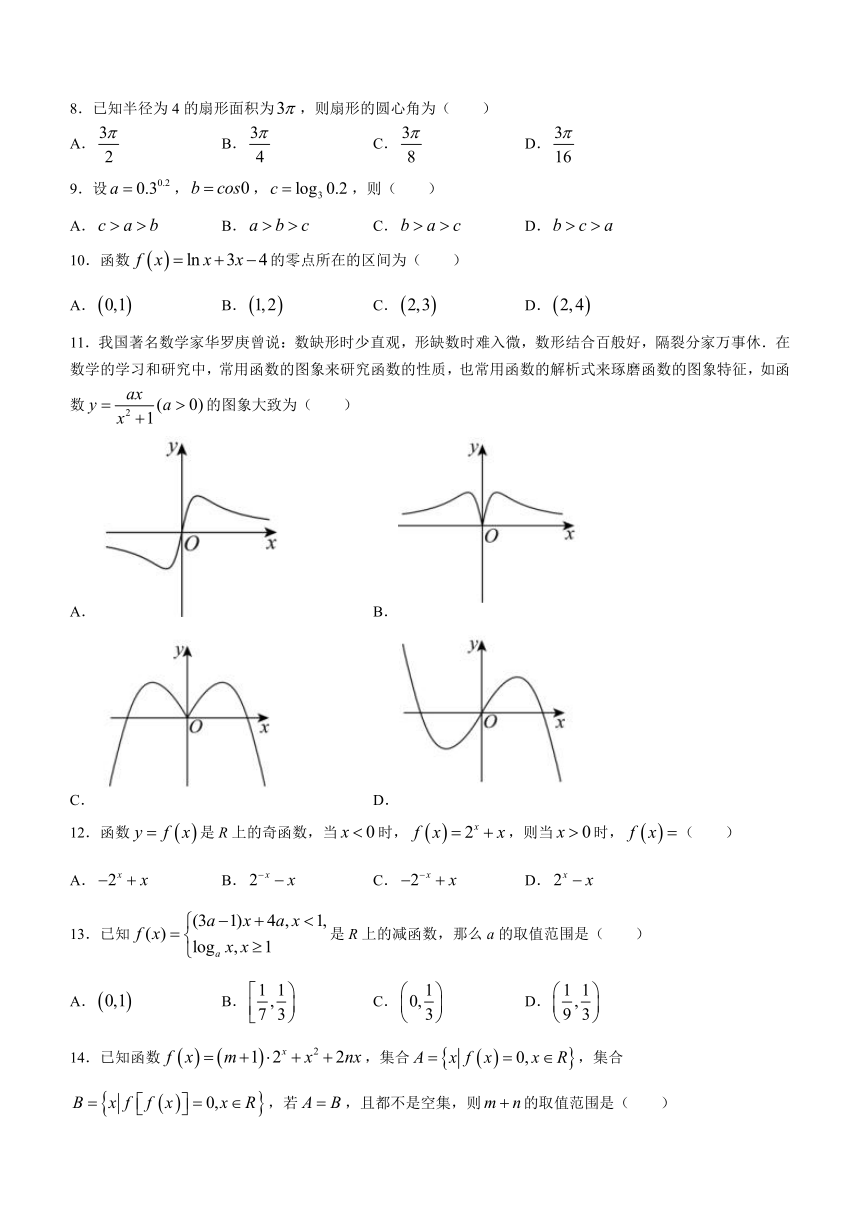
11.我国著名数学家华罗庚曾说:数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休.在数学的学习和研究中,常用函数的图象来研究函数的性质,也常用函数的解析式来琢磨函数的图象特征,如函数的图象大致为( )
A. B.
C. D.
12.函数是R上的奇函数,当时,,则当时,( )
A. B. C. D.
13.已知是R上的减函数,那么a的取值范围是( )
A. B. C. D.
14.已知函数,集合,集合,若,且都不是空集,则的取值范围是( )
A. B. C. D.
第Ⅱ卷
二、填空题(共24分,每小题4分)
15.函数的定义域为______.
16.已知,,则______.
17.函数的递减区间为______.
18.己知,则______.
19.生物学家为了了解某药品对土壤的影响,常通过检测进行判断.已知土壤中某药品的残留量与时间t(年)近似满足关系式,其中a是残留系数,则大约经过______年后土壤中该药品的残留量是2年后残留量的.(参考数据:,答案保留一位小数)
20.世界公认的三大著名数学家为阿基米德、牛顿、高斯,其中享有“数学王子”美誉的高斯提出了取整函数,表示不超过x的最大整数,例如.若,则______﹔已知,,则函数的值域为______.
三、解答题(共34分,第21、22题每题8分,第23、24题每题9分)
21.已知集合,,.
(I)求,:
(Ⅱ)若,求实数m的取值范围.
22.围建一个面积为的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需要维修),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽度为2m的进出口,如图所示.已知旧墙长30米,旧墙的维修费用为45元/m,新墙的造价为180元/m.设利用的旧墙长度为xm,修建此矩形场地围墙的总费用为y元.
(Ⅰ)写出y关于x的函数解析式,并写出函数的定义域;
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
23.定义在R上的函数满足对任意x,,恒有,且时,有.
(Ⅰ)证明:为奇函数;
(Ⅱ)试判断的单调性,并加以证明;
(Ⅲ)若,不等式恒成立,求实数k的取值范围.
24.若函数的定义域为D,集合,若存在非零实数t使得任意都有,且,则称为M上的增长函数.
(Ⅰ)已知函数,函数,直接判断和是否为区间上的,增长函数;
(Ⅱ)已知函数,且是区间上的增长函数,求正整数n的最小值;
(Ⅲ)如果是定义域为R的奇函数,当时,,且为R上的增长函数求实数a的取值范围.
数学学科
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共100分,考试用时90分钟。考试结束后,将本试卷与答题纸一并交回。祝各位考生考试顺利!
第Ⅰ卷
一、选择题(下列各小题中只有一个选项符合题意,共42分,每小题3分)
1.已知集合,,则( )
A. B.
C. D.
2.在范围内,与一角终边相同的角是( )
A. B. C. D.
3.下列函数中,既是偶函数又在上单调递减的是( )
A. B. C. D.
4.命题“,”的否定为( )
A., B.,
C., D.,
5.若角的终边与单位圆相交于点,则等于( )
A. B. C. D.
6.等于( )
A. B. C. D.
7.“且”是“的终边在第二象限”的( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分也非必要条件
8.已知半径为4的扇形面积为,则扇形的圆心角为( )
A. B. C. D.
9.设,,,则( )
A. B. C. D.
10.函数的零点所在的区间为( )
A. B. C. D.
11.我国著名数学家华罗庚曾说:数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休.在数学的学习和研究中,常用函数的图象来研究函数的性质,也常用函数的解析式来琢磨函数的图象特征,如函数的图象大致为( )
A. B.
C. D.
12.函数是R上的奇函数,当时,,则当时,( )
A. B. C. D.
13.已知是R上的减函数,那么a的取值范围是( )
A. B. C. D.
14.已知函数,集合,集合,若,且都不是空集,则的取值范围是( )
A. B. C. D.
第Ⅱ卷
二、填空题(共24分,每小题4分)
15.函数的定义域为______.
16.已知,,则______.
17.函数的递减区间为______.
18.己知,则______.
19.生物学家为了了解某药品对土壤的影响,常通过检测进行判断.已知土壤中某药品的残留量与时间t(年)近似满足关系式,其中a是残留系数,则大约经过______年后土壤中该药品的残留量是2年后残留量的.(参考数据:,答案保留一位小数)
20.世界公认的三大著名数学家为阿基米德、牛顿、高斯,其中享有“数学王子”美誉的高斯提出了取整函数,表示不超过x的最大整数,例如.若,则______﹔已知,,则函数的值域为______.
三、解答题(共34分,第21、22题每题8分,第23、24题每题9分)
21.已知集合,,.
(I)求,:
(Ⅱ)若,求实数m的取值范围.
22.围建一个面积为的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需要维修),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽度为2m的进出口,如图所示.已知旧墙长30米,旧墙的维修费用为45元/m,新墙的造价为180元/m.设利用的旧墙长度为xm,修建此矩形场地围墙的总费用为y元.
(Ⅰ)写出y关于x的函数解析式,并写出函数的定义域;
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
23.定义在R上的函数满足对任意x,,恒有,且时,有.
(Ⅰ)证明:为奇函数;
(Ⅱ)试判断的单调性,并加以证明;
(Ⅲ)若,不等式恒成立,求实数k的取值范围.
24.若函数的定义域为D,集合,若存在非零实数t使得任意都有,且,则称为M上的增长函数.
(Ⅰ)已知函数,函数,直接判断和是否为区间上的,增长函数;
(Ⅱ)已知函数,且是区间上的增长函数,求正整数n的最小值;
(Ⅲ)如果是定义域为R的奇函数,当时,,且为R上的增长函数求实数a的取值范围.
同课章节目录
