6.2 角 同步练习卷 2023-2024学年 苏科版数学七年级上册(含答案)
文档属性
| 名称 | 6.2 角 同步练习卷 2023-2024学年 苏科版数学七年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 923.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 13:03:07 | ||
图片预览


文档简介
6.1 线段、射线、直线同步练习卷(附答案)
一、选择题(本大题共10小题,共30分。在每小题列出的选项中,选出符合题目的一项)
1.在上午时,钟表上的时针与分针的夹角是( )
A. B. C. D.
2.如图,为南偏东方向,,则的方向为( )
A.北偏东 B.北偏东 C.北偏西 D.东偏北
3.等于( )
A. B. C. D.
4.用量角器度量,下列操作正确的是( )
A. B.
C. D.
5.已知三条射线、、,若其中一条射线平分另两条射线所组成的角时,我们称、、组成的图形为“角分图形”.
如图(1),当平分时,图(1)为角分图形.
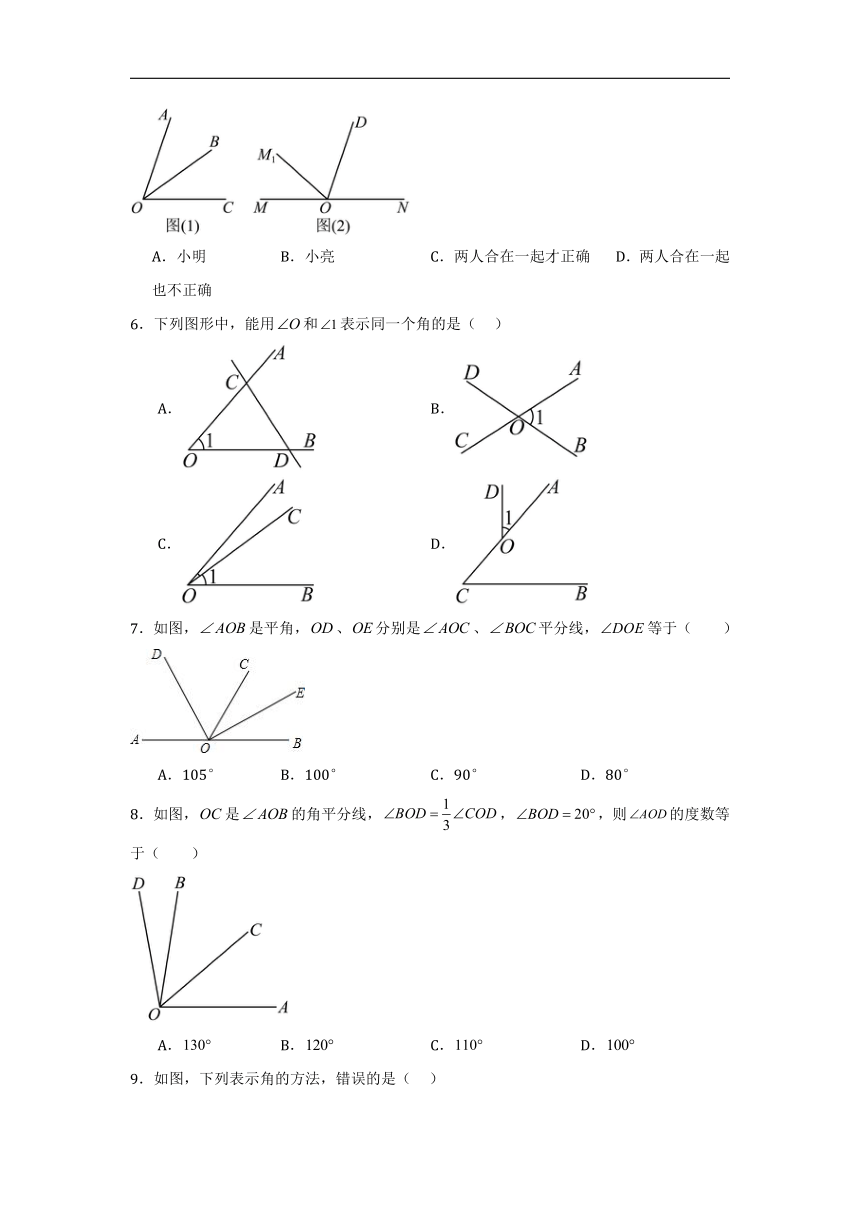
如图(2),点O是直线上一点,,射线绕点O以每秒的速度顺时针旋转至,设时间为,当t为何值时,图中存在角分图形.小明认为,小亮认为,
你认为正确的答案为( )
A.小明 B.小亮 C.两人合在一起才正确 D.两人合在一起也不正确
6.下列图形中,能用和表示同一个角的是( )
A. B.
C. D.
7.如图,是平角,、分别是、平分线,等于( )
A.105° B.100° C.90° D.80°
8.如图,是的角平分线,,,则的度数等于( )
A. B. C. D.
9.如图,下列表示角的方法,错误的是( )
A.与表示同一个角
B.也可用来表示
C.图中共有三个角:,,
D.表示的是
10.如图,已知直线与相交于点F,平分,若,则度数是( )
A. B. C. D.
二、填空题(本大题共8小题,共24分)
11.如图,直线相交于点,,若,则的度数为.
12.如图,点O在直线上,是的平分线,若,则的度数为.
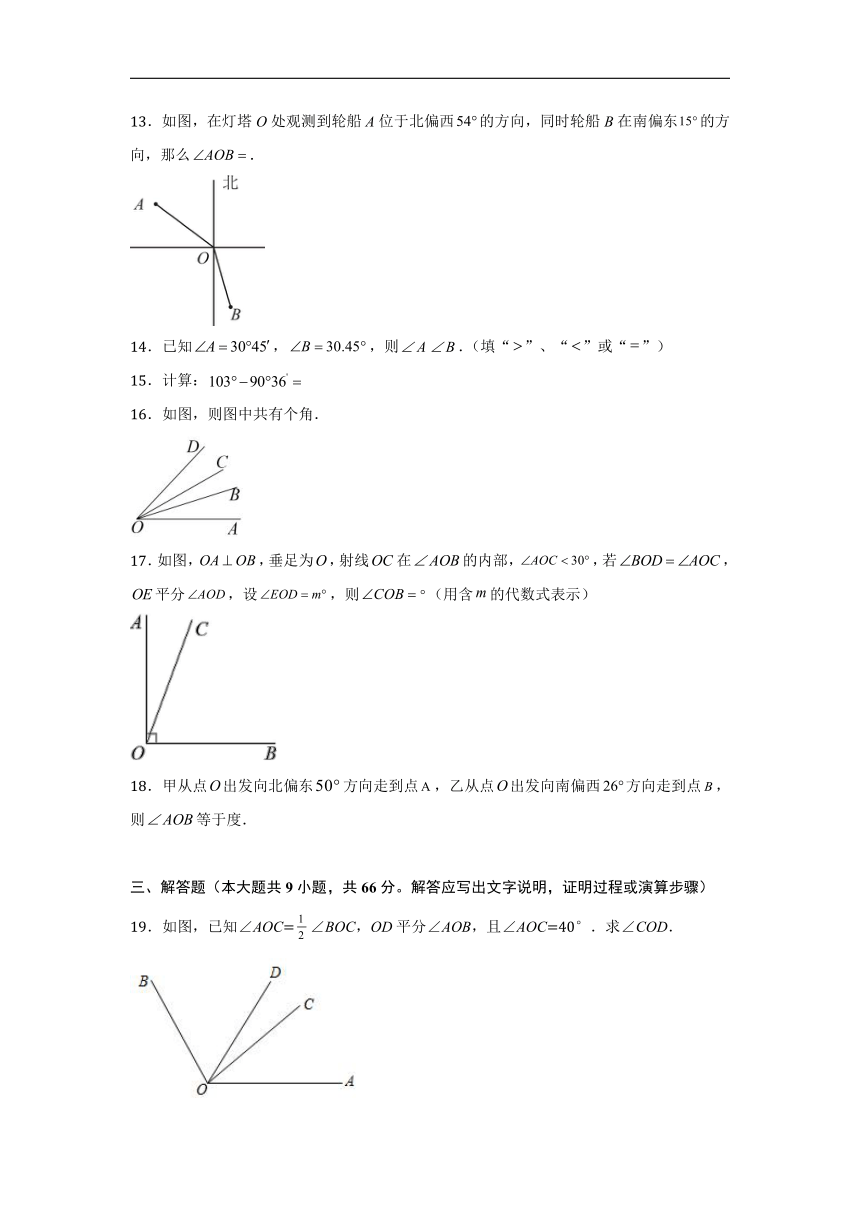
13.如图,在灯塔O处观测到轮船A位于北偏西的方向,同时轮船B在南偏东的方向,那么.
14.已知,,则.(填“”、“”或“”)
15.计算:
16.如图,则图中共有个角.
17.如图,,垂足为,射线在的内部,,若,平分,设,则(用含的代数式表示)
18.甲从点出发向北偏东方向走到点,乙从点出发向南偏西方向走到点,则等于度.
三、解答题(本大题共9小题,共66分。解答应写出文字说明,证明过程或演算步骤)
19.如图,已知∠AOC=∠BOC,OD平分∠AOB,且∠AOC=40°.求∠COD.
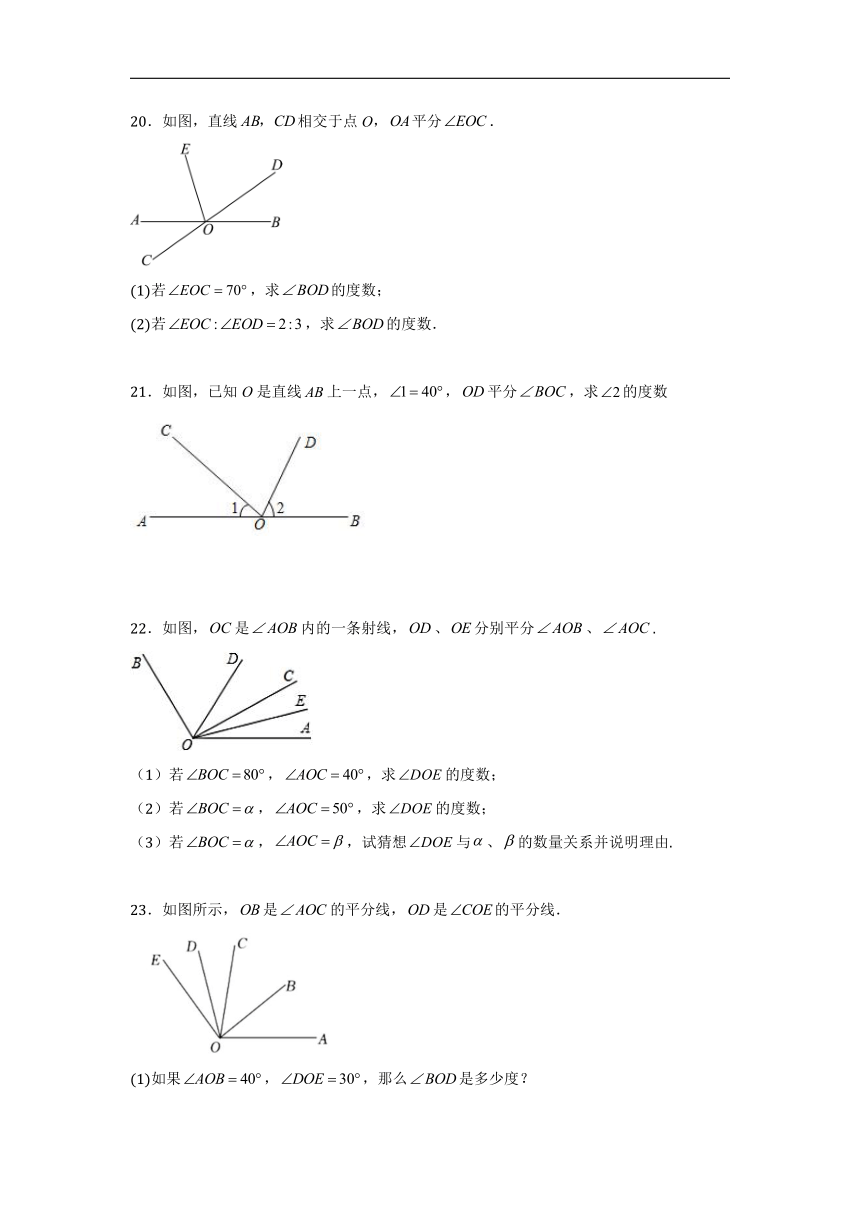
20.如图,直线相交于点O,平分.
(1)若,求的度数;
(2)若,求的度数.
21.如图,已知O是直线上一点,,平分,求的度数
22.如图,是内的一条射线,、分别平分、.
(1)若,,求的度数;
(2)若,,求的度数;
(3)若,,试猜想与、的数量关系并说明理由.
23.如图所示,是的平分线,是的平分线.
(1)如果,,那么是多少度?
(2)如果,,那么是多少度?
24.如图,,是的平分线,是的平分线,.
(1)求的度数;
(2)求的度数;
25.如图所示,直线AB,CD相交于点O,平分,射线在内部.
(1)若,求的度数.
(2)若,求的度数.
26.定义:如图1,射线在的内部,图中共有3个角:和,若其中有一个角的度数是另一个角度数的两倍,则称射线在的“妙分线”.
(1)如图1,若,且射线在的“妙分线”,求的度数.
(2)如图2,若,射线绕点P从位置开始,以每秒8°的速度顺时针旋转,同时,射线绕点P以每秒的速度顺时针旋转,当与成时,射线,射线同时停止旋转,设旋转的时间为t秒,求t为何值时,射线是的“妙分线”.
27.【阅读材料】:
如图1,将线段放在直线上,然后将线段绕点O按如下方式旋转:第1步,从(在上)开始先顺时针旋转锐角至;第2步,从开始继续同向旋转至;第3步,从开始继续旋转至,….当转到位置时弹回,逆时针向位置旋转;当转到位置时再弹回,继续向位置旋转,…如此反复.
例如:当时, 的位置如图2所示,其中第4步旋转到后弹回,即.
【解决问题】:
(1)当时,的位置如图3所示.
①,;
②求出的度数.
(2)当时, 且,则的值为;
(3)若在整个旋转过程中, 是第一次经过弹回后而得到的位置,则的范围是;(请用“>”,“<”,“≥”,“≤”进行表示)
参考答案:
1.C
2.A
3.C
4.D
5.D
6.A
7.C
8.D
9.B
10.C
11.
12./20度
13./141度
14.
15.
16.
17.或
18.156
19.∠COD=20°
【详解】解:∵∠AOC=∠BOC,∠AOC=40°,
∴∠BOC=80°,
∴∠AOB=∠BOC+∠AOC=120°;
∵OD平分∠AOB,
∴∠AOD=∠AOB=60°,
∴∠COD=∠AOD﹣∠AOC=20°.
20.(1)(2)
【详解】(1)解:平分,
,
;
(2)解:设,则,
根据题意得,
解得:,
,
,
.
21.
【详解】解:∵,
∴,
∵平分,
∴.
22.(1);(2);(3),与无关
【详解】解:(1),
、分别平分、
所以的度数.
(2),
、分别平分、
所以的度数.
(3),
、分别平分、
所以,与无关.
23.(1)(2)
【详解】(1)解:∵是的平分线,是的平分线,,,
∴,,
∴;
(2)解:∵是的平分线,,
∴,
∵,
∴,
∵是的平分线,
∴.
24.(1);
(2).
【详解】(1)解:∵,是的平分线,
∴;
(2)解:∵是的平分线,是的平分线,
∴,,
∴.
25.(1)118°
(2)110°
【详解】(1)∵∠AOC=56°,
∴∠AOD=180°-∠AOC=124°,∠BOD=56°,
∵OE平分∠AOD,
∴∠AOE=∠DOE=∠AOD=62°,
∴∠BOE=∠BOD+∠DOE=118°,
即∠BOE为118°;
(2)设∠FOB=x,
∵∠EOD:∠FOD:∠FOB=7:3:1,
∴∠EOD=7x,∠FOD=3x,
∵OE平分∠AOD,
∴∠AOE=∠DOE=∠AOD
∴∠AOE=7x,
∵∠AOE+∠DOE+∠DOF+∠BOF=180°,
∴7x+7x+3x+x=180°,
∴x=10°,
∵∠COE=∠COA+∠AOE,∠AOC=∠BOD,
∴∠COE=∠BOD+∠AOE=∠BOF+∠FOD+∠AOE=x+3x+7x=11x=110°,
即∠COE为110°.
26.(1)或或
(2)当t为或6或10时,射线是的“妙分线”
【详解】(1)解:∵,且射线在的“妙分线”,
∴或或,
∴或或;
(2)解:根据题意得:
当时,有
,解得;
当时,有
,解得;
当时,有
,解得.
故当t为或6或10时,射线是的“妙分线”.
27.(1)①;;②
(2);;
(3)
【详解】(1)解:①当时,,,
故答案为:;;
②∵,
∴,
故答案为:
(2)①当都不从弹回时,
则,
∴,
②当在右边时,
则,
解得
③当在左边时,
则,
解得
综上可知,的值为或或,
故答案为:;;
(3)当在或的右边时,
则,
解得,
当在与 之间时,
则,
解得,
当在或者与之间时,
则,
解得,
当在或或与之间时,
则,
解得,
若在整个旋转过程中, 是第一次经过弹回后而得到的位置,则的范围是,
故答案为:
一、选择题(本大题共10小题,共30分。在每小题列出的选项中,选出符合题目的一项)
1.在上午时,钟表上的时针与分针的夹角是( )
A. B. C. D.
2.如图,为南偏东方向,,则的方向为( )
A.北偏东 B.北偏东 C.北偏西 D.东偏北
3.等于( )
A. B. C. D.
4.用量角器度量,下列操作正确的是( )
A. B.
C. D.
5.已知三条射线、、,若其中一条射线平分另两条射线所组成的角时,我们称、、组成的图形为“角分图形”.
如图(1),当平分时,图(1)为角分图形.
如图(2),点O是直线上一点,,射线绕点O以每秒的速度顺时针旋转至,设时间为,当t为何值时,图中存在角分图形.小明认为,小亮认为,
你认为正确的答案为( )
A.小明 B.小亮 C.两人合在一起才正确 D.两人合在一起也不正确
6.下列图形中,能用和表示同一个角的是( )
A. B.
C. D.
7.如图,是平角,、分别是、平分线,等于( )
A.105° B.100° C.90° D.80°
8.如图,是的角平分线,,,则的度数等于( )
A. B. C. D.
9.如图,下列表示角的方法,错误的是( )
A.与表示同一个角
B.也可用来表示
C.图中共有三个角:,,
D.表示的是
10.如图,已知直线与相交于点F,平分,若,则度数是( )
A. B. C. D.
二、填空题(本大题共8小题,共24分)
11.如图,直线相交于点,,若,则的度数为.
12.如图,点O在直线上,是的平分线,若,则的度数为.
13.如图,在灯塔O处观测到轮船A位于北偏西的方向,同时轮船B在南偏东的方向,那么.
14.已知,,则.(填“”、“”或“”)
15.计算:
16.如图,则图中共有个角.
17.如图,,垂足为,射线在的内部,,若,平分,设,则(用含的代数式表示)
18.甲从点出发向北偏东方向走到点,乙从点出发向南偏西方向走到点,则等于度.
三、解答题(本大题共9小题,共66分。解答应写出文字说明,证明过程或演算步骤)
19.如图,已知∠AOC=∠BOC,OD平分∠AOB,且∠AOC=40°.求∠COD.
20.如图,直线相交于点O,平分.
(1)若,求的度数;
(2)若,求的度数.
21.如图,已知O是直线上一点,,平分,求的度数
22.如图,是内的一条射线,、分别平分、.
(1)若,,求的度数;
(2)若,,求的度数;
(3)若,,试猜想与、的数量关系并说明理由.
23.如图所示,是的平分线,是的平分线.
(1)如果,,那么是多少度?
(2)如果,,那么是多少度?
24.如图,,是的平分线,是的平分线,.
(1)求的度数;
(2)求的度数;
25.如图所示,直线AB,CD相交于点O,平分,射线在内部.
(1)若,求的度数.
(2)若,求的度数.
26.定义:如图1,射线在的内部,图中共有3个角:和,若其中有一个角的度数是另一个角度数的两倍,则称射线在的“妙分线”.
(1)如图1,若,且射线在的“妙分线”,求的度数.
(2)如图2,若,射线绕点P从位置开始,以每秒8°的速度顺时针旋转,同时,射线绕点P以每秒的速度顺时针旋转,当与成时,射线,射线同时停止旋转,设旋转的时间为t秒,求t为何值时,射线是的“妙分线”.
27.【阅读材料】:
如图1,将线段放在直线上,然后将线段绕点O按如下方式旋转:第1步,从(在上)开始先顺时针旋转锐角至;第2步,从开始继续同向旋转至;第3步,从开始继续旋转至,….当转到位置时弹回,逆时针向位置旋转;当转到位置时再弹回,继续向位置旋转,…如此反复.
例如:当时, 的位置如图2所示,其中第4步旋转到后弹回,即.
【解决问题】:
(1)当时,的位置如图3所示.
①,;
②求出的度数.
(2)当时, 且,则的值为;
(3)若在整个旋转过程中, 是第一次经过弹回后而得到的位置,则的范围是;(请用“>”,“<”,“≥”,“≤”进行表示)
参考答案:
1.C
2.A
3.C
4.D
5.D
6.A
7.C
8.D
9.B
10.C
11.
12./20度
13./141度
14.
15.
16.
17.或
18.156
19.∠COD=20°
【详解】解:∵∠AOC=∠BOC,∠AOC=40°,
∴∠BOC=80°,
∴∠AOB=∠BOC+∠AOC=120°;
∵OD平分∠AOB,
∴∠AOD=∠AOB=60°,
∴∠COD=∠AOD﹣∠AOC=20°.
20.(1)(2)
【详解】(1)解:平分,
,
;
(2)解:设,则,
根据题意得,
解得:,
,
,
.
21.
【详解】解:∵,
∴,
∵平分,
∴.
22.(1);(2);(3),与无关
【详解】解:(1),
、分别平分、
所以的度数.
(2),
、分别平分、
所以的度数.
(3),
、分别平分、
所以,与无关.
23.(1)(2)
【详解】(1)解:∵是的平分线,是的平分线,,,
∴,,
∴;
(2)解:∵是的平分线,,
∴,
∵,
∴,
∵是的平分线,
∴.
24.(1);
(2).
【详解】(1)解:∵,是的平分线,
∴;
(2)解:∵是的平分线,是的平分线,
∴,,
∴.
25.(1)118°
(2)110°
【详解】(1)∵∠AOC=56°,
∴∠AOD=180°-∠AOC=124°,∠BOD=56°,
∵OE平分∠AOD,
∴∠AOE=∠DOE=∠AOD=62°,
∴∠BOE=∠BOD+∠DOE=118°,
即∠BOE为118°;
(2)设∠FOB=x,
∵∠EOD:∠FOD:∠FOB=7:3:1,
∴∠EOD=7x,∠FOD=3x,
∵OE平分∠AOD,
∴∠AOE=∠DOE=∠AOD
∴∠AOE=7x,
∵∠AOE+∠DOE+∠DOF+∠BOF=180°,
∴7x+7x+3x+x=180°,
∴x=10°,
∵∠COE=∠COA+∠AOE,∠AOC=∠BOD,
∴∠COE=∠BOD+∠AOE=∠BOF+∠FOD+∠AOE=x+3x+7x=11x=110°,
即∠COE为110°.
26.(1)或或
(2)当t为或6或10时,射线是的“妙分线”
【详解】(1)解:∵,且射线在的“妙分线”,
∴或或,
∴或或;
(2)解:根据题意得:
当时,有
,解得;
当时,有
,解得;
当时,有
,解得.
故当t为或6或10时,射线是的“妙分线”.
27.(1)①;;②
(2);;
(3)
【详解】(1)解:①当时,,,
故答案为:;;
②∵,
∴,
故答案为:
(2)①当都不从弹回时,
则,
∴,
②当在右边时,
则,
解得
③当在左边时,
则,
解得
综上可知,的值为或或,
故答案为:;;
(3)当在或的右边时,
则,
解得,
当在与 之间时,
则,
解得,
当在或者与之间时,
则,
解得,
当在或或与之间时,
则,
解得,
若在整个旋转过程中, 是第一次经过弹回后而得到的位置,则的范围是,
故答案为:
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
