1.3.1 课时1 有理数的加法法则 课件(15张PPT) 人教版数学七年级上册
文档属性
| 名称 | 1.3.1 课时1 有理数的加法法则 课件(15张PPT) 人教版数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 424.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 14:20:25 | ||
图片预览



文档简介
(共15张PPT)
1.3.1 有理数的加法
第一章 有理数
课时1 有理数的加法法则
学习目标
1.了解有理数加法的意义.
2.能运用有理数加法法则准确进行有理数的加法运算.
新课导入
+1
-1
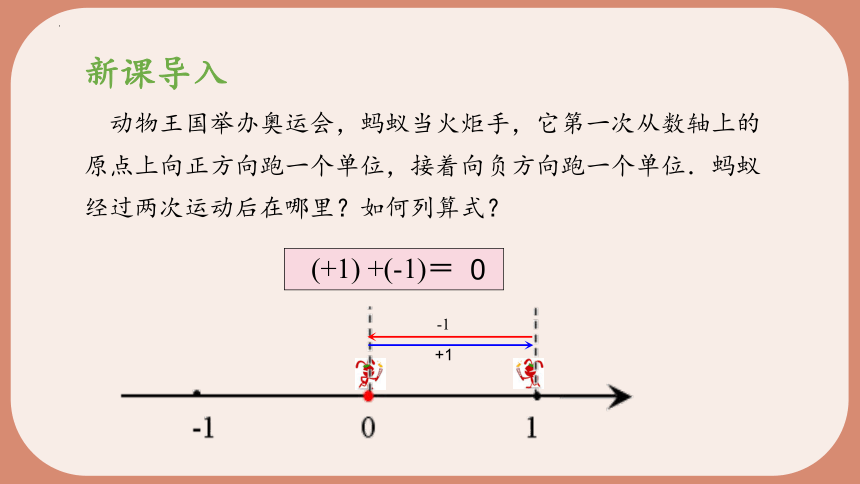
(+1) +(-1)=
0
动物王国举办奥运会,蚂蚁当火炬手,它第一次从数轴上的原点上向正方向跑一个单位,接着向负方向跑一个单位.蚂蚁经过两次运动后在哪里?如何列算式?
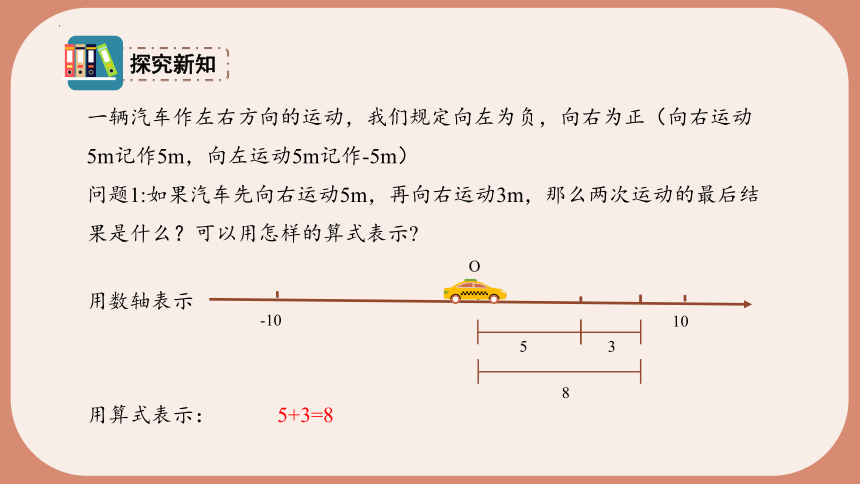
一辆汽车作左右方向的运动,我们规定向左为负,向右为正(向右运动5m记作5m,向左运动5m记作-5m)
问题1:如果汽车先向右运动5m,再向右运动3m,那么两次运动的最后结果是什么?可以用怎样的算式表示
8
用数轴表示
用算式表示:
3
5
O
10
-10
5+3=8
探究新知
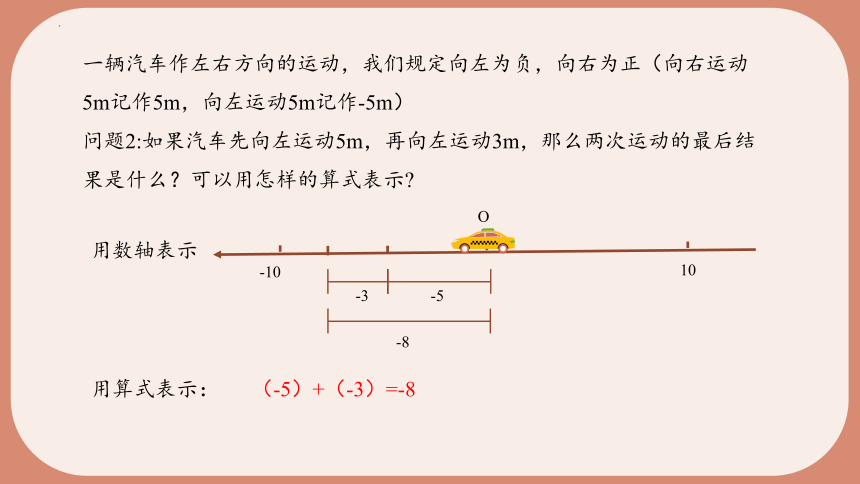
一辆汽车作左右方向的运动,我们规定向左为负,向右为正(向右运动5m记作5m,向左运动5m记作-5m)
问题2:如果汽车先向左运动5m,再向左运动3m,那么两次运动的最后结果是什么?可以用怎样的算式表示
-8
用数轴表示
用算式表示: (-5)+(-3)=-8
-3
-5
O
-10
10
探究一:观察以上两个算式,完成以下3个问题。
(1)每个算式中两个加数的符号有什么关系?
(2)每个算式中结果的符号与两个加数的符号有什么关系?
(3)每个算式中结果的绝对值与两个加数的绝对值有什么关系?
相同
相同
结果的绝对值等于两个加数的绝对值的和
法则: 同号两数相加,取相同的符号,并把绝对值相加.
(+5) + (+3) =
+8
(- 5) + (-3) =
-8
加数
加数
结果
↓
↓
↓
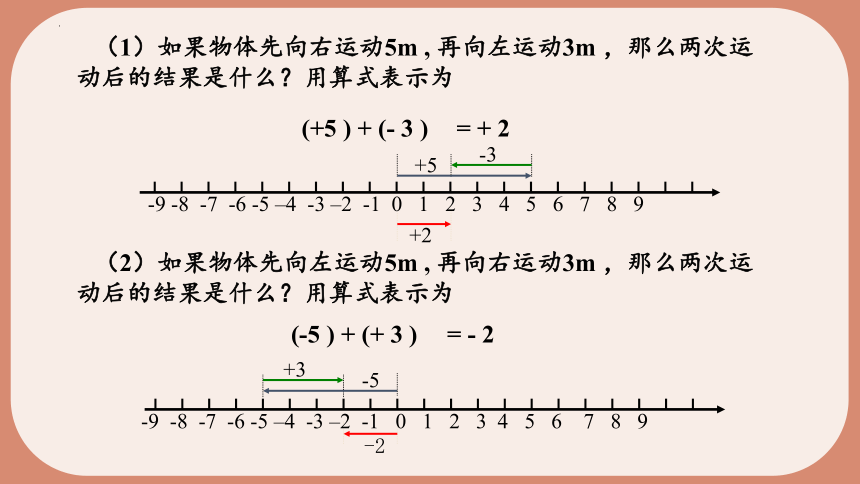
(1)如果物体先向右运动5m , 再向左运动3m ,那么两次运动后的结果是什么?用算式表示为
(2)如果物体先向左运动5m , 再向右运动3m ,那么两次运动后的结果是什么?用算式表示为
(+5 ) + (- 3 )
(-5 ) + (+ 3 )
+2
+5
-3
-9 -8 -7 -6 -5 –4 -3 –2 -1 0 1 2 3 4 5 6 7 8 9
= + 2
+3
-5
-2
= - 2
-9 -8 -7 -6 -5 –4 -3 –2 -1 0 1 2 3 4 5 6 7 8 9
根据以上两个算式能否尝试总结异号两数相加的法则?
注意关注加数的符号和绝对值
绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值;
结论:
5+(-3)= 2
(-5)+3=-2
归纳总结
练一练
(1) (-5)+ 9
= +( )
(2) 6 + (-10)
= -( )
(1) (-5)+ 9
(2) 6 + (-10)
解:
9-5
=4
10-6
=-4
问题:如果小猪先向西行走2米,再继续向东行走2米,则小猪两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-3 -2
东
(-2)+(+2)= 0(米)
解:小猪一共行走了0米.写成算式为:
-2 + (+2)= (2-2)
加数异号
你从上面式子中发现了什么?
知识点一:有理数加法法则二
加数
加数
和
异号两数相加,绝对值相等时和为0.
1.两个有理数的和为零,则这两个有理数一定( )
A.都是零 B.至少有一个是零
C.一正一负 D.互为相反数
2.在1,-1,-2这三个数中,任意两数之和的最大值是( )
A.1 B.0 C.-1 D.3
D
B
当堂检测
A. a+c<0 B. b+c<0 C. -b+a<0 D.-a+b+c<0
3.已知有理数a,b,c在数轴上的位置如图所示,则下列结论中错误的是( )
A.1 B.-5 C.-5或-1 D.5或1
4.若│x│= 3,│y│= 2,且x>y,则x+y的值为( )
C
D
(1)(-0.6)+(-2.7); (2)3.7+(-8.4);
(3)3.22+1.78; (4)7+(-3.3).
5.计算
答案:(1)-3.3 (2)-4.7 (3)5 (4)3.7
解:中午的气温为-25+11=-14(℃),
夜间的气温为-14+(-13)=-27(℃)
6.某城市一天早晨的气温是-25℃,中午上升了11℃,夜间又下降了13℃,那么这天中午、夜间的气温分别是多少?
课堂总结
确定类型 定符号 绝对值
同号
异号(绝对值不相等)
异号(互为相反数) 与0相加 相同符号
取绝对值较大的加数的符号
相加
相减
结果是0
仍是这个数
有理数的加法法则:
1.3.1 有理数的加法
第一章 有理数
课时1 有理数的加法法则
学习目标
1.了解有理数加法的意义.
2.能运用有理数加法法则准确进行有理数的加法运算.
新课导入
+1
-1
(+1) +(-1)=
0
动物王国举办奥运会,蚂蚁当火炬手,它第一次从数轴上的原点上向正方向跑一个单位,接着向负方向跑一个单位.蚂蚁经过两次运动后在哪里?如何列算式?
一辆汽车作左右方向的运动,我们规定向左为负,向右为正(向右运动5m记作5m,向左运动5m记作-5m)
问题1:如果汽车先向右运动5m,再向右运动3m,那么两次运动的最后结果是什么?可以用怎样的算式表示
8
用数轴表示
用算式表示:
3
5
O
10
-10
5+3=8
探究新知
一辆汽车作左右方向的运动,我们规定向左为负,向右为正(向右运动5m记作5m,向左运动5m记作-5m)
问题2:如果汽车先向左运动5m,再向左运动3m,那么两次运动的最后结果是什么?可以用怎样的算式表示
-8
用数轴表示
用算式表示: (-5)+(-3)=-8
-3
-5
O
-10
10
探究一:观察以上两个算式,完成以下3个问题。
(1)每个算式中两个加数的符号有什么关系?
(2)每个算式中结果的符号与两个加数的符号有什么关系?
(3)每个算式中结果的绝对值与两个加数的绝对值有什么关系?
相同
相同
结果的绝对值等于两个加数的绝对值的和
法则: 同号两数相加,取相同的符号,并把绝对值相加.
(+5) + (+3) =
+8
(- 5) + (-3) =
-8
加数
加数
结果
↓
↓
↓
(1)如果物体先向右运动5m , 再向左运动3m ,那么两次运动后的结果是什么?用算式表示为
(2)如果物体先向左运动5m , 再向右运动3m ,那么两次运动后的结果是什么?用算式表示为
(+5 ) + (- 3 )
(-5 ) + (+ 3 )
+2
+5
-3
-9 -8 -7 -6 -5 –4 -3 –2 -1 0 1 2 3 4 5 6 7 8 9
= + 2
+3
-5
-2
= - 2
-9 -8 -7 -6 -5 –4 -3 –2 -1 0 1 2 3 4 5 6 7 8 9
根据以上两个算式能否尝试总结异号两数相加的法则?
注意关注加数的符号和绝对值
绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值;
结论:
5+(-3)= 2
(-5)+3=-2
归纳总结
练一练
(1) (-5)+ 9
= +( )
(2) 6 + (-10)
= -( )
(1) (-5)+ 9
(2) 6 + (-10)
解:
9-5
=4
10-6
=-4
问题:如果小猪先向西行走2米,再继续向东行走2米,则小猪两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-3 -2
东
(-2)+(+2)= 0(米)
解:小猪一共行走了0米.写成算式为:
-2 + (+2)= (2-2)
加数异号
你从上面式子中发现了什么?
知识点一:有理数加法法则二
加数
加数
和
异号两数相加,绝对值相等时和为0.
1.两个有理数的和为零,则这两个有理数一定( )
A.都是零 B.至少有一个是零
C.一正一负 D.互为相反数
2.在1,-1,-2这三个数中,任意两数之和的最大值是( )
A.1 B.0 C.-1 D.3
D
B
当堂检测
A. a+c<0 B. b+c<0 C. -b+a<0 D.-a+b+c<0
3.已知有理数a,b,c在数轴上的位置如图所示,则下列结论中错误的是( )
A.1 B.-5 C.-5或-1 D.5或1
4.若│x│= 3,│y│= 2,且x>y,则x+y的值为( )
C
D
(1)(-0.6)+(-2.7); (2)3.7+(-8.4);
(3)3.22+1.78; (4)7+(-3.3).
5.计算
答案:(1)-3.3 (2)-4.7 (3)5 (4)3.7
解:中午的气温为-25+11=-14(℃),
夜间的气温为-14+(-13)=-27(℃)
6.某城市一天早晨的气温是-25℃,中午上升了11℃,夜间又下降了13℃,那么这天中午、夜间的气温分别是多少?
课堂总结
确定类型 定符号 绝对值
同号
异号(绝对值不相等)
异号(互为相反数) 与0相加 相同符号
取绝对值较大的加数的符号
相加
相减
结果是0
仍是这个数
有理数的加法法则:
