22.2 二次函数与一元二次方程课件(共31张PPT) 人教版数学九年级上册
文档属性
| 名称 | 22.2 二次函数与一元二次方程课件(共31张PPT) 人教版数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 00:00:00 | ||
图片预览





文档简介
(共31张PPT)
22.2 二次函数与一元二次方程
2023—2024学年人教版数学九年级上册
1.关于 x 的一元一次方程 kx+b=0 的解为 x=1,则当 x=___时,一次函数 y=kx+b 的函数值为 0.
1
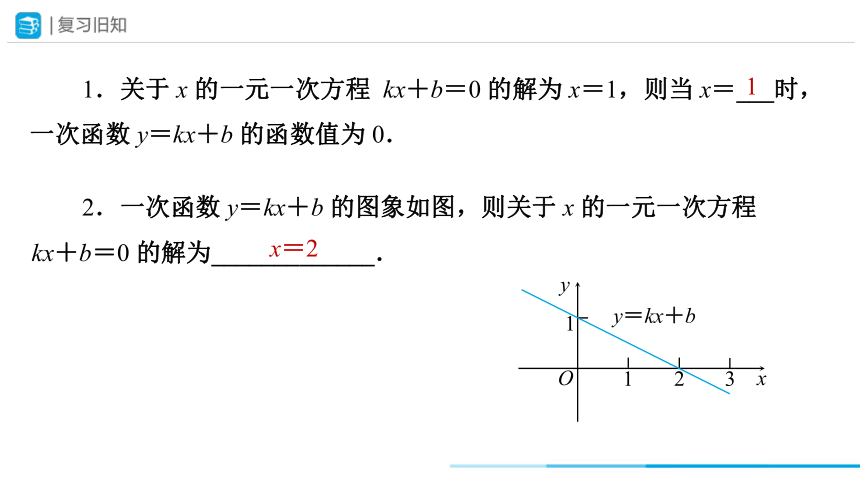
2.一次函数 y=kx+b 的图象如图,则关于 x 的一元一次方程 kx+b=0 的解为_____________.
x=2
O
y
1
3
2
x
y=kx+b
1
3.一次函数与一元一次方程之间的关系.
一次函数与
一元一次方程
数:在函数 y=ax+b(a≠0)中,当 y=0 时, x 的值 一元一次方程 ax+b=0 的解
形:函数 y=ax+b(a≠0)的图象与 x 轴的交点的横坐标 一元一次方程 ax+b=0 的解
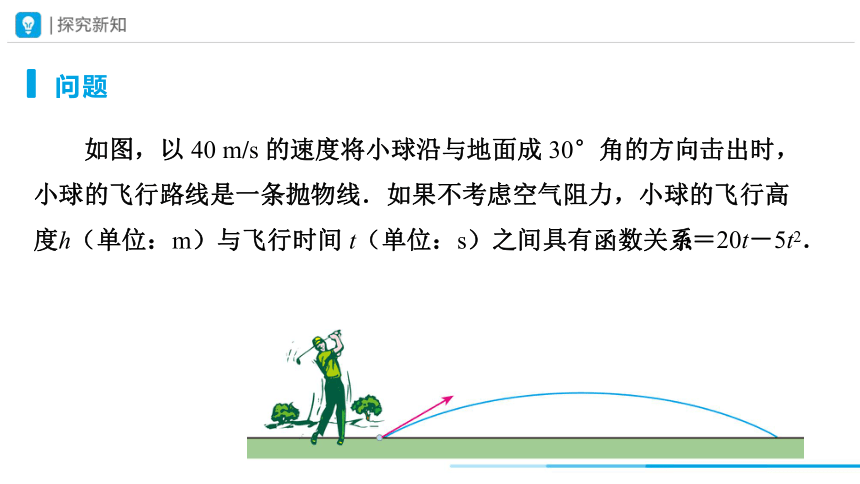
问题
如图,以 40 m/s 的速度将小球沿与地面成 30°角的方向击出时,小球的飞行路线是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间 t(单位:s)之间具有函数关系
h=20t-5t2.
考虑以下问题:
(1)小球的飞行高度能否达到 15 m?如果能,需要飞行多少时间?
(2)小球的飞行高度能否达到 20 m?如果能,需要飞行多少时间?
(3)小球的飞行高度能否达到 20.5 m?为什么?
(4)小球从飞出到落地要用多少时间?
分析:由于小球的飞行高度 h 与飞行时间 t 有函数关系 h=20t-5t2,所以可以将问题中 h 的值代入函数解析式,得到关于 t 的一元二次方程.如果方程有合乎实际的解,则说明小球的飞行高度可以达到问题中h 的值;否则,说明小球的飞行高度不能达到问题中 h 的值.
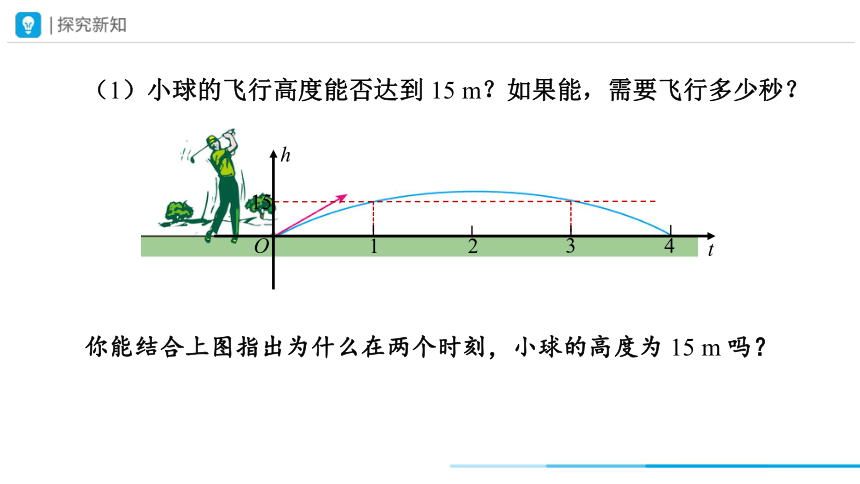
(1)小球的飞行高度能否达到 15 m?如果能,需要飞行多少秒?
当小球飞行 1 s 和 3 s 时,它的飞行高度为 15 m.
解:(1)解方程 15=20t-5t2,
t2-4t+3=0,t1=1,t2=3.
(1)小球的飞行高度能否达到 15 m?如果能,需要飞行多少秒?
你能结合上图指出为什么在两个时刻,小球的高度为 15 m 吗?
O
h
t
1
3
2
4
15
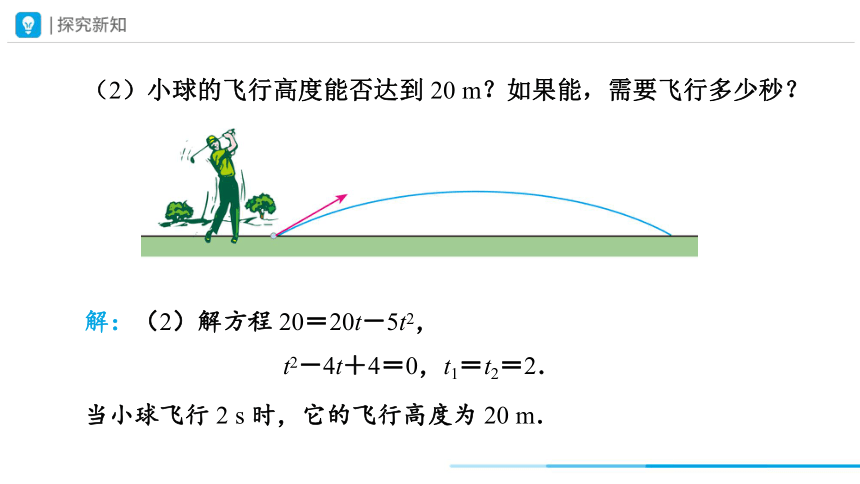
(2)小球的飞行高度能否达到 20 m?如果能,需要飞行多少秒?
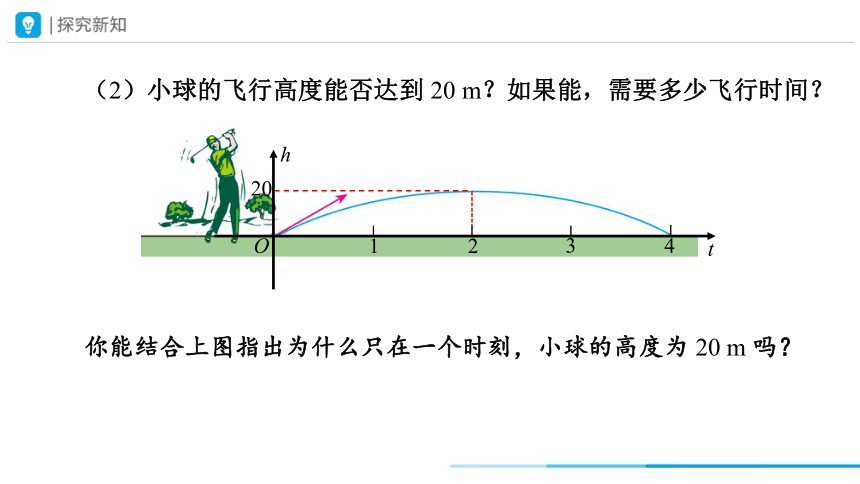
当小球飞行 2 s 时,它的飞行高度为 20 m.
解:(2)解方程 20=20t-5t2,
t2-4t+4=0,t1=t2=2.
1
3
2
4
O
h
t
20
(2)小球的飞行高度能否达到 20 m?如果能,需要多少飞行时间?
你能结合上图指出为什么只在一个时刻,小球的高度为 20 m 吗?
(3)小球的飞行高度能否达到 20.5 m?为什么?
因为(-4)2-4×4.1<0,所以方程无实数根.这就是说,小球的飞行高度达不到 20.5 m.
解:(3)解方程 20.5=20t-5t2,
t2-4t+4.1=0.
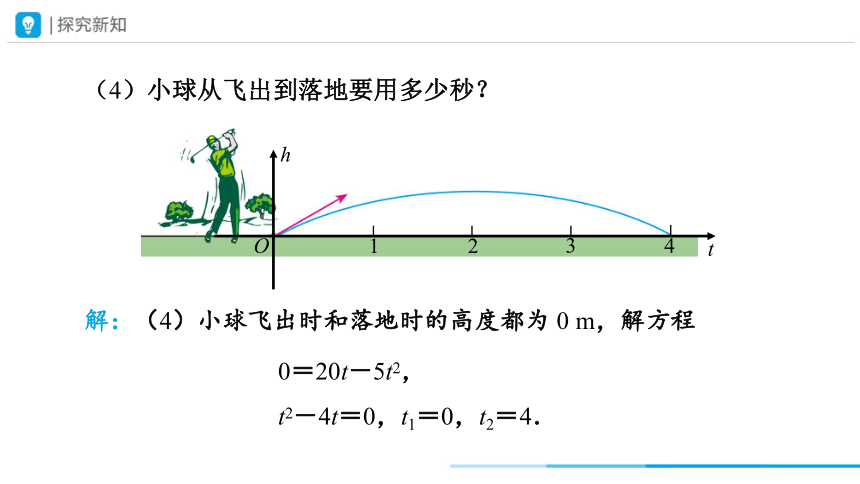
(4)小球从飞出到落地要用多少秒?
解:(4)小球飞出时和落地时的高度都为 0 m,解方程
0=20t-5t2,
t2-4t=0,t1=0,t2=4.
1
3
2
4
O
h
t
当小球飞行 0 s 和 4 s 时,它的高度为 0 m,这表明小球从飞出到落地要用 4 s.从图来看,0 s 时小球从地面飞出,4 s 时小球落回地面.
(4)小球从飞出到落地要用多少时间?
1
3
2
4
O
h
t
归纳
从上面可以看出,二次函数与一元二次方程关系密切.例如,已知二次函数 y=-x2+4x 的值为 3,求自变量 x 的值,可以看作解一元二次方程 -x2+4x=3(即x2-4x+3=0).反过来,解方程 -x2+4x+3=0 又可以看作已知二次函数 y=-x2+4x +3的值为 0,求自变量 x 的值.
思考
下列二次函数的图象与 x 轴有公共点吗?如果有,公共点的横坐标是多少?当 x 取公共点的横坐标时,函数值是多少?由此,你能得出相应的一元二次方程的根吗?
(1)y=x +x-2;(2)y=x -6x+9;(3)y=x -x+1.
在同一直角坐标系中,画出这些函数的图象(如图).
抛物线 y=x2+x-2 与 x 轴有两个公共点,它们的横坐标是-2,1.
当 x 取公共点的横坐标时,函数值是 0.由此得出方程 x2+x-2=0 的根是-2,1.
在同一直角坐标系中,画出这些函数的图象(如图).
抛物线 y=x2-6x+9 与 x 轴有一个公共点,这点的横坐标是 3.
当 x=3 时,函数值是 0.由此得出方程 x2-6x+9=0 有两个相等的实数根 3.
在同一直角坐标系中,画出这些函数的图象(如图).
抛物线 y=x2-x+1 与 x 轴没有公共点.由此可知,方程 x2-x+1=0 没有实数根.
反过来,由一元二次方程的根的情况,也可以确定相应的二次函数的图象与 x 轴的位置关系.
观看动图,思考二次函数图象与 x 轴的公共点与一元二次方程根之间的关系.
观看动图,思考二次函数图象与 x 轴的公共点与一元二次方程根之间的关系.
归纳
一般地,从二次函数 y=ax2+bx+c 的图象可得如下结论.
(1)如果抛物线 y=ax2+bx十c 与 x 轴有公共点,公共点的横坐标是 x0,那么当 x=x0 时,函数值是 0,因此 x=x0 是方程 ax2+bx+c=0 的一个根.
归纳
一般地,从二次函数 y=ax2+bx+c 的图象可得如下结论.
(2)二次函数 y=ax2+bx+c 的图象与 x 轴的位置关系有三种:没有公共点,有一个公共点,有两个公共点.这对应着一元二次方程 ax2+bx+c=0 的根的三种情况:没有实数根,有两个相等的实数根,有两个不等的实数根.
例 利用函数图象求方程 x2-2x-2=0 的实数根(结果保留小数点后一位).
解:方法 1:画出函数 y=x2-2x-2 的图象(如图),它与 x 轴的
公共点的横坐标大约是-0.7,2.7.
所以方程 x2-2x-2=0 的实数根为x1≈-0.7,x2≈2.7.
方法 2:我们还可以通过不断缩小根所在的范围估计一元二次方程的根.
当自变量 x=2 时,y<0,当自变量 x=3 时,y>0,即方程 x2-2x-2=0 在 2,3 之间有根.
取 2,3 的平均数 2.5,当自变量 x=2.5 时,y<0,即方程 x2-2x-2=0 在 2.5,3 之间有根.
取 2.5,3 的平均数 2.75,当自变量 x=2.75 时,y>0,即方程 x2-2x-2=0 在 2.5,2.75 之间有根.
取 2.5,2.75 的平均数 2.625,当自变量 x=2.625 时,y<0,即方程 x2-2x-2=0 在 2.625,2.75 之间有根.
重复上述步骤,我们逐步得到:这个根在 2.687 5,2.75 之间……可以看到:根所在的范围越来越小,根所在范围的两端的值越来越接近根的值,因而可以作为根的近似值.
当要求根的近似值与根的准确值的差的绝对值小于 0.1 时,由于|2.687 5-2.75|=0.062 5<0.1,我们可以将 2.687 5 作为根的近似值.
你能用这种方法得出方程 x2-2x-2=0 的另一个根的近似值吗(要求根的近似值与根的准确值的差的绝对值小于 0.1)?
当自变量 x=-1 时,y>0,当自变量 x=0 时,y<0,即方程 x2-2x-2=0 在-1,0 之间有根.
取-1,0 的平均数-0.5,当自变量 x=-0.5 时,y<0,即方程 x2-2x-2=0 在-0.5,-1 之间有根.
通过取平均数的方法不断缩小根所在的范围.由于|-0.75-(-0.687 5)|=0.062 5<0.1,我们可以将 -0.687 5 作为另一个根的近似值.
利用二次函数图象求一元二次方程的近似根的步骤:
(1)画出函数 y=ax2+bx+c(a≠0)的图象;
(2)确定抛物线与 x 轴的交点的个数,看交点的横坐标在哪两个数之间;
(3)列表,根据题目实际情况在两个数之间合理等分,并用计算器算出每个等分点所对应的函数值 y,近似根在对应 y 值正负交换的地方;
(4)根据精度要求写出方程根的近似值.
二次函数与一元二次方程
二次函数与一元二次方程之间的转化
利用二次函数图象求一元二次方程的近似根
抛物线与 x 轴的位置关系与一元二次方程根的情况
谢谢
22.2 二次函数与一元二次方程
2023—2024学年人教版数学九年级上册
1.关于 x 的一元一次方程 kx+b=0 的解为 x=1,则当 x=___时,一次函数 y=kx+b 的函数值为 0.
1
2.一次函数 y=kx+b 的图象如图,则关于 x 的一元一次方程 kx+b=0 的解为_____________.
x=2
O
y
1
3
2
x
y=kx+b
1
3.一次函数与一元一次方程之间的关系.
一次函数与
一元一次方程
数:在函数 y=ax+b(a≠0)中,当 y=0 时, x 的值 一元一次方程 ax+b=0 的解
形:函数 y=ax+b(a≠0)的图象与 x 轴的交点的横坐标 一元一次方程 ax+b=0 的解
问题
如图,以 40 m/s 的速度将小球沿与地面成 30°角的方向击出时,小球的飞行路线是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间 t(单位:s)之间具有函数关系
h=20t-5t2.
考虑以下问题:
(1)小球的飞行高度能否达到 15 m?如果能,需要飞行多少时间?
(2)小球的飞行高度能否达到 20 m?如果能,需要飞行多少时间?
(3)小球的飞行高度能否达到 20.5 m?为什么?
(4)小球从飞出到落地要用多少时间?
分析:由于小球的飞行高度 h 与飞行时间 t 有函数关系 h=20t-5t2,所以可以将问题中 h 的值代入函数解析式,得到关于 t 的一元二次方程.如果方程有合乎实际的解,则说明小球的飞行高度可以达到问题中h 的值;否则,说明小球的飞行高度不能达到问题中 h 的值.
(1)小球的飞行高度能否达到 15 m?如果能,需要飞行多少秒?
当小球飞行 1 s 和 3 s 时,它的飞行高度为 15 m.
解:(1)解方程 15=20t-5t2,
t2-4t+3=0,t1=1,t2=3.
(1)小球的飞行高度能否达到 15 m?如果能,需要飞行多少秒?
你能结合上图指出为什么在两个时刻,小球的高度为 15 m 吗?
O
h
t
1
3
2
4
15
(2)小球的飞行高度能否达到 20 m?如果能,需要飞行多少秒?
当小球飞行 2 s 时,它的飞行高度为 20 m.
解:(2)解方程 20=20t-5t2,
t2-4t+4=0,t1=t2=2.
1
3
2
4
O
h
t
20
(2)小球的飞行高度能否达到 20 m?如果能,需要多少飞行时间?
你能结合上图指出为什么只在一个时刻,小球的高度为 20 m 吗?
(3)小球的飞行高度能否达到 20.5 m?为什么?
因为(-4)2-4×4.1<0,所以方程无实数根.这就是说,小球的飞行高度达不到 20.5 m.
解:(3)解方程 20.5=20t-5t2,
t2-4t+4.1=0.
(4)小球从飞出到落地要用多少秒?
解:(4)小球飞出时和落地时的高度都为 0 m,解方程
0=20t-5t2,
t2-4t=0,t1=0,t2=4.
1
3
2
4
O
h
t
当小球飞行 0 s 和 4 s 时,它的高度为 0 m,这表明小球从飞出到落地要用 4 s.从图来看,0 s 时小球从地面飞出,4 s 时小球落回地面.
(4)小球从飞出到落地要用多少时间?
1
3
2
4
O
h
t
归纳
从上面可以看出,二次函数与一元二次方程关系密切.例如,已知二次函数 y=-x2+4x 的值为 3,求自变量 x 的值,可以看作解一元二次方程 -x2+4x=3(即x2-4x+3=0).反过来,解方程 -x2+4x+3=0 又可以看作已知二次函数 y=-x2+4x +3的值为 0,求自变量 x 的值.
思考
下列二次函数的图象与 x 轴有公共点吗?如果有,公共点的横坐标是多少?当 x 取公共点的横坐标时,函数值是多少?由此,你能得出相应的一元二次方程的根吗?
(1)y=x +x-2;(2)y=x -6x+9;(3)y=x -x+1.
在同一直角坐标系中,画出这些函数的图象(如图).
抛物线 y=x2+x-2 与 x 轴有两个公共点,它们的横坐标是-2,1.
当 x 取公共点的横坐标时,函数值是 0.由此得出方程 x2+x-2=0 的根是-2,1.
在同一直角坐标系中,画出这些函数的图象(如图).
抛物线 y=x2-6x+9 与 x 轴有一个公共点,这点的横坐标是 3.
当 x=3 时,函数值是 0.由此得出方程 x2-6x+9=0 有两个相等的实数根 3.
在同一直角坐标系中,画出这些函数的图象(如图).
抛物线 y=x2-x+1 与 x 轴没有公共点.由此可知,方程 x2-x+1=0 没有实数根.
反过来,由一元二次方程的根的情况,也可以确定相应的二次函数的图象与 x 轴的位置关系.
观看动图,思考二次函数图象与 x 轴的公共点与一元二次方程根之间的关系.
观看动图,思考二次函数图象与 x 轴的公共点与一元二次方程根之间的关系.
归纳
一般地,从二次函数 y=ax2+bx+c 的图象可得如下结论.
(1)如果抛物线 y=ax2+bx十c 与 x 轴有公共点,公共点的横坐标是 x0,那么当 x=x0 时,函数值是 0,因此 x=x0 是方程 ax2+bx+c=0 的一个根.
归纳
一般地,从二次函数 y=ax2+bx+c 的图象可得如下结论.
(2)二次函数 y=ax2+bx+c 的图象与 x 轴的位置关系有三种:没有公共点,有一个公共点,有两个公共点.这对应着一元二次方程 ax2+bx+c=0 的根的三种情况:没有实数根,有两个相等的实数根,有两个不等的实数根.
例 利用函数图象求方程 x2-2x-2=0 的实数根(结果保留小数点后一位).
解:方法 1:画出函数 y=x2-2x-2 的图象(如图),它与 x 轴的
公共点的横坐标大约是-0.7,2.7.
所以方程 x2-2x-2=0 的实数根为x1≈-0.7,x2≈2.7.
方法 2:我们还可以通过不断缩小根所在的范围估计一元二次方程的根.
当自变量 x=2 时,y<0,当自变量 x=3 时,y>0,即方程 x2-2x-2=0 在 2,3 之间有根.
取 2,3 的平均数 2.5,当自变量 x=2.5 时,y<0,即方程 x2-2x-2=0 在 2.5,3 之间有根.
取 2.5,3 的平均数 2.75,当自变量 x=2.75 时,y>0,即方程 x2-2x-2=0 在 2.5,2.75 之间有根.
取 2.5,2.75 的平均数 2.625,当自变量 x=2.625 时,y<0,即方程 x2-2x-2=0 在 2.625,2.75 之间有根.
重复上述步骤,我们逐步得到:这个根在 2.687 5,2.75 之间……可以看到:根所在的范围越来越小,根所在范围的两端的值越来越接近根的值,因而可以作为根的近似值.
当要求根的近似值与根的准确值的差的绝对值小于 0.1 时,由于|2.687 5-2.75|=0.062 5<0.1,我们可以将 2.687 5 作为根的近似值.
你能用这种方法得出方程 x2-2x-2=0 的另一个根的近似值吗(要求根的近似值与根的准确值的差的绝对值小于 0.1)?
当自变量 x=-1 时,y>0,当自变量 x=0 时,y<0,即方程 x2-2x-2=0 在-1,0 之间有根.
取-1,0 的平均数-0.5,当自变量 x=-0.5 时,y<0,即方程 x2-2x-2=0 在-0.5,-1 之间有根.
通过取平均数的方法不断缩小根所在的范围.由于|-0.75-(-0.687 5)|=0.062 5<0.1,我们可以将 -0.687 5 作为另一个根的近似值.
利用二次函数图象求一元二次方程的近似根的步骤:
(1)画出函数 y=ax2+bx+c(a≠0)的图象;
(2)确定抛物线与 x 轴的交点的个数,看交点的横坐标在哪两个数之间;
(3)列表,根据题目实际情况在两个数之间合理等分,并用计算器算出每个等分点所对应的函数值 y,近似根在对应 y 值正负交换的地方;
(4)根据精度要求写出方程根的近似值.
二次函数与一元二次方程
二次函数与一元二次方程之间的转化
利用二次函数图象求一元二次方程的近似根
抛物线与 x 轴的位置关系与一元二次方程根的情况
谢谢
同课章节目录
