第十三章 轴对称 章末复习课件(共39张PPT) 人教版八年级数学上册
文档属性
| 名称 | 第十三章 轴对称 章末复习课件(共39张PPT) 人教版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 506.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 14:38:34 | ||
图片预览


文档简介
(共39张PPT)
《轴对称》
章末复习
知识梳理
1
轴对称图形
轴对称图形概念
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形。
1
轴对称图形
两个图形成轴对称概念
把一个图形沿某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称。
1
轴对称图形
性质
①不管是轴对称图形还是两个图形关于某条直线对称,对称轴都是任何一对对应点所连线段的___________.
②对称的图形都______.
垂直平分线
全等
2
线段的垂直平分线
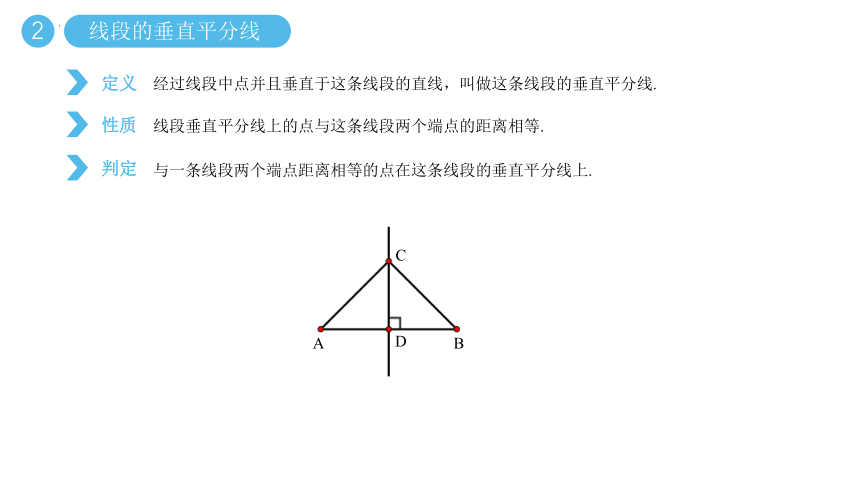
定义
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
性质
判定
线段垂直平分线上的点与这条线段两个端点的距离相等.
与一条线段两个端点距离相等的点在这条线段的垂直平分线上.
A
B
C
D
3
等腰三角形
概念
有两条边相等的三角形叫做等腰三角形.相等的两条边叫做腰,另一条边叫做底边,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角。
A
B
C
3
等腰三角形
性质
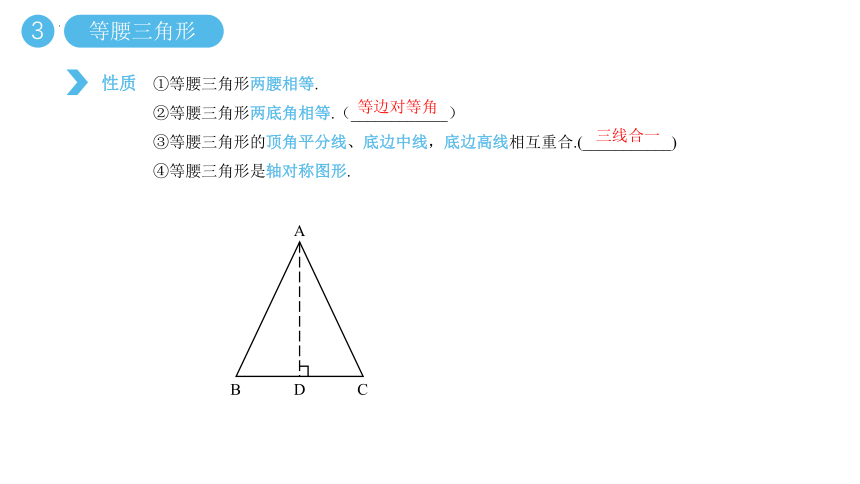
①等腰三角形两腰相等.
②等腰三角形两底角相等.(____________)
③等腰三角形的顶角平分线、底边中线,底边高线相互重合.(___________)
④等腰三角形是轴对称图形.
A
B
C
D
等边对等角
三线合一
3
等腰三角形
判定
①有两条边相等的三角形是等腰三角形. (定义)
②如果一个三角形有两个角相等,那么这两个角所对的边也相等.(___________)
A
B
C
等角对等边
4
等边三角形
定义
三条边都相等的三角形叫做等边三角形。
A
B
C
4
等边三角形
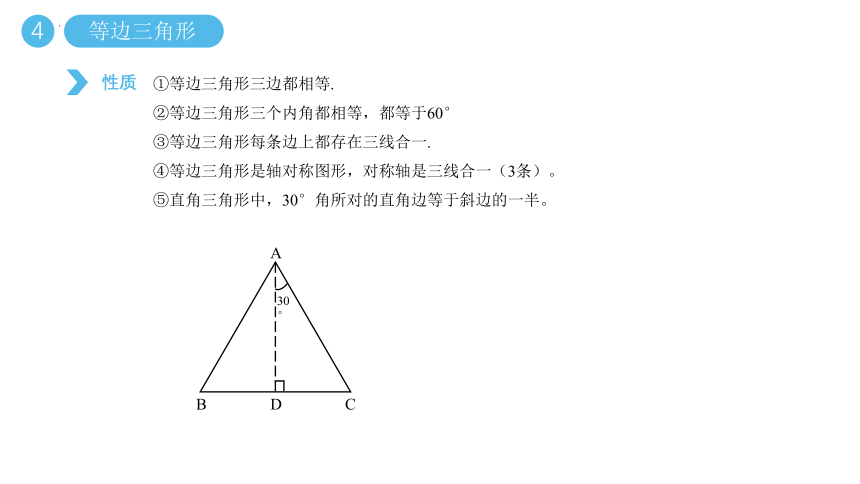
性质
①等边三角形三边都相等.
②等边三角形三个内角都相等,都等于60°
③等边三角形每条边上都存在三线合一.
④等边三角形是轴对称图形,对称轴是三线合一(3条)。
⑤直角三角形中,30°角所对的直角边等于斜边的一半。
A
B
C
D
30°
4
等边三角形
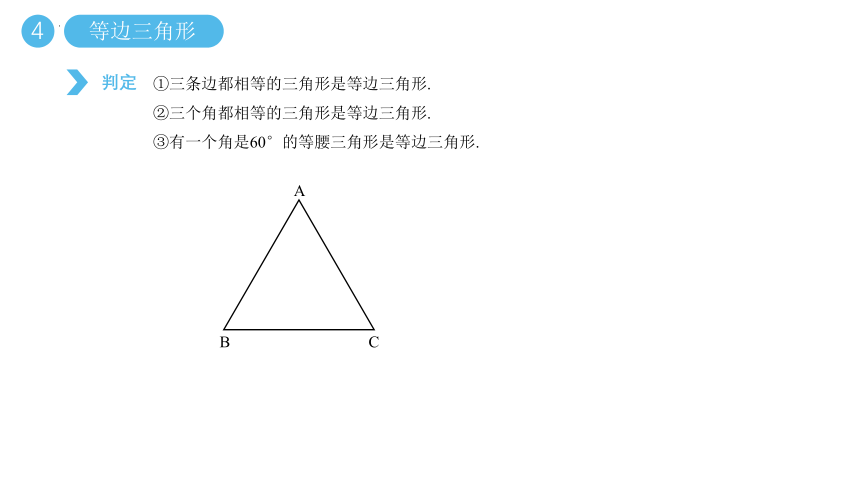
判定
①三条边都相等的三角形是等边三角形.
②三个角都相等的三角形是等边三角形.
③有一个角是60°的等腰三角形是等边三角形.
A
B
C
5
平面直角坐标系中的轴对称变换
关于坐标轴对称的点的坐标性质
P(x,y)
①点P(x,y)关于x轴对称的点的坐标为P1(x,-y)
②点P(x,y)关于y轴对称的点的坐标为P2(-x,y)
P1(x,-y)
P2(-x,y)
5
平面直角坐标系中的轴对称变换
关于坐标轴夹角平分线对称
①点P(x,y)关于第一、三象限坐标轴夹角平分线y=x对称的点的坐标是P 1(y,x)
②点P(x,y)关于第二、四象限坐标轴夹角平分线y=-x对称的点的坐标是P 2(-y,-x)
y=x
y=-x
P(x,y)
P 1(y,x)
P 2(-y,-x)
5
平面直角坐标系中的轴对称变换
关于平行于坐标轴的直线对称
①点P(x,y)关于直线x=m对称的点的坐标是P 1 (2m-x,y)
②点P(x,y)关于直线y=n对称的点的坐标是P 2 (x,2n-y)
x=m
y=n
P(x,y)
P 1 (2m-x,y)
P2
(x,2n-y)
典型例题
方 程
例题1 下列交通指示标识中,是轴对称图形的有 ( )
题型一
轴对称及轴对称图形
A. 1个 B. 2个 C. 3个 D. 4个
C
方 程
例题2 如图,每个小正方形的面积是1.
(1)作出△ABC关于直线成轴对称的图形△A′B′C′.
(2)求出△ABC的面积.
题型一
轴对称及轴对称图形
答案:(1)如图,△A′B′C′就是所求作的图形。
方 程
例题2 如图,每个小正方形的面积是1.
(1)作出△ABC关于直线成轴对称的图形△A′B′C′.
(2)求出△ABC的面积.
题型一
轴对称及轴对称图形
答案:(2)如图所示,
S△ABC=S正方形DBFE-S△ADB-S△BCF-S△AEC
=4×4- ×1×4- ×1×4- ×3×3
=7.5
答:△ABC的面积为7.5
方 程
例题1 如图,在4×4正方形网格中,将图中的2个小正方形涂上阴影,若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形是轴对称图形,那么符合条件的小正方形共有( )
题型二
设计轴对称图形
A.7个 B.8个 C.9个 D.10个
D
方 程
例题2 请在如图四个3×3 的正方形网格中,画出与格点三角形(阴影部分)成轴对称且以格点为顶点的三角形,并将所画三角形涂上阴影。(注:所画的四个图不能重复)
题型二
设计轴对称图形
方 程
例题1 如下图,已知:在△ABC中,∠BAC=90°。BE平分∠ABC,DE⊥BC于D.
证明:BE垂直平分AD.
题型三
线段的垂直平分线的性质及判定
证明:连接AD交BE于点F
∵BE平分∠ABC
∴∠ABE=∠CBE
∵DE⊥BC
∴∠BDE=∠BAC=90°
又∵BE=BE
∴△BAE≌△BDE
∴BA=BD
在△ABF和△DBF中
∵BA=BD,∠ABE=∠CBE,BF=BF
∴△ABF≌△DBF
∴∠BFA=∠BFD AF=EF
又∵∠BFA+∠BFD=180°
∴∠BFA=∠BFD= ×180°= 90°
∴BE垂直平分AD
方 程
例题2 已知:如图,点P为∠AOB内一点,分别作出P点关于OB、OA的对称点P1,P2,连接P1P2交OB于M,交OA于N,P1P2=15,则△PMN的周长为__________。
题型三
线段的垂直平分线的性质及判定
解析:连接PP1,PP2
∵点P与点P1,P2分别关于OB、OA对称
∴OB、OA分别是PP1,PP2的垂直平分线,
∴PM=MP1,PN=NP2
∴△PMN的周长=PM+PN+MN= MP1+NP2+MN= P1P2=15
方 程
例题3 如图, △ABC中, AD平分∠BAC , DG⊥BC且平分BC, DE⊥AB于E , DF⊥AC于F.
(1)说明BE=CF的理由;
(2)如果AB=5,AC=3,求AE、BE的长.
题型三
线段的垂直平分线的性质及判定
(1) 证明:连接 BD,CD
∵AD 平分∠BAC,DE⊥AB,DF⊥AC.
∴DE=DF,∠BED=∠CFD=90°,
∵DG⊥BC 且平分 BC,
∴BD=CD,
在 Rt△BED与Rt△CFD 中
∴Rt△BED≌Rt△CFD (HL)
∴BE=CF
方 程
例题3 如图, △ABC中, AD平分∠BAC , DG⊥BC且平分BC, DE⊥AB于E , DF⊥AC于F.
(1)说明BE=CF的理由;
(2)如果AB=5,AC=3,求AE、BE的长.
题型三
线段的垂直平分线的性质及判定
(2)解:在△AED和△AFD中
∴△AED≌△AFD (AAS),
∴AE=AF,
设 BE=x,则 CF=x,
∵AB=5,AC=3,AE=AB - BE,AF=AC+CF
∴5-x=3+x,
解得: x =1,
∴BE=1,AE=AB-BE=5-1=4.
方 程
例题1 已知P(3,2a-5)与Q(3,a+2)关于x轴对称,则a=________。
题型四
用坐标表示轴对称
解析:因为 P,Q关于x轴对称,我们知道点P(x,y)关于x轴对称的点的坐标是(x,-y)
所以2a-5=-( a+2),
解得a=1。
答案:1
方 程
例题1 如图所示,△ABC是等腰直角三角形,∠BAC=90°,AB=AC.
(1)若D为BC的中点,过D作DM⊥DN分别交AB、AC于M、N,
求证:DM=DN;
题型五
等腰三角形的性质与判定
解:(1) 连接AD,
∵D为BC中点,AB=AC,∠BAC=90°
∴AD=BD,∠BAD=∠C,
∴AD=BD=DC,
∵∠ADM+∠ADN=90°,∠ADN+∠CDN=90°
∴∠ADM=∠CDN,
在△AMD和△CND 中
∴△AMD≌△CND (ASA)
∴DM=DN.
方 程
例题1 如图所示,△ABC是等腰直角三角形,∠BAC=90°,AB=AC.
(2)若D为BC的中点,DM⊥DN分别和BA、AC延长线交于M、N,问DM和DN有何数量关系,并证明.
题型五
等腰三角形的性质与判定
(2) 连接AD,
∵D为BC中点
∴AD=BD,∠BAD=∠C
∵∠ADM+∠MDC=90°,∠MDC+∠CDN=90°
∴∠ADM=∠CDN,
∵∠MAD=∠MAC+∠DAC=135°,
∠NCD=180°-∠ACD=135°
在△AMD和△CND 中
∴△AMD≌△CND (ASA)
∴DM=DN.
方 程
例题2 (1)如图①,△ABC中,∠ABC、∠ACB的平分线交于O点,过O点作EF//BC交AB、AC于点E、F,试猜想EF、BE、CF之间有怎样的关系,并说明理由;
题型五
等腰三角形的性质与判定
解:(1) EF=BE+CF
理由:∵BO平分∠ABC,CO平分∠ACB
∴∠EBO=∠OBC,∠FCO=∠OCB
∵EF∥BC
∴∠EOB=∠OBC, ∠FOC=∠OCB
∴∠EBO=∠EOB,∠FOC=∠FCO
∴BE=OE,CF=OF
∴EF=OE+OF=BE+CF
方 程
例题2 (2)如图,若将图①中∠ACB 的平分线改为外角∠ACD 的平分线,其它条件不变,请直接写出 EF、BE、CF之间的关系.
题型五
等腰三角形的性质与判定
(2) 不成立
理由:∵BO平分∠ABC,CO平分∠ACD
∴∠EBO=∠OBC,∠FCO=∠OCD
∵EF//BC,
∴∠EOB=∠OBC,∠FOC=∠OCD
∴∠EBO=∠EOB,∠FOC=∠FCO
∴BE=OE,CF=OF,
∴EF=OE-OF=BE-CF
故答案为 EF=BE-CF
方 程
例题1 如图,△ABC是等边三角形,DE//AB分别交BC、AC于点D、E.过点E作EF⊥DE,交线段 BC的延长线于点F.
(1)求证:CE=CF;
题型六
等边三角形的性质与判定
解:(1) ∵△ABC是等边三角形
∴AB=AC=BC,∠BAC=∠ABC=∠ACB=60°
∵AE=BD
∴AC-AE=BC-BD
∴CE=CD,且∠ACB=60°
∴△CDE是等边三角形
∴∠ECD=∠DEC=60°
∵EF⊥DE
∴∠DEF=90°
∴∠CEF=30°
∵∠DCE=∠CEF+∠CFE=60°
∴∠CEF=∠CFE=30°
∴CE=CF
方 程
例题1 如图,△ABC是等边三角形,DE//AB分别交BC、AC于点D、E.过点E作EF⊥DE,交线段 BC的延长线于点F.
(2)若BD= CE,AB=8,求线段DF的长.
题型六
等边三角形的性质与判定
(2)∵BD= CE,CE=CD
∴BD= CD
∵AB=8
∴BC=8
∴BD=2,CD=6
∵CE=CF=CD
∴CF=6
∴DF=DC+CF=12
方 程
例题2 如图,C为线段AE 上一动点,(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.
求证:(1)AD=BE
题型六
等边三角形的性质与判定
证明: (1) ∵△ABC和△CDE 是正三角形
∴AC=BC,CD=CE,∠ACB=∠DCE=60°
∵∠ACD=∠ACB+∠BCD,∠BCE=∠DCE+∠BCD
∴∠ACD=∠BCE
∴△ADC≌△BEC (SAS)
∴AD=BE
方 程
例题2 如图,C为线段AE 上一动点,(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.
求证:(2) △APC≌△BOC
题型六
等边三角形的性质与判定
(2) ∵△ADC≌△BEC
∴∠ACP=∠BCQ,AC=BC,∠CAP=∠CBQ
∴△APC≌△BQC(ASA)
方 程
例题2 如图,C为线段AE 上一动点,(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.
求证:(3) △PCQ是等边三角形
题型六
等边三角形的性质与判定
(3) ∵CD=CE,∠DCP=∠ECQ=60°,∠ADC=∠BEC
∴△CDP≌△CEQ(ASA).
∴CP=CQ,
∴∠CPQ=∠CQP=60°
∴△CPQ是等边三角形
方 程
例题1 (1) 问题发现
如图1,△ACB和△DCE 均为等边三角形,点A、D、E在同一直线上,连接BE,求∠AEB的度数
题型七
手拉手模型
解:(1) ∵△ACB 和△DCE 均为等边三角形
∴CA=CB,CD=CE,∠ACB=∠DCE=60°
∴∠ACD=60°-∠CDB=∠BCE.
在△ACD和△BCE 中
∴△ACD≌△BCE (SAS)
∴∠ADC=∠BEC
∵△DCE 为等边三角形
∴∠CDE=∠CED=60°
∵点A,D,E在同一直线上,
∴∠ADC=120°
∴∠BEC=120°
∴∠AEB=∠BEC-∠CED=60°
方 程
例题1 (2)拓展探究
如图2,△ACB和△DCE 均为等腰直角三角形,∠ACB=∠DCE=90°点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请求∠AEB 的度数及线段 CM、AE、BE之间的数量关系,并说明理由.
题型七
手拉手模型
∴△ACD≌△BCE (SAS)
∴AD=BE,∠ADC=∠BEC
∵△DCE 为等腰直角三角形,
∴∠CDE=∠CED=45°
∵点A,D,E在同一直线上
∴∠ADC=135°
∴∠BEC=135°
∴∠AEB=∠BEC- ∠CED=90°
∵CD=CE,CM⊥DE,
∴DM=ME.
(2) ∠AEB=90°,AE=BE+2CM
理由:∵△ACB 和△DCE 均为等腰直角三角形
∴CA=CB,CD=CE,∠ACB=∠DCE=90°
∴∠ACD=∠BCE
∵∠DCE=90°,
∴DM=ME=CM
∴AE=AD+DE=BE+2CM
在△ACD和△BCE中,
方 程
例题1 如图,∠AOB=30°,点M、N分别是射线 OB、OA上的动点,点P为∠AOB内一点,且OP=4,则△PMN的周长的最小值为 ( )
题型八
轴对称最短路径问题
A.2 B.4 C.6 D.8
解: 分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M'、N',连接OC、OD、PM'、PN’
∵点P关于 OA 的对称点为 C,
∴PM'=CM',OP=OC,∠COB=∠POB
∵点P关于 OB的对称点为 D
∴PN'=DN',OP=OD,∠DOA= ∠POA,
∴OC=OD=OP=4,∠COD=∠COB+∠POB+∠POA+∠DOA
=2∠POA+2∠POB=2∠AOB=60°.
∴△COD 是等边三角形,
∴CD=OC=OD=4.
∴当M、N分别与M'、N'重合时,
△PMN的周长的最小值=PM'+M'N'+PN'=DN'+M'N'+CM'=CD=4
故选:B.
方 程
例题2 如图,在四边形ABCD中,∠A=∠C=90°,∠B=34°,在边AB、BC分别找一点E、F使△DEF的周长最小,此时∠EDF=_________.
题型八
轴对称最短路径问题
解: 如图,作点D关于BA的对称点P,点D关于BC的对称点Q,连接PQ,交AB于E',交BC于 F',则点 E',F'即为所求.
∵四边形ABCD中,∠A=∠C=90°,∠B=α
∴∠ADC=180°- α,
由轴对称知,△ADE'=△P,△CDF'=∠Q
在△PDQ中,△P+Q=180°- △ADC
=180°- (180° - 34°)
=34°
∴∠ADE'+∠CDF'=∠P+∠Q=34°,
∴∠E'DF'=∠ADC- (∠ADE'+∠CDF')
=180°- 68°
=112°
故答案为: 112°
《轴对称》
章末复习
知识梳理
1
轴对称图形
轴对称图形概念
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形。
1
轴对称图形
两个图形成轴对称概念
把一个图形沿某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称。
1
轴对称图形
性质
①不管是轴对称图形还是两个图形关于某条直线对称,对称轴都是任何一对对应点所连线段的___________.
②对称的图形都______.
垂直平分线
全等
2
线段的垂直平分线
定义
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
性质
判定
线段垂直平分线上的点与这条线段两个端点的距离相等.
与一条线段两个端点距离相等的点在这条线段的垂直平分线上.
A
B
C
D
3
等腰三角形
概念
有两条边相等的三角形叫做等腰三角形.相等的两条边叫做腰,另一条边叫做底边,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角。
A
B
C
3
等腰三角形
性质
①等腰三角形两腰相等.
②等腰三角形两底角相等.(____________)
③等腰三角形的顶角平分线、底边中线,底边高线相互重合.(___________)
④等腰三角形是轴对称图形.
A
B
C
D
等边对等角
三线合一
3
等腰三角形
判定
①有两条边相等的三角形是等腰三角形. (定义)
②如果一个三角形有两个角相等,那么这两个角所对的边也相等.(___________)
A
B
C
等角对等边
4
等边三角形
定义
三条边都相等的三角形叫做等边三角形。
A
B
C
4
等边三角形
性质
①等边三角形三边都相等.
②等边三角形三个内角都相等,都等于60°
③等边三角形每条边上都存在三线合一.
④等边三角形是轴对称图形,对称轴是三线合一(3条)。
⑤直角三角形中,30°角所对的直角边等于斜边的一半。
A
B
C
D
30°
4
等边三角形
判定
①三条边都相等的三角形是等边三角形.
②三个角都相等的三角形是等边三角形.
③有一个角是60°的等腰三角形是等边三角形.
A
B
C
5
平面直角坐标系中的轴对称变换
关于坐标轴对称的点的坐标性质
P(x,y)
①点P(x,y)关于x轴对称的点的坐标为P1(x,-y)
②点P(x,y)关于y轴对称的点的坐标为P2(-x,y)
P1(x,-y)
P2(-x,y)
5
平面直角坐标系中的轴对称变换
关于坐标轴夹角平分线对称
①点P(x,y)关于第一、三象限坐标轴夹角平分线y=x对称的点的坐标是P 1(y,x)
②点P(x,y)关于第二、四象限坐标轴夹角平分线y=-x对称的点的坐标是P 2(-y,-x)
y=x
y=-x
P(x,y)
P 1(y,x)
P 2(-y,-x)
5
平面直角坐标系中的轴对称变换
关于平行于坐标轴的直线对称
①点P(x,y)关于直线x=m对称的点的坐标是P 1 (2m-x,y)
②点P(x,y)关于直线y=n对称的点的坐标是P 2 (x,2n-y)
x=m
y=n
P(x,y)
P 1 (2m-x,y)
P2
(x,2n-y)
典型例题
方 程
例题1 下列交通指示标识中,是轴对称图形的有 ( )
题型一
轴对称及轴对称图形
A. 1个 B. 2个 C. 3个 D. 4个
C
方 程
例题2 如图,每个小正方形的面积是1.
(1)作出△ABC关于直线成轴对称的图形△A′B′C′.
(2)求出△ABC的面积.
题型一
轴对称及轴对称图形
答案:(1)如图,△A′B′C′就是所求作的图形。
方 程
例题2 如图,每个小正方形的面积是1.
(1)作出△ABC关于直线成轴对称的图形△A′B′C′.
(2)求出△ABC的面积.
题型一
轴对称及轴对称图形
答案:(2)如图所示,
S△ABC=S正方形DBFE-S△ADB-S△BCF-S△AEC
=4×4- ×1×4- ×1×4- ×3×3
=7.5
答:△ABC的面积为7.5
方 程
例题1 如图,在4×4正方形网格中,将图中的2个小正方形涂上阴影,若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形是轴对称图形,那么符合条件的小正方形共有( )
题型二
设计轴对称图形
A.7个 B.8个 C.9个 D.10个
D
方 程
例题2 请在如图四个3×3 的正方形网格中,画出与格点三角形(阴影部分)成轴对称且以格点为顶点的三角形,并将所画三角形涂上阴影。(注:所画的四个图不能重复)
题型二
设计轴对称图形
方 程
例题1 如下图,已知:在△ABC中,∠BAC=90°。BE平分∠ABC,DE⊥BC于D.
证明:BE垂直平分AD.
题型三
线段的垂直平分线的性质及判定
证明:连接AD交BE于点F
∵BE平分∠ABC
∴∠ABE=∠CBE
∵DE⊥BC
∴∠BDE=∠BAC=90°
又∵BE=BE
∴△BAE≌△BDE
∴BA=BD
在△ABF和△DBF中
∵BA=BD,∠ABE=∠CBE,BF=BF
∴△ABF≌△DBF
∴∠BFA=∠BFD AF=EF
又∵∠BFA+∠BFD=180°
∴∠BFA=∠BFD= ×180°= 90°
∴BE垂直平分AD
方 程
例题2 已知:如图,点P为∠AOB内一点,分别作出P点关于OB、OA的对称点P1,P2,连接P1P2交OB于M,交OA于N,P1P2=15,则△PMN的周长为__________。
题型三
线段的垂直平分线的性质及判定
解析:连接PP1,PP2
∵点P与点P1,P2分别关于OB、OA对称
∴OB、OA分别是PP1,PP2的垂直平分线,
∴PM=MP1,PN=NP2
∴△PMN的周长=PM+PN+MN= MP1+NP2+MN= P1P2=15
方 程
例题3 如图, △ABC中, AD平分∠BAC , DG⊥BC且平分BC, DE⊥AB于E , DF⊥AC于F.
(1)说明BE=CF的理由;
(2)如果AB=5,AC=3,求AE、BE的长.
题型三
线段的垂直平分线的性质及判定
(1) 证明:连接 BD,CD
∵AD 平分∠BAC,DE⊥AB,DF⊥AC.
∴DE=DF,∠BED=∠CFD=90°,
∵DG⊥BC 且平分 BC,
∴BD=CD,
在 Rt△BED与Rt△CFD 中
∴Rt△BED≌Rt△CFD (HL)
∴BE=CF
方 程
例题3 如图, △ABC中, AD平分∠BAC , DG⊥BC且平分BC, DE⊥AB于E , DF⊥AC于F.
(1)说明BE=CF的理由;
(2)如果AB=5,AC=3,求AE、BE的长.
题型三
线段的垂直平分线的性质及判定
(2)解:在△AED和△AFD中
∴△AED≌△AFD (AAS),
∴AE=AF,
设 BE=x,则 CF=x,
∵AB=5,AC=3,AE=AB - BE,AF=AC+CF
∴5-x=3+x,
解得: x =1,
∴BE=1,AE=AB-BE=5-1=4.
方 程
例题1 已知P(3,2a-5)与Q(3,a+2)关于x轴对称,则a=________。
题型四
用坐标表示轴对称
解析:因为 P,Q关于x轴对称,我们知道点P(x,y)关于x轴对称的点的坐标是(x,-y)
所以2a-5=-( a+2),
解得a=1。
答案:1
方 程
例题1 如图所示,△ABC是等腰直角三角形,∠BAC=90°,AB=AC.
(1)若D为BC的中点,过D作DM⊥DN分别交AB、AC于M、N,
求证:DM=DN;
题型五
等腰三角形的性质与判定
解:(1) 连接AD,
∵D为BC中点,AB=AC,∠BAC=90°
∴AD=BD,∠BAD=∠C,
∴AD=BD=DC,
∵∠ADM+∠ADN=90°,∠ADN+∠CDN=90°
∴∠ADM=∠CDN,
在△AMD和△CND 中
∴△AMD≌△CND (ASA)
∴DM=DN.
方 程
例题1 如图所示,△ABC是等腰直角三角形,∠BAC=90°,AB=AC.
(2)若D为BC的中点,DM⊥DN分别和BA、AC延长线交于M、N,问DM和DN有何数量关系,并证明.
题型五
等腰三角形的性质与判定
(2) 连接AD,
∵D为BC中点
∴AD=BD,∠BAD=∠C
∵∠ADM+∠MDC=90°,∠MDC+∠CDN=90°
∴∠ADM=∠CDN,
∵∠MAD=∠MAC+∠DAC=135°,
∠NCD=180°-∠ACD=135°
在△AMD和△CND 中
∴△AMD≌△CND (ASA)
∴DM=DN.
方 程
例题2 (1)如图①,△ABC中,∠ABC、∠ACB的平分线交于O点,过O点作EF//BC交AB、AC于点E、F,试猜想EF、BE、CF之间有怎样的关系,并说明理由;
题型五
等腰三角形的性质与判定
解:(1) EF=BE+CF
理由:∵BO平分∠ABC,CO平分∠ACB
∴∠EBO=∠OBC,∠FCO=∠OCB
∵EF∥BC
∴∠EOB=∠OBC, ∠FOC=∠OCB
∴∠EBO=∠EOB,∠FOC=∠FCO
∴BE=OE,CF=OF
∴EF=OE+OF=BE+CF
方 程
例题2 (2)如图,若将图①中∠ACB 的平分线改为外角∠ACD 的平分线,其它条件不变,请直接写出 EF、BE、CF之间的关系.
题型五
等腰三角形的性质与判定
(2) 不成立
理由:∵BO平分∠ABC,CO平分∠ACD
∴∠EBO=∠OBC,∠FCO=∠OCD
∵EF//BC,
∴∠EOB=∠OBC,∠FOC=∠OCD
∴∠EBO=∠EOB,∠FOC=∠FCO
∴BE=OE,CF=OF,
∴EF=OE-OF=BE-CF
故答案为 EF=BE-CF
方 程
例题1 如图,△ABC是等边三角形,DE//AB分别交BC、AC于点D、E.过点E作EF⊥DE,交线段 BC的延长线于点F.
(1)求证:CE=CF;
题型六
等边三角形的性质与判定
解:(1) ∵△ABC是等边三角形
∴AB=AC=BC,∠BAC=∠ABC=∠ACB=60°
∵AE=BD
∴AC-AE=BC-BD
∴CE=CD,且∠ACB=60°
∴△CDE是等边三角形
∴∠ECD=∠DEC=60°
∵EF⊥DE
∴∠DEF=90°
∴∠CEF=30°
∵∠DCE=∠CEF+∠CFE=60°
∴∠CEF=∠CFE=30°
∴CE=CF
方 程
例题1 如图,△ABC是等边三角形,DE//AB分别交BC、AC于点D、E.过点E作EF⊥DE,交线段 BC的延长线于点F.
(2)若BD= CE,AB=8,求线段DF的长.
题型六
等边三角形的性质与判定
(2)∵BD= CE,CE=CD
∴BD= CD
∵AB=8
∴BC=8
∴BD=2,CD=6
∵CE=CF=CD
∴CF=6
∴DF=DC+CF=12
方 程
例题2 如图,C为线段AE 上一动点,(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.
求证:(1)AD=BE
题型六
等边三角形的性质与判定
证明: (1) ∵△ABC和△CDE 是正三角形
∴AC=BC,CD=CE,∠ACB=∠DCE=60°
∵∠ACD=∠ACB+∠BCD,∠BCE=∠DCE+∠BCD
∴∠ACD=∠BCE
∴△ADC≌△BEC (SAS)
∴AD=BE
方 程
例题2 如图,C为线段AE 上一动点,(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.
求证:(2) △APC≌△BOC
题型六
等边三角形的性质与判定
(2) ∵△ADC≌△BEC
∴∠ACP=∠BCQ,AC=BC,∠CAP=∠CBQ
∴△APC≌△BQC(ASA)
方 程
例题2 如图,C为线段AE 上一动点,(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.
求证:(3) △PCQ是等边三角形
题型六
等边三角形的性质与判定
(3) ∵CD=CE,∠DCP=∠ECQ=60°,∠ADC=∠BEC
∴△CDP≌△CEQ(ASA).
∴CP=CQ,
∴∠CPQ=∠CQP=60°
∴△CPQ是等边三角形
方 程
例题1 (1) 问题发现
如图1,△ACB和△DCE 均为等边三角形,点A、D、E在同一直线上,连接BE,求∠AEB的度数
题型七
手拉手模型
解:(1) ∵△ACB 和△DCE 均为等边三角形
∴CA=CB,CD=CE,∠ACB=∠DCE=60°
∴∠ACD=60°-∠CDB=∠BCE.
在△ACD和△BCE 中
∴△ACD≌△BCE (SAS)
∴∠ADC=∠BEC
∵△DCE 为等边三角形
∴∠CDE=∠CED=60°
∵点A,D,E在同一直线上,
∴∠ADC=120°
∴∠BEC=120°
∴∠AEB=∠BEC-∠CED=60°
方 程
例题1 (2)拓展探究
如图2,△ACB和△DCE 均为等腰直角三角形,∠ACB=∠DCE=90°点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请求∠AEB 的度数及线段 CM、AE、BE之间的数量关系,并说明理由.
题型七
手拉手模型
∴△ACD≌△BCE (SAS)
∴AD=BE,∠ADC=∠BEC
∵△DCE 为等腰直角三角形,
∴∠CDE=∠CED=45°
∵点A,D,E在同一直线上
∴∠ADC=135°
∴∠BEC=135°
∴∠AEB=∠BEC- ∠CED=90°
∵CD=CE,CM⊥DE,
∴DM=ME.
(2) ∠AEB=90°,AE=BE+2CM
理由:∵△ACB 和△DCE 均为等腰直角三角形
∴CA=CB,CD=CE,∠ACB=∠DCE=90°
∴∠ACD=∠BCE
∵∠DCE=90°,
∴DM=ME=CM
∴AE=AD+DE=BE+2CM
在△ACD和△BCE中,
方 程
例题1 如图,∠AOB=30°,点M、N分别是射线 OB、OA上的动点,点P为∠AOB内一点,且OP=4,则△PMN的周长的最小值为 ( )
题型八
轴对称最短路径问题
A.2 B.4 C.6 D.8
解: 分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M'、N',连接OC、OD、PM'、PN’
∵点P关于 OA 的对称点为 C,
∴PM'=CM',OP=OC,∠COB=∠POB
∵点P关于 OB的对称点为 D
∴PN'=DN',OP=OD,∠DOA= ∠POA,
∴OC=OD=OP=4,∠COD=∠COB+∠POB+∠POA+∠DOA
=2∠POA+2∠POB=2∠AOB=60°.
∴△COD 是等边三角形,
∴CD=OC=OD=4.
∴当M、N分别与M'、N'重合时,
△PMN的周长的最小值=PM'+M'N'+PN'=DN'+M'N'+CM'=CD=4
故选:B.
方 程
例题2 如图,在四边形ABCD中,∠A=∠C=90°,∠B=34°,在边AB、BC分别找一点E、F使△DEF的周长最小,此时∠EDF=_________.
题型八
轴对称最短路径问题
解: 如图,作点D关于BA的对称点P,点D关于BC的对称点Q,连接PQ,交AB于E',交BC于 F',则点 E',F'即为所求.
∵四边形ABCD中,∠A=∠C=90°,∠B=α
∴∠ADC=180°- α,
由轴对称知,△ADE'=△P,△CDF'=∠Q
在△PDQ中,△P+Q=180°- △ADC
=180°- (180° - 34°)
=34°
∴∠ADE'+∠CDF'=∠P+∠Q=34°,
∴∠E'DF'=∠ADC- (∠ADE'+∠CDF')
=180°- 68°
=112°
故答案为: 112°
