华东师大版九年级数学上册21.2 .3 二次根式的除法 课件(19张ppt)
文档属性
| 名称 | 华东师大版九年级数学上册21.2 .3 二次根式的除法 课件(19张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 25.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 14:51:29 | ||
图片预览






文档简介
(共19张PPT)
九年级数学上(HS)
第2课时 二次根式的除法
21.2 二次根式的乘除
*
*
*
*
学习目标
课程导入
单击此处输入你的正文,文字是您思想的提炼,为了最终演示发布的良好效果,请尽量言简意赅的阐述观点;根据需要可酌情增减文字,以便观者可以准确理解您所传达的信息。单击此处输入你的正文,文字是您思想的提炼,为了最终演示发布的良好效果,请尽量言简意赅的阐述观点;根据需要可酌情增减文字,以便观者可以准确理解您所传达的信息。
1.掌握二次根式的除法法则及商的算术平方根的性质;(重点)
2.会利用除法法则进行二次根式的运算.(难点)
*
*
温故而知新
关键:将被开方数因式分解或因数分解,使被开方数出现“完全平方数”或“偶次方因式”.
二次根式的两个基本性质:
|a|,
二次根式的乘法:
(a≥0,b≥0)
(a≥0,b≥0)
如何化简二次根式
*
*
本课内容
单击此处输入你的正文,文字是您思想的提炼,为了最终演示发布的良好效果,请尽量言简意赅的阐述观点;根据需要可酌情增减文字,以便观者可以准确理解您所传达的信息。单击此处输入你的正文,文字是您思想的提炼,为了最终演示发布的良好效果,请尽量言简意赅的阐述观点;根据需要可酌情增减文字,以便观者可以准确理解您所传达的信息。
(2)
(3)
_______;
_______;
_______;
_______;
_______;
_____ __.
计算下列各式,观察计算结果,你能发现什么规律?
二次根式的除法法则及运算
我们知道,两个二次根式可以进行乘法运算,那么,两个二次根式能否进行除法运算呢?
知识精讲
*
*
单击此处输入你的正文,文字是您思想的提炼,为了最终演示发布的良好效果,请尽量言简意赅的阐述观点;根据需要可酌情增减文字
单击此处输入你的正文,文字是您思想的提炼,为了最终演示发布的良好效果,请尽量言简意赅的阐述观点;根据需要可酌情增减文字
一般地,二次根式的除法法则
(a≥0,b>0)
两个二次根式相除,等于把被开方数相除,作为商的被开方数.
思考:等式中的a和b有没有条件的限制?
含有系数的二次根式相除:可类比单项式除以单项式法则
(a≥0,b>0,n≠0)
知识精讲
*
*
典例精析
解:
典例精析
例1 计算:
最后结果不能含有开得尽方的因数或因式,同时分母不能含二次根式
*
*
典例精析
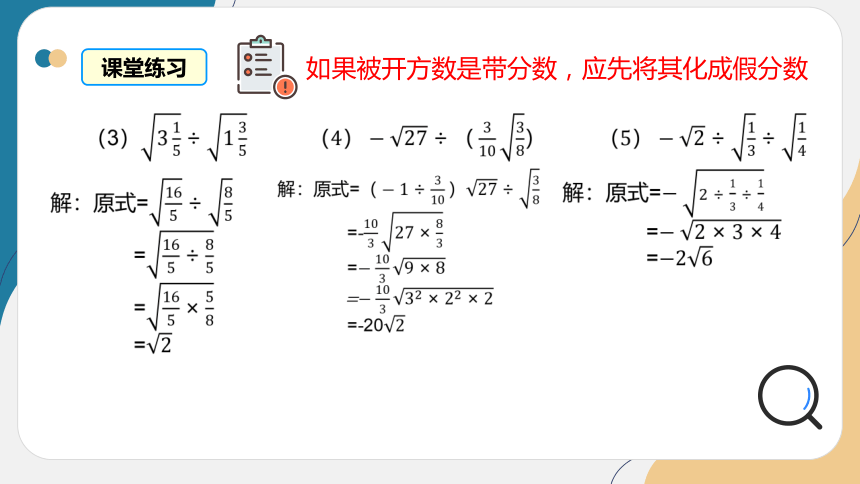
课堂练习
(3)
解:原式=
=
=
=
如果被开方数是带分数,应先将其化成假分数
解:原式=
=-
=
=
=-20
解:原式=
=
=
*
*
典例精析
公式的逆用
商的算术平方根的性质及化简
商的算术平方根
知识精讲
*
*
典例精析
(3)(x≥0,y>0) (4)
解:(1)原式=
(2)原式===
(3) 原式==
(4)原式===
典例精析
*
*
最简二次根式的概念及判断
观察上面各数并思考:
(1)你觉得这些数能否再化简,它们已经是最简二次根式了吗?
(2)这些结果有什么共同特点,你认为一个二次根式满足什么条件就可以说它是最简二次根式了?
知识精讲
*
*
可以发现这些式子有如下两个特点:
(1)被开方数不含分母(分母中不能被开方数);
(2)被开方数中不含能开得尽方的因数或因式.
我们把满足上述两个条件的二次根式,叫做最简二次根式.
简记为:分母无根号,根号无分母
知识精讲
*
*
√√
典例精析
下列各项式子中,哪些是最简二次根式
√
√
√
*
*
知识精讲
(1) (2)
被开方数中含能开得尽方的因数
解:原式=
=
=4
解:原式=
=
=(a+3)
如果被开方数是整数或整式,先将它分解因数或分解因式,再利用积的算术平方根的性质,把开得尽方的因数或因式开出来,从而将式子化简
*
*
课堂练习
(2)
解:原式=
4
解:原式=
=
=2xy(x+y)
整式分解的时候注意字母条件
*
*
(1)
知识精讲
被开方数中含有分母,分母中含有根号
解:原式=
=
解:原式=
=
分母从无理数变为有理数这种方法称之为分母有理化,即把分母中的根号化去的过程.
如果被开方数是分式或分数(包括小数),先利用上的算术平方跟的性质把它写成分式的形式,如果分母开得尽方,就把它开出来;如果分母开不尽方,就利用分母有理化的方法来化简
=
=
*
*
课堂练习
(1) (2)
*
*
知识精讲
(1)
解:原式=
=
分母有理化口诀:
分母有理化,
分式性质来当家。
找出有理化因式,
(2)
解:原式=
=
(a+b)(a-b)=
*
*
1. 利用商的算术平方根的性质化简二次根式.
2. 二次根式的除法有两种常用方法:
(1)利用公式: ((a≥0,b>0))
(2)把除法先写成分式的形式,再进行分母有理化运算.
3.最简二次根式的概念
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
4.分母有理化:把分母中的根号化去的过程.
课堂小结
谢谢大家观看
*
*
九年级数学上(HS)
第2课时 二次根式的除法
21.2 二次根式的乘除
*
*
*
*
学习目标
课程导入
单击此处输入你的正文,文字是您思想的提炼,为了最终演示发布的良好效果,请尽量言简意赅的阐述观点;根据需要可酌情增减文字,以便观者可以准确理解您所传达的信息。单击此处输入你的正文,文字是您思想的提炼,为了最终演示发布的良好效果,请尽量言简意赅的阐述观点;根据需要可酌情增减文字,以便观者可以准确理解您所传达的信息。
1.掌握二次根式的除法法则及商的算术平方根的性质;(重点)
2.会利用除法法则进行二次根式的运算.(难点)
*
*
温故而知新
关键:将被开方数因式分解或因数分解,使被开方数出现“完全平方数”或“偶次方因式”.
二次根式的两个基本性质:
|a|,
二次根式的乘法:
(a≥0,b≥0)
(a≥0,b≥0)
如何化简二次根式
*
*
本课内容
单击此处输入你的正文,文字是您思想的提炼,为了最终演示发布的良好效果,请尽量言简意赅的阐述观点;根据需要可酌情增减文字,以便观者可以准确理解您所传达的信息。单击此处输入你的正文,文字是您思想的提炼,为了最终演示发布的良好效果,请尽量言简意赅的阐述观点;根据需要可酌情增减文字,以便观者可以准确理解您所传达的信息。
(2)
(3)
_______;
_______;
_______;
_______;
_______;
_____ __.
计算下列各式,观察计算结果,你能发现什么规律?
二次根式的除法法则及运算
我们知道,两个二次根式可以进行乘法运算,那么,两个二次根式能否进行除法运算呢?
知识精讲
*
*
单击此处输入你的正文,文字是您思想的提炼,为了最终演示发布的良好效果,请尽量言简意赅的阐述观点;根据需要可酌情增减文字
单击此处输入你的正文,文字是您思想的提炼,为了最终演示发布的良好效果,请尽量言简意赅的阐述观点;根据需要可酌情增减文字
一般地,二次根式的除法法则
(a≥0,b>0)
两个二次根式相除,等于把被开方数相除,作为商的被开方数.
思考:等式中的a和b有没有条件的限制?
含有系数的二次根式相除:可类比单项式除以单项式法则
(a≥0,b>0,n≠0)
知识精讲
*
*
典例精析
解:
典例精析
例1 计算:
最后结果不能含有开得尽方的因数或因式,同时分母不能含二次根式
*
*
典例精析
课堂练习
(3)
解:原式=
=
=
=
如果被开方数是带分数,应先将其化成假分数
解:原式=
=-
=
=
=-20
解:原式=
=
=
*
*
典例精析
公式的逆用
商的算术平方根的性质及化简
商的算术平方根
知识精讲
*
*
典例精析
(3)(x≥0,y>0) (4)
解:(1)原式=
(2)原式===
(3) 原式==
(4)原式===
典例精析
*
*
最简二次根式的概念及判断
观察上面各数并思考:
(1)你觉得这些数能否再化简,它们已经是最简二次根式了吗?
(2)这些结果有什么共同特点,你认为一个二次根式满足什么条件就可以说它是最简二次根式了?
知识精讲
*
*
可以发现这些式子有如下两个特点:
(1)被开方数不含分母(分母中不能被开方数);
(2)被开方数中不含能开得尽方的因数或因式.
我们把满足上述两个条件的二次根式,叫做最简二次根式.
简记为:分母无根号,根号无分母
知识精讲
*
*
√√
典例精析
下列各项式子中,哪些是最简二次根式
√
√
√
*
*
知识精讲
(1) (2)
被开方数中含能开得尽方的因数
解:原式=
=
=4
解:原式=
=
=(a+3)
如果被开方数是整数或整式,先将它分解因数或分解因式,再利用积的算术平方根的性质,把开得尽方的因数或因式开出来,从而将式子化简
*
*
课堂练习
(2)
解:原式=
4
解:原式=
=
=2xy(x+y)
整式分解的时候注意字母条件
*
*
(1)
知识精讲
被开方数中含有分母,分母中含有根号
解:原式=
=
解:原式=
=
分母从无理数变为有理数这种方法称之为分母有理化,即把分母中的根号化去的过程.
如果被开方数是分式或分数(包括小数),先利用上的算术平方跟的性质把它写成分式的形式,如果分母开得尽方,就把它开出来;如果分母开不尽方,就利用分母有理化的方法来化简
=
=
*
*
课堂练习
(1) (2)
*
*
知识精讲
(1)
解:原式=
=
分母有理化口诀:
分母有理化,
分式性质来当家。
找出有理化因式,
(2)
解:原式=
=
(a+b)(a-b)=
*
*
1. 利用商的算术平方根的性质化简二次根式.
2. 二次根式的除法有两种常用方法:
(1)利用公式: ((a≥0,b>0))
(2)把除法先写成分式的形式,再进行分母有理化运算.
3.最简二次根式的概念
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
4.分母有理化:把分母中的根号化去的过程.
课堂小结
谢谢大家观看
*
*
