北师大版四年级下册数学 第二单元 探索三角形三边关系(教学设计)
文档属性
| 名称 | 北师大版四年级下册数学 第二单元 探索三角形三边关系(教学设计) |

|
|
| 格式 | docx | ||
| 文件大小 | 66.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 00:00:00 | ||
图片预览



文档简介
探索三角形三边关系教学设计
【教学内容】
北师大版小学数学四年级下册《探索三角形三边的关系》
研究背景: 北师大版四年级下册第二单元“三角形边的认识”中的三角形的三边关系。该课时是在学生初步了解三角形的定义,三角形的稳定性的基础上,进一步探索三角形的又一特征:即三角形的任意两边的和大于第三边。加深学生对三角形的认识,同时为今后学生学习三角形和四边形的联系和区别,甚至为中学学习勾股定理等知识打下基础。这个知识点原来在初中进行学习,但新课改后下放到小学四年级。10岁的孩子能接受吗?“任意”这个词对很多数学生来说是比较抽象、难以理解的,通过怎样的教学才能让学生对三角形三边之间的大小关系有更深的理解?这是我课前挺担心的问题。通过查阅资料及充分考虑学生身心的发展特征,我设计了如下基本思路:学生对图形性质的体验是建立在数学实践活动中进行的,我的课堂将为孩子们提供大量观察、操作、思考、想象、交流等活动,使学生在有挑战性的、充满想象和富含思考的过程中,体验三角形的任意两边的和大于第三边这个性质,并同时积累数学活动经验,发展空间观念。
【学情分析】
《三角形三边的关系》是北师大版四年级下册的一个内容。教材内容分为三部分:先是用四组小棒动手围一围。然后是把实验结果记录下来,并且进行计算,最后通过数据的比较去发现三边关系。这部分内容是建立在学生已经对三角形有了初步认识的基础上,进一步研究三角形的新特性——即三边关系。其实对于平面图形边的关系的探索学生也不陌生,在之前学生已经有了去发现长方形、正方形等图形的边的特点。只不过这些图形中边的关系更多的是等量关系,或者两个量的大小关系。而这节课却是要去发现三边关系,所以对学生来说既有知识迁移的基础,同时是非常有挑战性的。
另外,新课标指出小学阶段几何证明教学的目的不应当是追求证明的技巧,而重在养成“说明有据”的态度。所以编者十分注意变证明结论为探索性实验和发现,这也是为什么编者要把这一内容放在“探索与发现”这个主题单元中的原因,就是想让学生参与比较严谨的数学研究过程中,从而体验逻辑证明的意义。
【教学目标】
1. 知识技能目标: 使学生知道“三角形中任意两边的和大于第三边”,能运用这一关系解决简单的实际问题。
2.过程与方法目标: 经历三角形三边关系的探索过程,在这一过程中提高学生观察、分析、概括等能力,初步感知归纳推理,感知由反及正的数学思想。
3.情感与态度目标:让学生在探索过程中体验数学学习的乐趣,并培养其团结协助的精神。
【教学重难点】
教学重点:三角形三边关系的探究过程。
教学难点:从具体到抽象去发现规律,获得结论。
【教、学具准备】
多媒体课件、小棒若干、活动记录单
【教学过程】
一、引发矛盾,提出研究问题
1.复习三角形的定义,再现三角形的表象。
(1)说说下面的图形哪些是三角形。
(2)为什么后面两个图形不是三角形呢?让学生明白在围三角形时一定要做到首尾相接。
2.给你三根小棒,你能围成一个三角形吗?
抽生上来动手实践,让学生从无意到有惑,发现任意给三根小棒不一定能围成三角形。
猜测:能否围成三角形和什么有关,有怎样的关系呢?
提示课题:探索三角形三边关系。
二、实践操作,积累研究材料。
1.学生分组活动前提出了探究的内容和要求:
(1)任取三根小棒,看看能不能围成三角形。
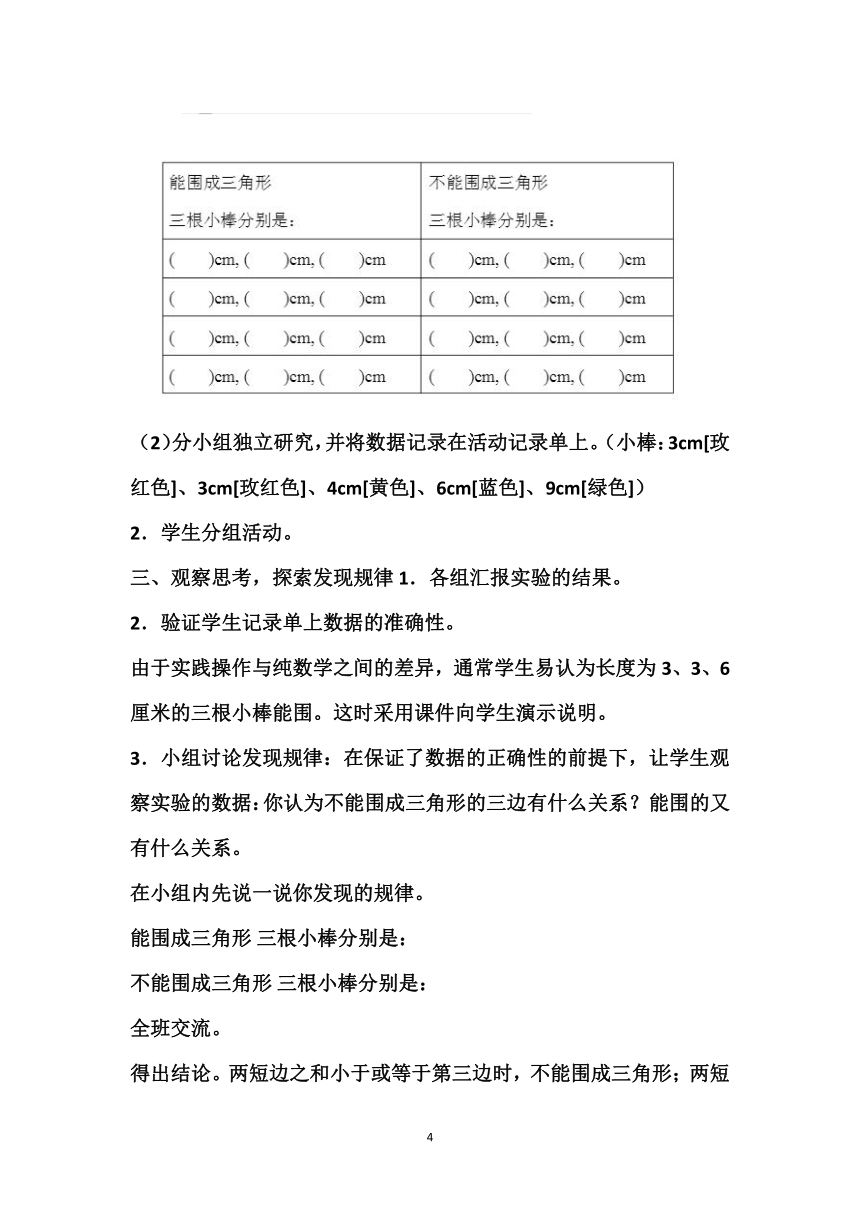
(2)分小组独立研究,并将数据记录在活动记录单上。 (小棒:3cm[玫红色]、3cm[玫红色]、4cm[黄色]、6cm[蓝色]、9cm[绿色])
2.学生分组活动。
三、观察思考,探索发现规律 1.各组汇报实验的结果。
2.验证学生记录单上数据的准确性。
由于实践操作与纯数学之间的差异,通常学生易认为长度为3、3、6厘米的三根小棒能围。这时采用课件向学生演示说明。
3.小组讨论发现规律:在保证了数据的正确性的前提下,让学生观察实验的数据:你认为不能围成三角形的三边有什么关系?能围的又有什么关系。
在小组内先说一说你发现的规律。
能围成三角形 三根小棒分别是:
不能围成三角形 三根小棒分别是:
全班交流。
得出结论。两短边之和小于或等于第三边时,不能围成三角形;两短边之和大于第三边时,能围成三角形。
演绎:
刚才发现的规律是不是适合于任何情况呢?通过电脑进行演绎说明,这个结论普遍性。
深化:
学生发现三角形里,两短边之和大于第三边。 字母表示规律:
如果用字母a表示短边,b表示另一条较短的边,c表示长边。你能用字母把刚才发现的规律表示出来吗?
学生进行理性的逻辑分析。如果a+b>c,那么a+c的和与b相比呢?b+c的和与a相比呢?
概括抽象出三角形的三边关系:任意两边之和大于第三边。 加深对“任意”一词的理解。你能说说“任意”是什么意思吗 四、巩固深化,创新运用规律 1.巩固性训练
利用三角形三边关系,判断下面哪组小棒能围成三角形。
8cm、5cm 、6cm(能围)
5cm、7cm 、2cm(不能围)
3cm、4cm 、5cm(能围)
4cm、4cm 、4cm(能围)
让学生思考:我们在判断能否围三角形时,有没有什么简捷的方法呢?
2.拓展性训练。
说一说在课前围三角形的活动中,为什么7厘米、10厘米、8厘米一组的小棒能围成三角形?为什么7厘米、10厘米、18厘米一组的小棒不能围成三角形?
3.课外延伸训练
请你给7厘米、10厘米的二根小棒,再配上一根小棒,使它们能围成一个三角形。说说你有多少种不同的配法?
教后反思:
在信息如此畅通的今天,为我总想站在“巨人”的肩膀上提升自己的课堂教学提供了可能。在课前,我也参考了包括华应龙、丁杭缨等名师在内的无数个教案。但最终没有生搬硬套,摆脱了思想上的禁锢,上出了符合我自己“班情、学情 ”的一节好课。 总结成功的经验,本节课有三大亮点:
1. 教学设计基于学生的实际
本节课与一般的教学设计从步骤看最大的不同是:先研究“三角形边的关系”得出“较短两边之和大于第三边”,经过讨论验证后用“任意”代替“较短”,条理非常清晰。我个人觉得:对于学生来说,围绕“任意的三根小棒能否围成一个三角形?”这个问题自己操作,发现有的能围成,有的围不成。并进一步在操作之中探究什么情况下不能围成三角形,为什么?初步直观感知到的三条边之间的关系确实是“较短两边之和大于第三边”,而不是书中所述的“三角形任意两边的和大于第三边”。 用学生自己的话说;在判断三条线段能否组成三角形时,用“较短两边之和大于第三边”,确实十分的方便快捷。因为较短的两条边之和如果大于第三条边,则说明任意一条较短的边与最长的一边之和肯定大于第三条边,这也就更进一步说明这个三角形的任意两边之和大于第三边。这也为“任意”这个词做了最好的解释。
2.材料选择便于学生操作 选用针线和吸管进行操作,串连方便,用手一掐就知道能不能围成三角形,这样不仅便于操作,还便于交流反馈时一目了然,不会造成没必要的争议:能拼成三角形、不能拼成三角形、两条线段成直线并与第三条线重合。你想剪怎样的三段,数据材料来自学生自己提供的,也使材料的可信性增强。整个活动简单,既能培养学生的空间想像能力,又培养了学生的动手能力,同时对三角形三边关系有了比较形象的认识。教学效果好。学生能操作又会操作,数学性和探索性都很强。
3.练习设计发展空间观念
练习设计,从易到难重新编排,适度拓展,一题多用,如练习1从能否围成三角形出发,穿插了直角三角形、等边三角形、等腰三角形、勾股定理、图形与代数、区间等等一系列代数与几何的数学知识。追问三根小棒如能围成三角形会是一个怎样的三角形,让学生先想象,再课件演示,这有助学生空间观念的形成。
有人说,良好的教育一定要致力于学生用自己的眼睛去观察,用自己的心灵去感悟,用自己的头脑去判别,用自己的语言去表达,才能使一个人成为真正的人,成为他自己。本节课,我始终抓住这一教育思想对学生施教,让学生在学习中感受到了自己的存在与价值,体验到了主动建构知识的快乐。同时培养了学生创造的欲望,创造的能力。
【教学内容】
北师大版小学数学四年级下册《探索三角形三边的关系》
研究背景: 北师大版四年级下册第二单元“三角形边的认识”中的三角形的三边关系。该课时是在学生初步了解三角形的定义,三角形的稳定性的基础上,进一步探索三角形的又一特征:即三角形的任意两边的和大于第三边。加深学生对三角形的认识,同时为今后学生学习三角形和四边形的联系和区别,甚至为中学学习勾股定理等知识打下基础。这个知识点原来在初中进行学习,但新课改后下放到小学四年级。10岁的孩子能接受吗?“任意”这个词对很多数学生来说是比较抽象、难以理解的,通过怎样的教学才能让学生对三角形三边之间的大小关系有更深的理解?这是我课前挺担心的问题。通过查阅资料及充分考虑学生身心的发展特征,我设计了如下基本思路:学生对图形性质的体验是建立在数学实践活动中进行的,我的课堂将为孩子们提供大量观察、操作、思考、想象、交流等活动,使学生在有挑战性的、充满想象和富含思考的过程中,体验三角形的任意两边的和大于第三边这个性质,并同时积累数学活动经验,发展空间观念。
【学情分析】
《三角形三边的关系》是北师大版四年级下册的一个内容。教材内容分为三部分:先是用四组小棒动手围一围。然后是把实验结果记录下来,并且进行计算,最后通过数据的比较去发现三边关系。这部分内容是建立在学生已经对三角形有了初步认识的基础上,进一步研究三角形的新特性——即三边关系。其实对于平面图形边的关系的探索学生也不陌生,在之前学生已经有了去发现长方形、正方形等图形的边的特点。只不过这些图形中边的关系更多的是等量关系,或者两个量的大小关系。而这节课却是要去发现三边关系,所以对学生来说既有知识迁移的基础,同时是非常有挑战性的。
另外,新课标指出小学阶段几何证明教学的目的不应当是追求证明的技巧,而重在养成“说明有据”的态度。所以编者十分注意变证明结论为探索性实验和发现,这也是为什么编者要把这一内容放在“探索与发现”这个主题单元中的原因,就是想让学生参与比较严谨的数学研究过程中,从而体验逻辑证明的意义。
【教学目标】
1. 知识技能目标: 使学生知道“三角形中任意两边的和大于第三边”,能运用这一关系解决简单的实际问题。
2.过程与方法目标: 经历三角形三边关系的探索过程,在这一过程中提高学生观察、分析、概括等能力,初步感知归纳推理,感知由反及正的数学思想。
3.情感与态度目标:让学生在探索过程中体验数学学习的乐趣,并培养其团结协助的精神。
【教学重难点】
教学重点:三角形三边关系的探究过程。
教学难点:从具体到抽象去发现规律,获得结论。
【教、学具准备】
多媒体课件、小棒若干、活动记录单
【教学过程】
一、引发矛盾,提出研究问题
1.复习三角形的定义,再现三角形的表象。
(1)说说下面的图形哪些是三角形。
(2)为什么后面两个图形不是三角形呢?让学生明白在围三角形时一定要做到首尾相接。
2.给你三根小棒,你能围成一个三角形吗?
抽生上来动手实践,让学生从无意到有惑,发现任意给三根小棒不一定能围成三角形。
猜测:能否围成三角形和什么有关,有怎样的关系呢?
提示课题:探索三角形三边关系。
二、实践操作,积累研究材料。
1.学生分组活动前提出了探究的内容和要求:
(1)任取三根小棒,看看能不能围成三角形。
(2)分小组独立研究,并将数据记录在活动记录单上。 (小棒:3cm[玫红色]、3cm[玫红色]、4cm[黄色]、6cm[蓝色]、9cm[绿色])
2.学生分组活动。
三、观察思考,探索发现规律 1.各组汇报实验的结果。
2.验证学生记录单上数据的准确性。
由于实践操作与纯数学之间的差异,通常学生易认为长度为3、3、6厘米的三根小棒能围。这时采用课件向学生演示说明。
3.小组讨论发现规律:在保证了数据的正确性的前提下,让学生观察实验的数据:你认为不能围成三角形的三边有什么关系?能围的又有什么关系。
在小组内先说一说你发现的规律。
能围成三角形 三根小棒分别是:
不能围成三角形 三根小棒分别是:
全班交流。
得出结论。两短边之和小于或等于第三边时,不能围成三角形;两短边之和大于第三边时,能围成三角形。
演绎:
刚才发现的规律是不是适合于任何情况呢?通过电脑进行演绎说明,这个结论普遍性。
深化:
学生发现三角形里,两短边之和大于第三边。 字母表示规律:
如果用字母a表示短边,b表示另一条较短的边,c表示长边。你能用字母把刚才发现的规律表示出来吗?
学生进行理性的逻辑分析。如果a+b>c,那么a+c的和与b相比呢?b+c的和与a相比呢?
概括抽象出三角形的三边关系:任意两边之和大于第三边。 加深对“任意”一词的理解。你能说说“任意”是什么意思吗 四、巩固深化,创新运用规律 1.巩固性训练
利用三角形三边关系,判断下面哪组小棒能围成三角形。
8cm、5cm 、6cm(能围)
5cm、7cm 、2cm(不能围)
3cm、4cm 、5cm(能围)
4cm、4cm 、4cm(能围)
让学生思考:我们在判断能否围三角形时,有没有什么简捷的方法呢?
2.拓展性训练。
说一说在课前围三角形的活动中,为什么7厘米、10厘米、8厘米一组的小棒能围成三角形?为什么7厘米、10厘米、18厘米一组的小棒不能围成三角形?
3.课外延伸训练
请你给7厘米、10厘米的二根小棒,再配上一根小棒,使它们能围成一个三角形。说说你有多少种不同的配法?
教后反思:
在信息如此畅通的今天,为我总想站在“巨人”的肩膀上提升自己的课堂教学提供了可能。在课前,我也参考了包括华应龙、丁杭缨等名师在内的无数个教案。但最终没有生搬硬套,摆脱了思想上的禁锢,上出了符合我自己“班情、学情 ”的一节好课。 总结成功的经验,本节课有三大亮点:
1. 教学设计基于学生的实际
本节课与一般的教学设计从步骤看最大的不同是:先研究“三角形边的关系”得出“较短两边之和大于第三边”,经过讨论验证后用“任意”代替“较短”,条理非常清晰。我个人觉得:对于学生来说,围绕“任意的三根小棒能否围成一个三角形?”这个问题自己操作,发现有的能围成,有的围不成。并进一步在操作之中探究什么情况下不能围成三角形,为什么?初步直观感知到的三条边之间的关系确实是“较短两边之和大于第三边”,而不是书中所述的“三角形任意两边的和大于第三边”。 用学生自己的话说;在判断三条线段能否组成三角形时,用“较短两边之和大于第三边”,确实十分的方便快捷。因为较短的两条边之和如果大于第三条边,则说明任意一条较短的边与最长的一边之和肯定大于第三条边,这也就更进一步说明这个三角形的任意两边之和大于第三边。这也为“任意”这个词做了最好的解释。
2.材料选择便于学生操作 选用针线和吸管进行操作,串连方便,用手一掐就知道能不能围成三角形,这样不仅便于操作,还便于交流反馈时一目了然,不会造成没必要的争议:能拼成三角形、不能拼成三角形、两条线段成直线并与第三条线重合。你想剪怎样的三段,数据材料来自学生自己提供的,也使材料的可信性增强。整个活动简单,既能培养学生的空间想像能力,又培养了学生的动手能力,同时对三角形三边关系有了比较形象的认识。教学效果好。学生能操作又会操作,数学性和探索性都很强。
3.练习设计发展空间观念
练习设计,从易到难重新编排,适度拓展,一题多用,如练习1从能否围成三角形出发,穿插了直角三角形、等边三角形、等腰三角形、勾股定理、图形与代数、区间等等一系列代数与几何的数学知识。追问三根小棒如能围成三角形会是一个怎样的三角形,让学生先想象,再课件演示,这有助学生空间观念的形成。
有人说,良好的教育一定要致力于学生用自己的眼睛去观察,用自己的心灵去感悟,用自己的头脑去判别,用自己的语言去表达,才能使一个人成为真正的人,成为他自己。本节课,我始终抓住这一教育思想对学生施教,让学生在学习中感受到了自己的存在与价值,体验到了主动建构知识的快乐。同时培养了学生创造的欲望,创造的能力。
