2023-2024学年人教版数学七年级上册 4.3 角 同步练习 (含答案)
文档属性
| 名称 | 2023-2024学年人教版数学七年级上册 4.3 角 同步练习 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 122.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 18:27:20 | ||
图片预览


文档简介
4.3 角
一、单选题
1.把8.32°用度、分、秒表示正确的是( )
A.8°3′2″ B.8°30′2″
C.8°19′12″ D.8°19 ′20″
2.如图,小于平角的角共有( )
A.10个 B.9个 C.8个 D.4个
3.一个角是这个角的余角的2倍,则这个角的度数是( )
A.30° B.45° C.60° D.75°
4.如图, ,以 为一边作 ,则 的度数为( )
A. B.
C. 或 D. 或
5.如图,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD=150°,则∠BOC等于( )
A.30° B.45° C.50° D.60°
6.如图,小明在操场上从A点出发,先沿南偏东30°方向走到B点,再沿南偏东60°方向走到C点.这时,∠ABC的度数是( )
A.120° B.135° C.150° D.160°
7.如图,∠AOB=90°,OC平分∠AOB,OE平分∠AOD,若∠AOD=y°,则∠EOC的度数为( )
A. B. C. D.
8.如图,已知∠1=∠2,∠3=∠4,∠BOD= ∠AOB=90°.下列判断:①射线OF是∠BOE的角平分线;②∠DOE的补角是∠BOC;③∠AOC的余角只有∠COD;④∠DOE的余角有∠BOE和∠COD;⑤∠COD=∠BOE.其中正确的有( )
A.5个 B.4个 C.3个 D.2个
二、填空题
9.若一个角的补角是 ,则这个角的余角是 .
10.如图所示,两块三角板的直角顶点O重叠在一起,且OB恰好平分∠COD,则∠AOD的度数是 度.
11.如图,时钟显示时间为4:00,此时,时针与分针所成夹角为 度.
12.如图,点A,O,C在一条直线上,∠AOD=120°,且∠AOB:∠COD=3:5,则∠COD的度数为 ,∠BOC的度数为
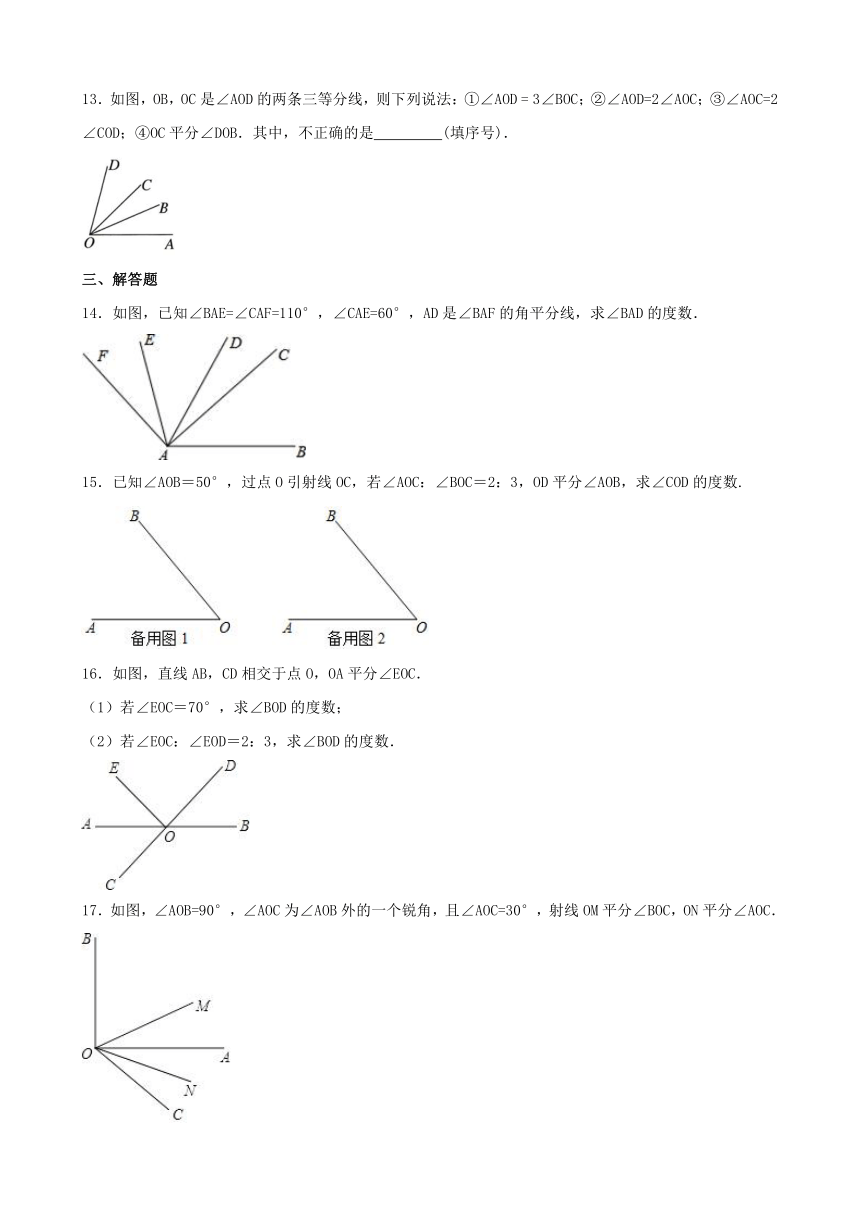
13.如图,OB,OC是∠AOD的两条三等分线,则下列说法:①∠AOD = 3∠BOC;②∠AOD=2∠AOC;③∠AOC=2∠COD;④OC平分∠DOB.其中,不正确的是 (填序号).
三、解答题
14.如图,已知∠BAE=∠CAF=110°,∠CAE=60°,AD是∠BAF的角平分线,求∠BAD的度数.
15.已知∠AOB=50°,过点O引射线OC,若∠AOC:∠BOC=2:3,OD平分∠AOB,求∠COD的度数.
16.如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
17.如图,∠AOB=90°,∠AOC为∠AOB外的一个锐角,且∠AOC=30°,射线OM平分∠BOC,ON平分∠AOC.
(1)求∠MON的度数;
(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中∠AOC=β(β为锐角),其他条件不变,求∠MON的度数.
18.点C,D是半圆弧上的两个动点,在运动的过程中保持∠COD=80°.
(1)如图1,OM平分∠AOC,ON平分∠BOD,求∠MON的度数;
(2)如图2,若∠AOC=x°,OM平分∠AOD,ON平分∠BOC,求∠MON的度数.
参考答案
1.C
2.B
3.C
4.D
5.A
6.C
7.C
8.B
9.
10.135
11.120
12.60°;144°
13.②
14.解:由∠BAE=110°,∠CAE=60°,可得∠BAC=110°﹣60°=50°,结合∠CAF=110°,可得∠BAF=110°+50°=160°,再由AD平分∠BAF即可得∠BAD=80°.
试题解析:
∵∠BAE=110°,∠CAE=60°,
∴∠BAC=110°﹣60°=50°,
又∵∠CAF=110°,
∴∠BAF=110°+50°=160°,
又∵AD是∠BAF的角平分线,
∴∠BAD= ∠BAF= ×160°=80°.
15.解:分两种情况讨论:
( 1 )射线OC在∠AOB的内部,如图①;
设∠AOC=2x,则∠COB=3x,则2x+3x=50°,∴x=10°,∠AOC=2x=20°,∠AOD 50°=25°,∴∠COD=∠AOD﹣∠AOC=25°﹣20°=5°;
( 2 )射线OC在∠AOB的外部,如图②.
设∠AOC=2x,则∠COB=3x,则∠AOB=3x﹣2x=x=50°,∴∠AOC=2x=100°
∠AOD=25°,∴∠COD=∠AOC+∠AOD=100°+25°=125°.
综上所述:∠COD=5°或∠COD=125°.
16.(1)解:∵OA平分∠EOC,
∴∠AOC= ∠EOC= ×70°=35°,
∴∠BOD=∠AOC=35°
(2)解:设∠EOC=2x,∠EOD=3x,根据题意得2x+3x=180°,解得x=36°,
∴∠EOC=2x=72°,
∴∠AOC= ∠EOC= ×72°=36°,
∴∠BOD=∠AOC=36°
17.(1)解:∵∠AOB=90°,∠AOC=30°,
∴∠BOC=120°.
∵OM平分∠BOC,ON平分∠AOC,
∴∠COM=60°,∠CON=15°,
∴∠MON=∠COM﹣∠CON=45°
(2)解:∵∠AOB=α,∠AOC=30°,
∴∠BOC=α+30°.
∵OM平分∠BOC,ON平分∠AOC,
∴∠COM= α+15°,∠CON=15°,
∴∠MON=∠COM﹣∠CON= α
(3)解:∵∠AOB=90°,∠AOC=β,
∴∠BOC=90°+β.
∵OM平分∠BOC,ON平分∠AOC,
∴∠COM=45°+ β,∠CON= β,
∴∠MON=∠COM﹣∠CON=45°
18.(1)解;如图1,
∵OM平分∠AOC,ON平分∠BOD,
∴∠MOC= ∠AOC,∠NOD= ∠BOD,
又∵∠COD=80°,
∴∠AOC+∠BOD=100°﹣80°=100°,
∴∠MON=∠COD+∠MOC+∠NOD=80°+ ×100°=130°;
(2)解:如图2,∠AOC=x°,则∠AOD=x°+80°,∠BOD=100°﹣x°,
∵OM平分∠AOD
∴∠AOM= ∠AOD= x°+40°;
又∵ON平分∠BOC
∴∠BON= ∠BOC= (180°﹣x°)=90°﹣ x°,
∴∠MON=180°﹣(∠AOM+∠BON)=180°﹣( x°+40°+90°﹣ x°)
=180°﹣130°
=50°
一、单选题
1.把8.32°用度、分、秒表示正确的是( )
A.8°3′2″ B.8°30′2″
C.8°19′12″ D.8°19 ′20″
2.如图,小于平角的角共有( )
A.10个 B.9个 C.8个 D.4个
3.一个角是这个角的余角的2倍,则这个角的度数是( )
A.30° B.45° C.60° D.75°
4.如图, ,以 为一边作 ,则 的度数为( )
A. B.
C. 或 D. 或
5.如图,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD=150°,则∠BOC等于( )
A.30° B.45° C.50° D.60°
6.如图,小明在操场上从A点出发,先沿南偏东30°方向走到B点,再沿南偏东60°方向走到C点.这时,∠ABC的度数是( )
A.120° B.135° C.150° D.160°
7.如图,∠AOB=90°,OC平分∠AOB,OE平分∠AOD,若∠AOD=y°,则∠EOC的度数为( )
A. B. C. D.
8.如图,已知∠1=∠2,∠3=∠4,∠BOD= ∠AOB=90°.下列判断:①射线OF是∠BOE的角平分线;②∠DOE的补角是∠BOC;③∠AOC的余角只有∠COD;④∠DOE的余角有∠BOE和∠COD;⑤∠COD=∠BOE.其中正确的有( )
A.5个 B.4个 C.3个 D.2个
二、填空题
9.若一个角的补角是 ,则这个角的余角是 .
10.如图所示,两块三角板的直角顶点O重叠在一起,且OB恰好平分∠COD,则∠AOD的度数是 度.
11.如图,时钟显示时间为4:00,此时,时针与分针所成夹角为 度.
12.如图,点A,O,C在一条直线上,∠AOD=120°,且∠AOB:∠COD=3:5,则∠COD的度数为 ,∠BOC的度数为
13.如图,OB,OC是∠AOD的两条三等分线,则下列说法:①∠AOD = 3∠BOC;②∠AOD=2∠AOC;③∠AOC=2∠COD;④OC平分∠DOB.其中,不正确的是 (填序号).
三、解答题
14.如图,已知∠BAE=∠CAF=110°,∠CAE=60°,AD是∠BAF的角平分线,求∠BAD的度数.
15.已知∠AOB=50°,过点O引射线OC,若∠AOC:∠BOC=2:3,OD平分∠AOB,求∠COD的度数.
16.如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
17.如图,∠AOB=90°,∠AOC为∠AOB外的一个锐角,且∠AOC=30°,射线OM平分∠BOC,ON平分∠AOC.
(1)求∠MON的度数;
(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中∠AOC=β(β为锐角),其他条件不变,求∠MON的度数.
18.点C,D是半圆弧上的两个动点,在运动的过程中保持∠COD=80°.
(1)如图1,OM平分∠AOC,ON平分∠BOD,求∠MON的度数;
(2)如图2,若∠AOC=x°,OM平分∠AOD,ON平分∠BOC,求∠MON的度数.
参考答案
1.C
2.B
3.C
4.D
5.A
6.C
7.C
8.B
9.
10.135
11.120
12.60°;144°
13.②
14.解:由∠BAE=110°,∠CAE=60°,可得∠BAC=110°﹣60°=50°,结合∠CAF=110°,可得∠BAF=110°+50°=160°,再由AD平分∠BAF即可得∠BAD=80°.
试题解析:
∵∠BAE=110°,∠CAE=60°,
∴∠BAC=110°﹣60°=50°,
又∵∠CAF=110°,
∴∠BAF=110°+50°=160°,
又∵AD是∠BAF的角平分线,
∴∠BAD= ∠BAF= ×160°=80°.
15.解:分两种情况讨论:
( 1 )射线OC在∠AOB的内部,如图①;
设∠AOC=2x,则∠COB=3x,则2x+3x=50°,∴x=10°,∠AOC=2x=20°,∠AOD 50°=25°,∴∠COD=∠AOD﹣∠AOC=25°﹣20°=5°;
( 2 )射线OC在∠AOB的外部,如图②.
设∠AOC=2x,则∠COB=3x,则∠AOB=3x﹣2x=x=50°,∴∠AOC=2x=100°
∠AOD=25°,∴∠COD=∠AOC+∠AOD=100°+25°=125°.
综上所述:∠COD=5°或∠COD=125°.
16.(1)解:∵OA平分∠EOC,
∴∠AOC= ∠EOC= ×70°=35°,
∴∠BOD=∠AOC=35°
(2)解:设∠EOC=2x,∠EOD=3x,根据题意得2x+3x=180°,解得x=36°,
∴∠EOC=2x=72°,
∴∠AOC= ∠EOC= ×72°=36°,
∴∠BOD=∠AOC=36°
17.(1)解:∵∠AOB=90°,∠AOC=30°,
∴∠BOC=120°.
∵OM平分∠BOC,ON平分∠AOC,
∴∠COM=60°,∠CON=15°,
∴∠MON=∠COM﹣∠CON=45°
(2)解:∵∠AOB=α,∠AOC=30°,
∴∠BOC=α+30°.
∵OM平分∠BOC,ON平分∠AOC,
∴∠COM= α+15°,∠CON=15°,
∴∠MON=∠COM﹣∠CON= α
(3)解:∵∠AOB=90°,∠AOC=β,
∴∠BOC=90°+β.
∵OM平分∠BOC,ON平分∠AOC,
∴∠COM=45°+ β,∠CON= β,
∴∠MON=∠COM﹣∠CON=45°
18.(1)解;如图1,
∵OM平分∠AOC,ON平分∠BOD,
∴∠MOC= ∠AOC,∠NOD= ∠BOD,
又∵∠COD=80°,
∴∠AOC+∠BOD=100°﹣80°=100°,
∴∠MON=∠COD+∠MOC+∠NOD=80°+ ×100°=130°;
(2)解:如图2,∠AOC=x°,则∠AOD=x°+80°,∠BOD=100°﹣x°,
∵OM平分∠AOD
∴∠AOM= ∠AOD= x°+40°;
又∵ON平分∠BOC
∴∠BON= ∠BOC= (180°﹣x°)=90°﹣ x°,
∴∠MON=180°﹣(∠AOM+∠BON)=180°﹣( x°+40°+90°﹣ x°)
=180°﹣130°
=50°
