2023-2024学年人教版八年级 数学 上册 14.2.1平方差公式同步练习(无答案)
文档属性
| 名称 | 2023-2024学年人教版八年级 数学 上册 14.2.1平方差公式同步练习(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 142.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 00:00:00 | ||
图片预览

文档简介
14.2.1平方差公式
一、选择题。
1. 三个连续奇数,若中间一个数为n,则它们的积为( )
A. n3-4n B. n3+4n C. n3-n C.n3+n
2.下列各式不能用平方差公式计算的是( )
A. B.
C. D.
3.
A. B. C. D.
4.下列计算中,错误的有( )
①(3a+4)(3a-4)=9a2-4;
②(2a2-b)(2a2+b)=4a2-b2;
③(3-x)(x+3)=x2-9;
④(-x+y)·(x+y)=-(x-y)(x+y)=-x2-y2.
A.1个 B.2个 C.3个 D.4个
5.计算(a-b)(a+b)(a2+b2)(a4-b4)的结果是( )
A. B. C. D.
6.若(3b+a) ( )=a2﹣9b2,则括号内应填的代数式是( )
A.﹣a﹣3b B.a+3b C.﹣3b+a D.3b﹣a
7.计算:(1)×(1)×(1)×…×(1)×(1)的结果是( )
A. B. C. D.
8.计算的结果是( )
A. B. C. D.
9.为了运用平方差公式计算,下列变形正确的是( )
A. B.
C. D.
10.式子化简的结果为( )
A. B. C. D.
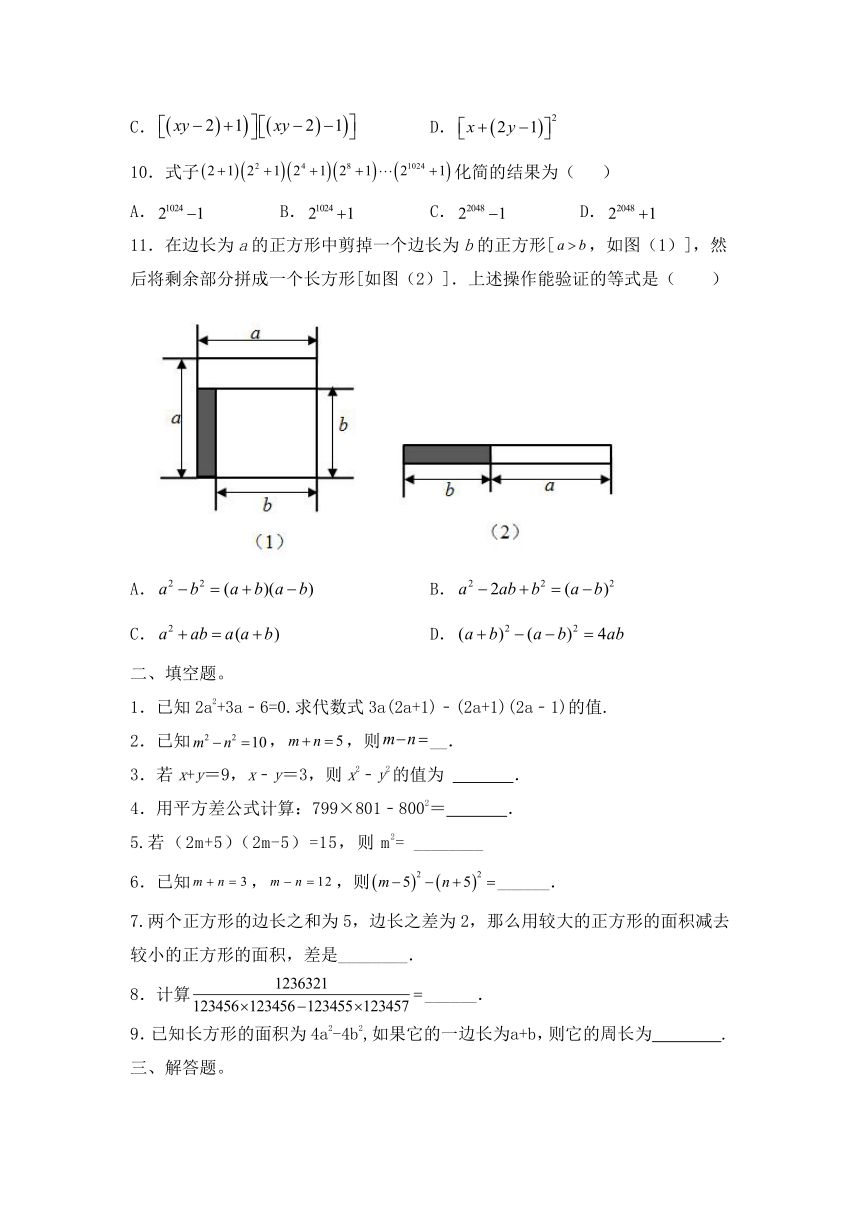
11.在边长为a的正方形中剪掉一个边长为b的正方形[,如图(1)],然后将剩余部分拼成一个长方形[如图(2)].上述操作能验证的等式是( )
A. B.
C. D.
二、填空题。
1.已知2a2+3a﹣6=0.求代数式3a(2a+1)﹣(2a+1)(2a﹣1)的值.
2.已知,,则__.
3.若x+y=9,x﹣y=3,则x2﹣y2的值为 .
4.用平方差公式计算:799×801﹣8002= .
5.若(2m+5)(2m-5)=15,则m2= ________
6.已知,,则______.
7.两个正方形的边长之和为5,边长之差为2,那么用较大的正方形的面积减去较小的正方形的面积,差是________.
8.计算______.
9.已知长方形的面积为4a2-4b2,如果它的一边长为a+b,则它的周长为 .
三、解答题。
1.计算:
(1)(x+2y)(2x﹣y)
(2)(2a﹣3b)(﹣2a﹣3b)
(3);
(4)6.98×512-492×6.98.
2.先化简,再求值
求的值,其中,.
3.已知2a2+3a﹣6=0.求代数式3a(2a+1)﹣(2a+1)(2a﹣1)的值.
4.对于任意实数、、、,我们规定符号的意义是按照这个规律计算:
(1)______
(2)当时,求的值.
5.小明将一个底面为正方形,高为 m 的无盖纸盒展成如图①所示的平面图形.
(1)请你计算无盖纸盒的表面展开图的面积(图中阴影部分的面积);
(2)将阴影部分拼成一个长方形,如图②所示,则这个长方形的长和宽是多少 面积又是多少
(3)比较(1)(2)的结果,你能得出什么结论
6.观察下列各式:
(x﹣1)(x+1)=x2﹣1;
(x﹣1)(x2+x+1)=x3﹣1;
(x﹣1)(x3+x2+x+1)=x4﹣1;
……
(1)根据以上规律,可知(x﹣1)(x7+x6+x5+x4+x3+x2+x+1)= ;
(2)你能否由此归纳出一般性规律:(x﹣1)(xn+xn﹣1+…+x+1)= ;
(3)根据(2)求出:1+2+22+23+…+22020+22021.
一、选择题。
1. 三个连续奇数,若中间一个数为n,则它们的积为( )
A. n3-4n B. n3+4n C. n3-n C.n3+n
2.下列各式不能用平方差公式计算的是( )
A. B.
C. D.
3.
A. B. C. D.
4.下列计算中,错误的有( )
①(3a+4)(3a-4)=9a2-4;
②(2a2-b)(2a2+b)=4a2-b2;
③(3-x)(x+3)=x2-9;
④(-x+y)·(x+y)=-(x-y)(x+y)=-x2-y2.
A.1个 B.2个 C.3个 D.4个
5.计算(a-b)(a+b)(a2+b2)(a4-b4)的结果是( )
A. B. C. D.
6.若(3b+a) ( )=a2﹣9b2,则括号内应填的代数式是( )
A.﹣a﹣3b B.a+3b C.﹣3b+a D.3b﹣a
7.计算:(1)×(1)×(1)×…×(1)×(1)的结果是( )
A. B. C. D.
8.计算的结果是( )
A. B. C. D.
9.为了运用平方差公式计算,下列变形正确的是( )
A. B.
C. D.
10.式子化简的结果为( )
A. B. C. D.
11.在边长为a的正方形中剪掉一个边长为b的正方形[,如图(1)],然后将剩余部分拼成一个长方形[如图(2)].上述操作能验证的等式是( )
A. B.
C. D.
二、填空题。
1.已知2a2+3a﹣6=0.求代数式3a(2a+1)﹣(2a+1)(2a﹣1)的值.
2.已知,,则__.
3.若x+y=9,x﹣y=3,则x2﹣y2的值为 .
4.用平方差公式计算:799×801﹣8002= .
5.若(2m+5)(2m-5)=15,则m2= ________
6.已知,,则______.
7.两个正方形的边长之和为5,边长之差为2,那么用较大的正方形的面积减去较小的正方形的面积,差是________.
8.计算______.
9.已知长方形的面积为4a2-4b2,如果它的一边长为a+b,则它的周长为 .
三、解答题。
1.计算:
(1)(x+2y)(2x﹣y)
(2)(2a﹣3b)(﹣2a﹣3b)
(3);
(4)6.98×512-492×6.98.
2.先化简,再求值
求的值,其中,.
3.已知2a2+3a﹣6=0.求代数式3a(2a+1)﹣(2a+1)(2a﹣1)的值.
4.对于任意实数、、、,我们规定符号的意义是按照这个规律计算:
(1)______
(2)当时,求的值.
5.小明将一个底面为正方形,高为 m 的无盖纸盒展成如图①所示的平面图形.
(1)请你计算无盖纸盒的表面展开图的面积(图中阴影部分的面积);
(2)将阴影部分拼成一个长方形,如图②所示,则这个长方形的长和宽是多少 面积又是多少
(3)比较(1)(2)的结果,你能得出什么结论
6.观察下列各式:
(x﹣1)(x+1)=x2﹣1;
(x﹣1)(x2+x+1)=x3﹣1;
(x﹣1)(x3+x2+x+1)=x4﹣1;
……
(1)根据以上规律,可知(x﹣1)(x7+x6+x5+x4+x3+x2+x+1)= ;
(2)你能否由此归纳出一般性规律:(x﹣1)(xn+xn﹣1+…+x+1)= ;
(3)根据(2)求出:1+2+22+23+…+22020+22021.
