陕西省渭南市尚德中学2024届高三上学期期中考试文科数学试卷(含答案)
文档属性
| 名称 | 陕西省渭南市尚德中学2024届高三上学期期中考试文科数学试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 510.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 12:20:59 | ||
图片预览




文档简介
尚德中学2024届高三上学期期中考试文科数学试题
一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合,则( )
A. B. C. D.
2.在复平面内,复数z对应的点为,则( )
A. B. C. D.
3. 已知,则“”是“”的( ).
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分又不必要条件
4. 已知等差数列{an}的前n项和为Sn,且a2+a8=0,S11=33,则公差d的值为( )
A. 1 B. 2 C. 3 D. 4
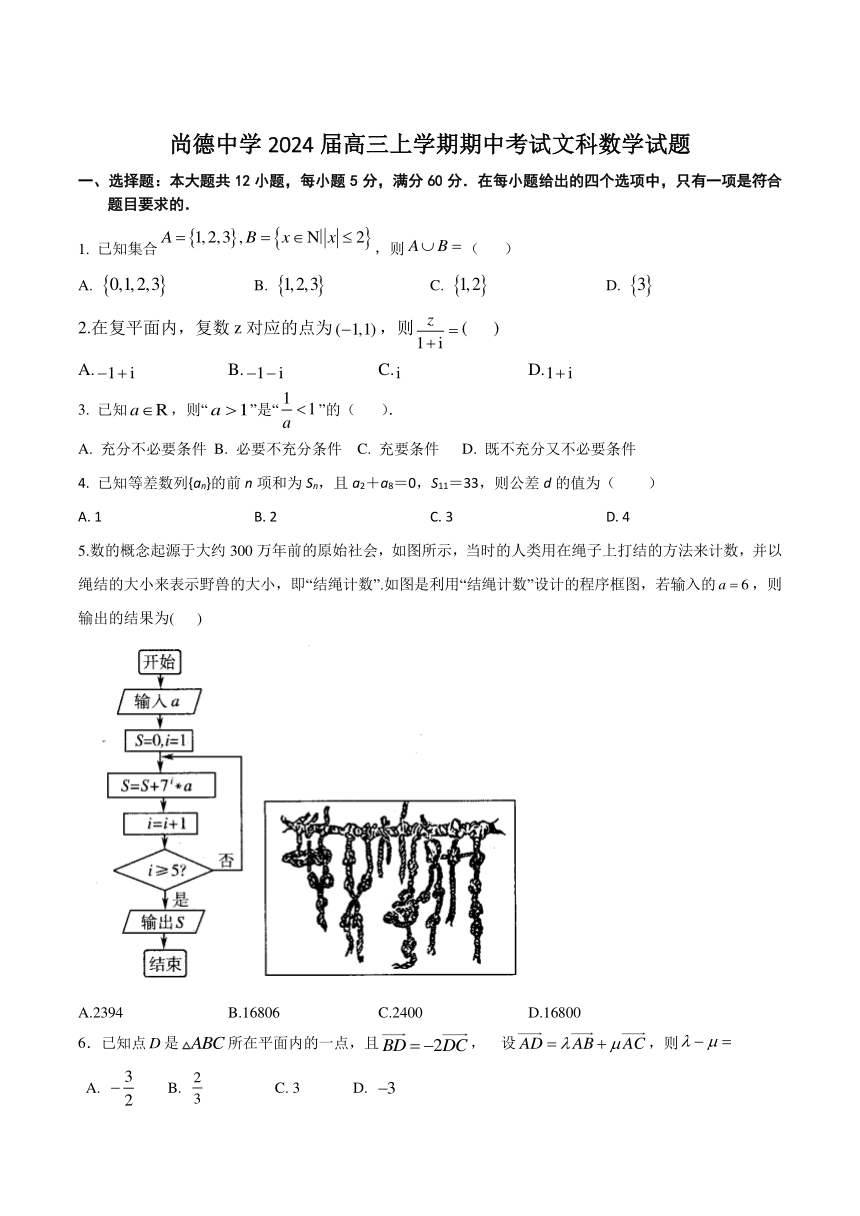
5.数的概念起源于大约300万年前的原始社会,如图所示,当时的人类用在绳子上打结的方法来计数,并以绳结的大小来表示野兽的大小,即“结绳计数”.如图是利用“结绳计数”设计的程序框图,若输入的,则输出的结果为( )
A.2394 B.16806 C.2400 D.16800
6.已知点是所在平面内的一点,且, 设,则
A. B. C. 3 D.
7.已知,,则( )
A. B. C. D.
8.已知函数的最小正周期为,将函数的图象向左平移个单位长度后得到的函数图象经过原点,则的最小值为( )
A. B. C. D.
9、已知在处取得极值,则的最小值为( )
A. B. C. 3 D. 9
10、在中,角的对边分别为,的面积为S,若,则的值是( )
A. B. C. D.
11.已知函数f(x)是定义域为(-∞,+∞)的奇函数, 满足f(1+x)=f(1-x), 若f(1)=2, 则f(1)+f(2)+f(3)+…+f(2023)= ( )
3 B、 0 C、 2023 D、 -2023
12、 设 m>0,对任意 恒成立, 则m 最大值( )
A.、 B、 e D、 e
二、填空题(本大题共4小题,每小题5分.共20分)
13.已知平面向量,,且,实数的值为 _____.
14.已知实数,满足则的最小值是______.
15. 设函数相邻两条对称轴之间的距离为,,则的最小值为__________.
16.已知数列的前项和为,数列的前项和为,满足,,且.若对任意,恒成立,则实数的最小值为 .
三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
17、已知是等差数列,是等比数列,且,,,.
(1)求的通项公式;
(2)设,求数列的前n项和.
18. 已知中内角A,,的对边分别为,,,向量,,为锐角且.
(1)求角的大小;
(2)如果,求的最大值.
19.(12分)
2014年7月18日15时,超强台风“威马逊”登陆海南省.据统计,本次台风造成全省直接经济损失119.52亿元.适逢暑假,小明调查住在自己小区的50户居民由于台风造成的经济损失,作出如下频率分布直方图:
经济损失 4000元以下 经济损失 4000元以上 合计
捐款超过500元 30
捐款低于500元 6
合计
(1)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如上表,在表格空白处填写正确数字,并说明是否有95%以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关?
(2)台风造成了小区多户居民门窗损坏,若小区所有居民的门窗均由李师傅和张师傅两人进行维修,李师傅每天早上在7:00到8:00之间的任意时刻来到小区,张师傅每天早上在7:30到8:30分之间的任意时刻来到小区,求李师傅比张师傅早到小区的概率.
附:临界值表
k0 2.072 2.706 3.841 5.024 6.635 7.879 10.828
P(K2≥k0) 0.15 0.10 0.05 0.025 0.010 0.005 0.001
参考公式:K2=,n=a+b+c+d.
20. 如图,在四棱锥中,已知平面平面ABCD,,,,AE是等边的中线.
(1)证明:平面.
(2)若,求点E到平面PBC的距离.
21、已知函数.
(1)求曲线在点处的切线方程;
(2)求证:.
选考题:共10分。请考生在第22、23两题中任选一题做答,如果多做,则按所做的第一题记分.
22. [选修4-4:极坐标与参数方程选讲]
在直角坐标系中,曲线的参数方程为(为参数).以原点为极点,
轴正半轴为极轴建立极坐标系,曲线的极坐标方程为.
(1)求曲线普通方程和的直角坐标方程;
(2)已知曲线的极坐标方程为,点是曲线与的交点,点是曲线与的交点,且均异于原点,且,求的值.
23.【选修4—5:不等式选讲】 已知函数.
(1)求不等式的解集;
(2)函数的最小值为m,正实数a,b,c满足,求证:.
参考答案:
1 A 2. C 3 A 4 C 5.D 6.D 7. C. 8. :C 9:C 10 C 11B 12 B
13 14 15 16.
17答案:(1)设的公比为q.
因为,,所以,所以.,
所以.
(2)由(1)知,所以.
设等差数列的公差为d.因为,所以,
所以.所以.因此.
从而数列的前项和
18解析:(1)∵,
∴,∴,
即.又∵为锐角,∴,
∴,∴.
(2)∵,,由余弦定理,
得.又,当且仅当时等号成立,
代入上式,得,故,
即的最大值为
19.解 (1)如下表:
经济损失4000元以下 经济损失4000元以上 合计
捐款超过500元 30 9 39
捐款低于500元 5 6 11
合计 35 15 50
K2=≈4.046>3.841.
所以有95%以上的把握认为捐款数额是否多于或少于500元和
自身经济损失是否到4000元有关.
(2)设李师傅、张师傅到小区的时间分别为x,y,则(x,y)可以看
成平面中的点.试验的全部结果所构成的区域为
Ω={(x,y)|7≤x≤8,7.5≤y≤8.5},则SΩ=1,事件A表示“李师傅比张师
傅早到小区”,所构成的区域为A={(x,y)|y≥x,7≤x≤8,7.5≤y≤8.5},
即图中的阴影部分面积为SA=1-××=,所以P(A)==,
19. 【小问1】
证明:如图,取PC的中点F,连接EF,BF.
因为E是棱PD的中点,所以,且.
因为,,所以,,
所以四边形ABFE是平行四边形,所以.
因为平面,平面,
所以平面.
【小问2】
解:如图,连接BD,因为E是PD的中点,所以点E到平面PBC的距离等于点D到平面PBC的距离的一半.
平面平面,,,易知平面PAD,平面PAD.
因此平面内的直线都与垂直,
因为,,所以,,
所以.
设D到平面PBC的距离为h,则.
又,三棱锥高即为的高,长为,
所以.
由,得,所以点E到平面PBC的距离等于.
21答案及解析:
答案:(1)定义域为,.
. .
所以曲线在处的切线方程为.即.
(2)记..
由解得.
与在区间上的情况如下:
x 1
0
↘ 极小 ↗
所以在时取得最小值.
所以.所以.
所以在上单调递增.
又由知,
当时,,,所以;
当时,,,所以.
所以.
22【解析】(1)由,
消去参数可得普通方程为,,
由,得曲线的直角坐标方程为;
(2)由(1)得曲线,由,
可得其极坐标方程为由题意设,,
则.
,,,.
23解析:(1)由题意可得:,
当时,则,解得;
当时,则,解得;
当时,则,解得;
综上所述:不等式的解集为.
(2)∵,当且仅当时等号成立,
∴函数的最小值为,则,
又∵,当且仅当,即时等号成立;
,当且仅当,即时等号成立;
,当且仅当,即时等号成立;
上式相加可得:,当且仅当时等号成立,
∴.
一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合,则( )
A. B. C. D.
2.在复平面内,复数z对应的点为,则( )
A. B. C. D.
3. 已知,则“”是“”的( ).
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分又不必要条件
4. 已知等差数列{an}的前n项和为Sn,且a2+a8=0,S11=33,则公差d的值为( )
A. 1 B. 2 C. 3 D. 4
5.数的概念起源于大约300万年前的原始社会,如图所示,当时的人类用在绳子上打结的方法来计数,并以绳结的大小来表示野兽的大小,即“结绳计数”.如图是利用“结绳计数”设计的程序框图,若输入的,则输出的结果为( )
A.2394 B.16806 C.2400 D.16800
6.已知点是所在平面内的一点,且, 设,则
A. B. C. 3 D.
7.已知,,则( )
A. B. C. D.
8.已知函数的最小正周期为,将函数的图象向左平移个单位长度后得到的函数图象经过原点,则的最小值为( )
A. B. C. D.
9、已知在处取得极值,则的最小值为( )
A. B. C. 3 D. 9
10、在中,角的对边分别为,的面积为S,若,则的值是( )
A. B. C. D.
11.已知函数f(x)是定义域为(-∞,+∞)的奇函数, 满足f(1+x)=f(1-x), 若f(1)=2, 则f(1)+f(2)+f(3)+…+f(2023)= ( )
3 B、 0 C、 2023 D、 -2023
12、 设 m>0,对任意 恒成立, 则m 最大值( )
A.、 B、 e D、 e
二、填空题(本大题共4小题,每小题5分.共20分)
13.已知平面向量,,且,实数的值为 _____.
14.已知实数,满足则的最小值是______.
15. 设函数相邻两条对称轴之间的距离为,,则的最小值为__________.
16.已知数列的前项和为,数列的前项和为,满足,,且.若对任意,恒成立,则实数的最小值为 .
三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
17、已知是等差数列,是等比数列,且,,,.
(1)求的通项公式;
(2)设,求数列的前n项和.
18. 已知中内角A,,的对边分别为,,,向量,,为锐角且.
(1)求角的大小;
(2)如果,求的最大值.
19.(12分)
2014年7月18日15时,超强台风“威马逊”登陆海南省.据统计,本次台风造成全省直接经济损失119.52亿元.适逢暑假,小明调查住在自己小区的50户居民由于台风造成的经济损失,作出如下频率分布直方图:
经济损失 4000元以下 经济损失 4000元以上 合计
捐款超过500元 30
捐款低于500元 6
合计
(1)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如上表,在表格空白处填写正确数字,并说明是否有95%以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关?
(2)台风造成了小区多户居民门窗损坏,若小区所有居民的门窗均由李师傅和张师傅两人进行维修,李师傅每天早上在7:00到8:00之间的任意时刻来到小区,张师傅每天早上在7:30到8:30分之间的任意时刻来到小区,求李师傅比张师傅早到小区的概率.
附:临界值表
k0 2.072 2.706 3.841 5.024 6.635 7.879 10.828
P(K2≥k0) 0.15 0.10 0.05 0.025 0.010 0.005 0.001
参考公式:K2=,n=a+b+c+d.
20. 如图,在四棱锥中,已知平面平面ABCD,,,,AE是等边的中线.
(1)证明:平面.
(2)若,求点E到平面PBC的距离.
21、已知函数.
(1)求曲线在点处的切线方程;
(2)求证:.
选考题:共10分。请考生在第22、23两题中任选一题做答,如果多做,则按所做的第一题记分.
22. [选修4-4:极坐标与参数方程选讲]
在直角坐标系中,曲线的参数方程为(为参数).以原点为极点,
轴正半轴为极轴建立极坐标系,曲线的极坐标方程为.
(1)求曲线普通方程和的直角坐标方程;
(2)已知曲线的极坐标方程为,点是曲线与的交点,点是曲线与的交点,且均异于原点,且,求的值.
23.【选修4—5:不等式选讲】 已知函数.
(1)求不等式的解集;
(2)函数的最小值为m,正实数a,b,c满足,求证:.
参考答案:
1 A 2. C 3 A 4 C 5.D 6.D 7. C. 8. :C 9:C 10 C 11B 12 B
13 14 15 16.
17答案:(1)设的公比为q.
因为,,所以,所以.,
所以.
(2)由(1)知,所以.
设等差数列的公差为d.因为,所以,
所以.所以.因此.
从而数列的前项和
18解析:(1)∵,
∴,∴,
即.又∵为锐角,∴,
∴,∴.
(2)∵,,由余弦定理,
得.又,当且仅当时等号成立,
代入上式,得,故,
即的最大值为
19.解 (1)如下表:
经济损失4000元以下 经济损失4000元以上 合计
捐款超过500元 30 9 39
捐款低于500元 5 6 11
合计 35 15 50
K2=≈4.046>3.841.
所以有95%以上的把握认为捐款数额是否多于或少于500元和
自身经济损失是否到4000元有关.
(2)设李师傅、张师傅到小区的时间分别为x,y,则(x,y)可以看
成平面中的点.试验的全部结果所构成的区域为
Ω={(x,y)|7≤x≤8,7.5≤y≤8.5},则SΩ=1,事件A表示“李师傅比张师
傅早到小区”,所构成的区域为A={(x,y)|y≥x,7≤x≤8,7.5≤y≤8.5},
即图中的阴影部分面积为SA=1-××=,所以P(A)==,
19. 【小问1】
证明:如图,取PC的中点F,连接EF,BF.
因为E是棱PD的中点,所以,且.
因为,,所以,,
所以四边形ABFE是平行四边形,所以.
因为平面,平面,
所以平面.
【小问2】
解:如图,连接BD,因为E是PD的中点,所以点E到平面PBC的距离等于点D到平面PBC的距离的一半.
平面平面,,,易知平面PAD,平面PAD.
因此平面内的直线都与垂直,
因为,,所以,,
所以.
设D到平面PBC的距离为h,则.
又,三棱锥高即为的高,长为,
所以.
由,得,所以点E到平面PBC的距离等于.
21答案及解析:
答案:(1)定义域为,.
. .
所以曲线在处的切线方程为.即.
(2)记..
由解得.
与在区间上的情况如下:
x 1
0
↘ 极小 ↗
所以在时取得最小值.
所以.所以.
所以在上单调递增.
又由知,
当时,,,所以;
当时,,,所以.
所以.
22【解析】(1)由,
消去参数可得普通方程为,,
由,得曲线的直角坐标方程为;
(2)由(1)得曲线,由,
可得其极坐标方程为由题意设,,
则.
,,,.
23解析:(1)由题意可得:,
当时,则,解得;
当时,则,解得;
当时,则,解得;
综上所述:不等式的解集为.
(2)∵,当且仅当时等号成立,
∴函数的最小值为,则,
又∵,当且仅当,即时等号成立;
,当且仅当,即时等号成立;
,当且仅当,即时等号成立;
上式相加可得:,当且仅当时等号成立,
∴.
同课章节目录
