专题5.3 平行线的性质【十大题型】(举一反三)(华东师大版)(原卷版)(无答案)
文档属性
| 名称 | 专题5.3 平行线的性质【十大题型】(举一反三)(华东师大版)(原卷版)(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 21:37:33 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
专题5.3 平行线的性质【十大题型】
【华东师大版】
TOC \o "1-3" \h \u
HYPERLINK \l "_Toc4766" 【题型1 由平行线的性质求角度】 1
HYPERLINK \l "_Toc31178" 【题型2 由平行线的性质解决折叠问题】 2
HYPERLINK \l "_Toc9329" 【题型3 平行线性质的实际应用】 4
HYPERLINK \l "_Toc3945" 【题型4 由平行线的判定与性质进行证明】 5
HYPERLINK \l "_Toc11118" 【题型5 由平行线的判定与性质进行计算】 7
HYPERLINK \l "_Toc10120" 【题型6 由平行线的判定与性质探究角度之间的关系】 8
HYPERLINK \l "_Toc19950" 【题型7 由平行线的判定与性质确定角度定值问题】 10
HYPERLINK \l "_Toc10508" 【题型8 由平行线的判定与性质探究规律问题】 11
HYPERLINK \l "_Toc4463" 【题型9 由平行线的判定与性质解决三角尺问题】 13
HYPERLINK \l "_Toc32001" 【题型10 由平行线的判定与性质解决旋转问题】 14
【知识点 平行线的性质】
1. 两条平行被第三条直线所截同位角相等.简单说成两直线平行同位角相等.
2. 两条平行线被第三条直线所截内错角相等.简单说成两直线平行内错角相等.
3. 两条平行线被第三条直线所截同旁内角互补.简单说成两直线平行同旁内角互补.
【题型1 由平行线的性质求角度】
【例1】(2023下·福建厦门·七年级校考期中)如图,,平分,,,,则下列结论:①;②平分;③;④.其中正确的有 .
【变式1-1】(2023上·重庆沙坪坝·七年级重庆八中校考期中)如图所示,已知,点在线段上(不与点、点重合),连接,若,.则的值为( )
A. B. C. D.
【变式1-2】(2023下·陕西西安·七年级校考期末)如图,已知,点是射线上一动点(与不重合),、分别平分和,交射线于,(推理时不需要写出每一步的理由)
(1)求的度数.
(2)当点运动时,那么的度数比值是否随之发生变化?若不变,请求出这个比值;若变化,请找出变化规律.
【变式1-3】(2023上·陕西渭南·七年级统考期中)在中,点D是延长线上的一点,过点D作,和的平分线交于点G.
(1)如图1,若,求出的度数;
(2)如图2,若,试判断与的数量关系,并证明你的结论.
【题型2 由平行线的性质解决折叠问题】
【例2】(2023下·山东青岛·七年级统考期中)按如图方式折叠一张对边互相平行的纸条,是折痕,若,则以下结论正确的是( )
①;②;③;④
A.①③ B.②④ C.①③④ D.②③④
【变式2-1】(2023上·福建福州·七年级期中)如图,在中,,将沿折叠得到,则的度数为 °.
【变式2-2】(2023下·广东佛山·七年级校考期中)如图,已知长方形纸片,点E,F在边上,点G,H在边上,分别沿,折叠,使点D和点A都落在点M处,若,则的度数为( )
A. B. C. D.
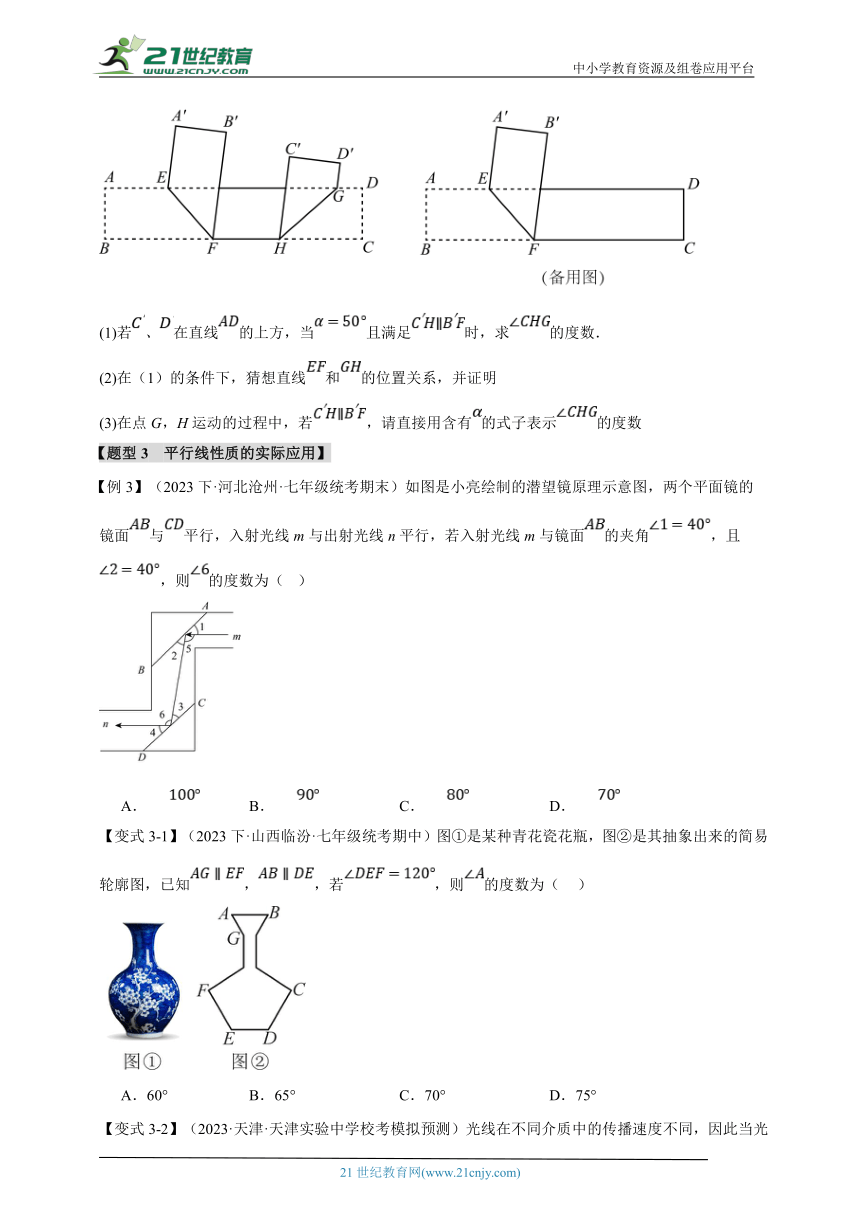
【变式2-3】(2023下·浙江台州·七年级统考期末)如图,有一张长方形纸条,,在线段,上分别取点G,H,将四边形沿直线折叠,点C,D的对应点为,,将四边形沿直线折叠,点A,B的对应点为,,设.
(1)若、在直线的上方,当且满足时,求的度数.
(2)在(1)的条件下,猜想直线和的位置关系,并证明
(3)在点G,H运动的过程中,若,请直接用含有的式子表示的度数
【题型3 平行线性质的实际应用】
【例3】(2023下·河北沧州·七年级统考期末)如图是小亮绘制的潜望镜原理示意图,两个平面镜的镜面与平行,入射光线m与出射光线n平行,若入射光线m与镜面的夹角,且,则的度数为( )
A. B. C. D.
【变式3-1】(2023下·山西临汾·七年级统考期中)图①是某种青花瓷花瓶,图②是其抽象出来的简易轮廓图,已知,,若,则的度数为( )
A.60° B.65° C.70° D.75°
【变式3-2】(2023·天津·天津实验中学校考模拟预测)光线在不同介质中的传播速度不同,因此当光线从水中射向空气时,要发生折射,如图,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.若水面和杯底是互相平行的,且,,则 , .
【变式3-3】(2023下·吉林松原·七年级统考期中)如图1,为响应国家新能源建设,公交站亭装上了太阳能电池板.当地某一季节的太阳光(平行光线),如图2,电池板与最大夹角时刻的太阳光线相垂直,要使,需将电池板逆时针旋转度, .
【题型4 由平行线的判定与性质进行证明】
【例4】(2023上·黑龙江哈尔滨·七年级哈尔滨风华中学校考期中)完成下面的证明:
如图,已知,,,求证:.
证明:,
______(__________),
,
______(__________).
即,
,
,
______,
______(__________).
又,
(__________).
【变式4-1】(2023下·山东潍坊·七年级阶段练习)如图所示,已知,平分,与相交于点,,试证明:.
【变式4-2】(2023下·贵州遵义·七年级校联考期中)如图,点A、D、E、F四点共线,已知,,求证:.完善下面的解答过程.
证明:因为(已知),
所以 ( ),
所以( ),
因为(已知),
所以 ,
所以,
所以,( )
即:,
因为(已知),
所以,
即:,
因此( ).
【变式4-3】(2023下·辽宁大连·七年级统考期末)如图,.用等式表示与的数量关系,并证明.
【题型5 由平行线的判定与性质进行计算】
【例5】(2023下·山西吕梁·七年级统考期中)综合与实践
如图,三角形中,,,.将三角形向右平移得到三角尺.分别连接,,.
(1)线段与的数量关系和位置关系是:____________,其依据是____________;
(2)求证:;
(3)猜想与的数量关系,并说明理由.
【变式5-1】(2023上·黑龙江哈尔滨·七年级哈尔滨市萧红中学校考期中)如图,已知,,点在射线上,且,则的度数为 .
【变式5-2】(2023上·安徽合肥·七年级校考期中)如图,在中,点D在上,点在上,交于F.已知交于,平分,交于H.
(1)求的度数.
(2)若,,求的度数.
【变式5-3】(2023下·江苏泰州·七年级校考期中)如图,在中,点、在边上,点在边上,点在边上,与的延长线交于点,,.
(1)与平行吗?为什么?
(2)若,求的度数.
【题型6 由平行线的判定与性质探究角度之间的关系】
【例6】(2023下·河北石家庄·七年级石家庄市藁城区第一中学校联考期中)如图,直线,直线和直线分别交于两点,点分别在直线上,点在直线上,连接.
(1)猜想:如图1,若点在线段上,,,则_____________;
(2)探究:如图1,若点在线段上,写出,,之间的数量关系并说明理由;
(3)拓展:如图2,若点在射线上或在射线上时,写出,,之间的数量关系并说明理由.
【变式6-1】(2023下·四川宜宾·七年级统考期末)如图,将线段平移至,使点A与点D对应,点B与点C对应,连接,.E为延长线上一点,连接,,且,作平分交于点F.
(1)若当时,求的度数;
(2)若,试探究与之间的数量关系,并说明理由.
【变式6-2】(2023下·上海静安·七年级上海市市北初级中学校考期中)已知:四边形,(如图1),点P在直线上运动,点P和点C,D不重合,点P,A,B不在同一条直线上,若记,,分别为,,.
(1)如图2,当点P在线段上运动时,写出,,之间的关系并说出理由.
(2)如果点P在线段的延长线上运动,探究,,之间的关系,并说明理由.
【变式6-3】(2023下·河南焦作·七年级统考期中)如图1,已知,C为射线上一点(不与点A 重合),连接
【发现】如图2过点C作
(1)若,求 的度数;
(2)若,求的度数;
【探究】直接写出图1中和之间的数量关系: ;
【拓展】利用【探究】中的结论完成下列问题.
如图3,为射线上一点(不与点A 重合),在射线上取一点O,过点O作直线,使,平分交于点E,平分交于点F,交于点G,当点C沿着射线方向运动时,的度数是否会变化 ?若变化,请说明理由;若不变,请求出这个不变的值.
【题型7 由平行线的判定与性质确定角度定值问题】
【例7】(2023下·湖北十堰·七年级校考期中)如图,已知,,点是射线上一动点(与点不重合),,分别平分和,交射线于点,.
(1)__________;
(2)当点运动时,是否为定值?若是定值,请求出这个定值;若不是,请说明理由;
(3)当点运动到使时,求的度数.
【变式7-1】(2023下·四川达州·七年级统考期末)已知直线,点E、F分别在直线、上,连接,平分.
(1)如图1,连接,若平分.求的度数;
(2)如图2,连接,若,猜想和的数量关系,并说明理由;
(3)如图3,点H为线段(端点除外)上的一个动点,过点H作的垂线交于M,连接,若平分,问的度数是否为定值?若是,求出的度数;若不是,请说明理由.
【变式7-2】(2023下·山东济南·七年级统考期中)如图①,,点A,C分别在射线FE和FH上,.
(1)若,则的度数为______;
(2)小明同学发现,无论如何变化,的值始终为定值,并给出了一种证明该发现的辅助线作法:如图②,过点A作,交CD于点M.请你根据小明同学提供的辅助线,确定该定值,并说明理由;
(3)如图③,把“”改为“”,其他条件保持不变,猜想与的数量关系,并说明理由.
【变式7-3】(2023下·福建龙岩·七年级统考期末)如图1,点A、D分别在射线BM、CN线上,BM∥CN,BM⊥BC于点B,AE平分∠BAD交BC于点E,连接DE,∠1+∠2=90°.
(1)求证:AE⊥ED;
(2)求证:DE平分∠ADC;
(3)如图2,∠EAM和∠EDN的平分线交于点F,试猜想∠F的值是否为定值,若是,请予以证明;若不是,请说明理由.
【题型8 由平行线的判定与性质探究规律问题】
【例8】(2023下·四川成都·七年级树德中学校考阶段练习)(1)如图①,已知,图中,,之间有什么关系?
(2)如图②,已知,图中,,,之间有什么关系?
(3)如图③,已知,请直接写出图中,,,,之间的关系
(4)通过以上3个问题,你发现了什么规律?
【变式8-1】(2023上·广东江门·七年级江门市福泉奥林匹克学校校考阶段练习)如图,已知直线被直线所截,且,,分别平分,,,分别平分和,,分别平分,…依次规律,得点,则的度数为 .
【变式8-2】(2023下·河南郑州·七年级郑州外国语中学校考期中)在小学我们学过三角形的内角和等于;科学实验又证明,平面镜反射光线的规律是射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等.例如:在图①、图②中,都有,.设镜子与的夹角.
(1)如图①,若,,则_________;
(2)如图②,若,入射光线与反射光线的夹角.求的度数;
(3)如图③,若,设镜子与的夹角,入射光线与镜面的夹角,已知入射光线从镜面反射到镜面,再反射到镜面,最后经镜面反射后,当反射光线与入射光线平行时,探索与的数量关系,并说明理由.
【变式8-3】(2023上·广东广州·七年级广州市黄埔军校纪念中学校考开学考试)如图①所示,四边形为一张长方形纸片.如图②所示,将长方形纸片剪两刀,剪出三个角(、、),则 (度);
(1)如图③所示,将长方形纸片剪三刀,剪出四个角(、、、),则 (度);
(2)如图④所示,将长方形纸片剪四刀,剪出五个角(、、、、),则 (度);
(3)根据前面的探索规律,将本题按照上述剪法剪刀,剪出个角,那么这个角的和是 (度).
【题型9 由平行线的判定与性质解决三角尺问题】
【例9】(2023下·湖北孝感·七年级统考期末)将一副三角尺的直角顶点重合按如图放置,其中,,,.有下列结论:
(1)与互为补角;
(2)若,则;
(3)若,则;
(4)若,则.
其中正确的结论个数有( )
A.1个 B.2个 C.3个 D.4个
【变式9-1】(2023上·河南郑州·七年级校考期末)一副三角尺如图所示摆放,∠α 的大小为( )度
A.90 B.100 C.105 D.120
【变式9-2】(2023下·云南玉溪·七年级统考期末)含的三角板和含的三角板如图摆放,若,,,则的度数是( )
A. B. C. D.
【变式9-3】(2023下·贵州六盘水·七年级统考期末)如图,,将两块直角三角尺(一块含30°,一块含45°)按如下方式进行摆放,恰好满足,.
(1)求的度数;
(2)试判断与的位置关系,并说明理由.
【题型10 由平行线的判定与性质解决旋转问题】
【例10】(2023上·山西太原·七年级校考期末)问题情境:如图1,将含 角的三角板 和含角的三角板 叠放在一起,使直角顶点重合,点 D 落在直线 上,点 E 落在直线 上. 绕点 A 旋转, 边 与 、 分别相交与点 F、点N,边 与 相交于点 M.
(1)如图 2,当 时:
①求的度数.
②判断 与的数量关系,并说明理由.
(2)如图 3,当 平分 时:
①求的度数;
②判断 与 的位置关系,并说明理由.
【变式10-1】(2023下·重庆·七年级西南大学附中校考期中)如图,△OAB为等腰直角三角形(∠A=∠B=45°,∠AOB=90°),△OCD为等边三角形(∠C=∠D=∠COD=60°),满足OC>OA,△OCD绕点O从射线OC与射线OA重合的位置开始,逆时针旋转,旋转的角度为α(0°<α<360°),下列说法错误的是( )
A.当α=15°时,DC∥AB
B.当OC⊥AB时,α=45°
C.当边OB与边OD在同一直线上时,直线DC与直线AB相交形成的锐角为15°
D.整个旋转过程,共有10个位置使得△OAB与△OCD有一条边平行
【变式10-2】(2023下·四川成都·七年级校考期中)“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了A,D两座可旋转探照灯.假定主道路是平行的,即,,为上两点,平分交于点,为上一点,连接,平分交于点.
(1)若,则 ;
(2)作交于点,且满足,当时,试说明:;
(3)在(1)问的条件下,探照灯A、D照出的光线在铁路所在平面旋转,探照灯射出的光线以每秒5度的速度逆时针转动,探照灯射出的光线以每秒15度的速度逆时针转动,转至射线后立即以相同速度回转,若它们同时开始转动,设转动时间为秒,当回到出发时的位置时同时停止转动,则在转动过程中,当与互相平行或垂直时,请直接写出此时t的值.
【变式10-3】(2023下·湖北武汉·七年级统考期末)已知直线与直线、分别交于、两点,和的角平分线交于点,且.
(1)求证:;
(2)如图,和的角平分线交于点,求的度数;
(3)如图,若,延长线段得射线,延长线段得射线,射线绕点以每秒15°的速度逆时针旋转360°后停止,射线绕点以每秒3°的速度顺时针旋转180°以后停止.设它们同时旋转秒,问为多少时,射线,直接写出的值______秒.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
专题5.3 平行线的性质【十大题型】
【华东师大版】
TOC \o "1-3" \h \u
HYPERLINK \l "_Toc4766" 【题型1 由平行线的性质求角度】 1
HYPERLINK \l "_Toc31178" 【题型2 由平行线的性质解决折叠问题】 2
HYPERLINK \l "_Toc9329" 【题型3 平行线性质的实际应用】 4
HYPERLINK \l "_Toc3945" 【题型4 由平行线的判定与性质进行证明】 5
HYPERLINK \l "_Toc11118" 【题型5 由平行线的判定与性质进行计算】 7
HYPERLINK \l "_Toc10120" 【题型6 由平行线的判定与性质探究角度之间的关系】 8
HYPERLINK \l "_Toc19950" 【题型7 由平行线的判定与性质确定角度定值问题】 10
HYPERLINK \l "_Toc10508" 【题型8 由平行线的判定与性质探究规律问题】 11
HYPERLINK \l "_Toc4463" 【题型9 由平行线的判定与性质解决三角尺问题】 13
HYPERLINK \l "_Toc32001" 【题型10 由平行线的判定与性质解决旋转问题】 14
【知识点 平行线的性质】
1. 两条平行被第三条直线所截同位角相等.简单说成两直线平行同位角相等.
2. 两条平行线被第三条直线所截内错角相等.简单说成两直线平行内错角相等.
3. 两条平行线被第三条直线所截同旁内角互补.简单说成两直线平行同旁内角互补.
【题型1 由平行线的性质求角度】
【例1】(2023下·福建厦门·七年级校考期中)如图,,平分,,,,则下列结论:①;②平分;③;④.其中正确的有 .
【变式1-1】(2023上·重庆沙坪坝·七年级重庆八中校考期中)如图所示,已知,点在线段上(不与点、点重合),连接,若,.则的值为( )
A. B. C. D.
【变式1-2】(2023下·陕西西安·七年级校考期末)如图,已知,点是射线上一动点(与不重合),、分别平分和,交射线于,(推理时不需要写出每一步的理由)
(1)求的度数.
(2)当点运动时,那么的度数比值是否随之发生变化?若不变,请求出这个比值;若变化,请找出变化规律.
【变式1-3】(2023上·陕西渭南·七年级统考期中)在中,点D是延长线上的一点,过点D作,和的平分线交于点G.
(1)如图1,若,求出的度数;
(2)如图2,若,试判断与的数量关系,并证明你的结论.
【题型2 由平行线的性质解决折叠问题】
【例2】(2023下·山东青岛·七年级统考期中)按如图方式折叠一张对边互相平行的纸条,是折痕,若,则以下结论正确的是( )
①;②;③;④
A.①③ B.②④ C.①③④ D.②③④
【变式2-1】(2023上·福建福州·七年级期中)如图,在中,,将沿折叠得到,则的度数为 °.
【变式2-2】(2023下·广东佛山·七年级校考期中)如图,已知长方形纸片,点E,F在边上,点G,H在边上,分别沿,折叠,使点D和点A都落在点M处,若,则的度数为( )
A. B. C. D.
【变式2-3】(2023下·浙江台州·七年级统考期末)如图,有一张长方形纸条,,在线段,上分别取点G,H,将四边形沿直线折叠,点C,D的对应点为,,将四边形沿直线折叠,点A,B的对应点为,,设.
(1)若、在直线的上方,当且满足时,求的度数.
(2)在(1)的条件下,猜想直线和的位置关系,并证明
(3)在点G,H运动的过程中,若,请直接用含有的式子表示的度数
【题型3 平行线性质的实际应用】
【例3】(2023下·河北沧州·七年级统考期末)如图是小亮绘制的潜望镜原理示意图,两个平面镜的镜面与平行,入射光线m与出射光线n平行,若入射光线m与镜面的夹角,且,则的度数为( )
A. B. C. D.
【变式3-1】(2023下·山西临汾·七年级统考期中)图①是某种青花瓷花瓶,图②是其抽象出来的简易轮廓图,已知,,若,则的度数为( )
A.60° B.65° C.70° D.75°
【变式3-2】(2023·天津·天津实验中学校考模拟预测)光线在不同介质中的传播速度不同,因此当光线从水中射向空气时,要发生折射,如图,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.若水面和杯底是互相平行的,且,,则 , .
【变式3-3】(2023下·吉林松原·七年级统考期中)如图1,为响应国家新能源建设,公交站亭装上了太阳能电池板.当地某一季节的太阳光(平行光线),如图2,电池板与最大夹角时刻的太阳光线相垂直,要使,需将电池板逆时针旋转度, .
【题型4 由平行线的判定与性质进行证明】
【例4】(2023上·黑龙江哈尔滨·七年级哈尔滨风华中学校考期中)完成下面的证明:
如图,已知,,,求证:.
证明:,
______(__________),
,
______(__________).
即,
,
,
______,
______(__________).
又,
(__________).
【变式4-1】(2023下·山东潍坊·七年级阶段练习)如图所示,已知,平分,与相交于点,,试证明:.
【变式4-2】(2023下·贵州遵义·七年级校联考期中)如图,点A、D、E、F四点共线,已知,,求证:.完善下面的解答过程.
证明:因为(已知),
所以 ( ),
所以( ),
因为(已知),
所以 ,
所以,
所以,( )
即:,
因为(已知),
所以,
即:,
因此( ).
【变式4-3】(2023下·辽宁大连·七年级统考期末)如图,.用等式表示与的数量关系,并证明.
【题型5 由平行线的判定与性质进行计算】
【例5】(2023下·山西吕梁·七年级统考期中)综合与实践
如图,三角形中,,,.将三角形向右平移得到三角尺.分别连接,,.
(1)线段与的数量关系和位置关系是:____________,其依据是____________;
(2)求证:;
(3)猜想与的数量关系,并说明理由.
【变式5-1】(2023上·黑龙江哈尔滨·七年级哈尔滨市萧红中学校考期中)如图,已知,,点在射线上,且,则的度数为 .
【变式5-2】(2023上·安徽合肥·七年级校考期中)如图,在中,点D在上,点在上,交于F.已知交于,平分,交于H.
(1)求的度数.
(2)若,,求的度数.
【变式5-3】(2023下·江苏泰州·七年级校考期中)如图,在中,点、在边上,点在边上,点在边上,与的延长线交于点,,.
(1)与平行吗?为什么?
(2)若,求的度数.
【题型6 由平行线的判定与性质探究角度之间的关系】
【例6】(2023下·河北石家庄·七年级石家庄市藁城区第一中学校联考期中)如图,直线,直线和直线分别交于两点,点分别在直线上,点在直线上,连接.
(1)猜想:如图1,若点在线段上,,,则_____________;
(2)探究:如图1,若点在线段上,写出,,之间的数量关系并说明理由;
(3)拓展:如图2,若点在射线上或在射线上时,写出,,之间的数量关系并说明理由.
【变式6-1】(2023下·四川宜宾·七年级统考期末)如图,将线段平移至,使点A与点D对应,点B与点C对应,连接,.E为延长线上一点,连接,,且,作平分交于点F.
(1)若当时,求的度数;
(2)若,试探究与之间的数量关系,并说明理由.
【变式6-2】(2023下·上海静安·七年级上海市市北初级中学校考期中)已知:四边形,(如图1),点P在直线上运动,点P和点C,D不重合,点P,A,B不在同一条直线上,若记,,分别为,,.
(1)如图2,当点P在线段上运动时,写出,,之间的关系并说出理由.
(2)如果点P在线段的延长线上运动,探究,,之间的关系,并说明理由.
【变式6-3】(2023下·河南焦作·七年级统考期中)如图1,已知,C为射线上一点(不与点A 重合),连接
【发现】如图2过点C作
(1)若,求 的度数;
(2)若,求的度数;
【探究】直接写出图1中和之间的数量关系: ;
【拓展】利用【探究】中的结论完成下列问题.
如图3,为射线上一点(不与点A 重合),在射线上取一点O,过点O作直线,使,平分交于点E,平分交于点F,交于点G,当点C沿着射线方向运动时,的度数是否会变化 ?若变化,请说明理由;若不变,请求出这个不变的值.
【题型7 由平行线的判定与性质确定角度定值问题】
【例7】(2023下·湖北十堰·七年级校考期中)如图,已知,,点是射线上一动点(与点不重合),,分别平分和,交射线于点,.
(1)__________;
(2)当点运动时,是否为定值?若是定值,请求出这个定值;若不是,请说明理由;
(3)当点运动到使时,求的度数.
【变式7-1】(2023下·四川达州·七年级统考期末)已知直线,点E、F分别在直线、上,连接,平分.
(1)如图1,连接,若平分.求的度数;
(2)如图2,连接,若,猜想和的数量关系,并说明理由;
(3)如图3,点H为线段(端点除外)上的一个动点,过点H作的垂线交于M,连接,若平分,问的度数是否为定值?若是,求出的度数;若不是,请说明理由.
【变式7-2】(2023下·山东济南·七年级统考期中)如图①,,点A,C分别在射线FE和FH上,.
(1)若,则的度数为______;
(2)小明同学发现,无论如何变化,的值始终为定值,并给出了一种证明该发现的辅助线作法:如图②,过点A作,交CD于点M.请你根据小明同学提供的辅助线,确定该定值,并说明理由;
(3)如图③,把“”改为“”,其他条件保持不变,猜想与的数量关系,并说明理由.
【变式7-3】(2023下·福建龙岩·七年级统考期末)如图1,点A、D分别在射线BM、CN线上,BM∥CN,BM⊥BC于点B,AE平分∠BAD交BC于点E,连接DE,∠1+∠2=90°.
(1)求证:AE⊥ED;
(2)求证:DE平分∠ADC;
(3)如图2,∠EAM和∠EDN的平分线交于点F,试猜想∠F的值是否为定值,若是,请予以证明;若不是,请说明理由.
【题型8 由平行线的判定与性质探究规律问题】
【例8】(2023下·四川成都·七年级树德中学校考阶段练习)(1)如图①,已知,图中,,之间有什么关系?
(2)如图②,已知,图中,,,之间有什么关系?
(3)如图③,已知,请直接写出图中,,,,之间的关系
(4)通过以上3个问题,你发现了什么规律?
【变式8-1】(2023上·广东江门·七年级江门市福泉奥林匹克学校校考阶段练习)如图,已知直线被直线所截,且,,分别平分,,,分别平分和,,分别平分,…依次规律,得点,则的度数为 .
【变式8-2】(2023下·河南郑州·七年级郑州外国语中学校考期中)在小学我们学过三角形的内角和等于;科学实验又证明,平面镜反射光线的规律是射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等.例如:在图①、图②中,都有,.设镜子与的夹角.
(1)如图①,若,,则_________;
(2)如图②,若,入射光线与反射光线的夹角.求的度数;
(3)如图③,若,设镜子与的夹角,入射光线与镜面的夹角,已知入射光线从镜面反射到镜面,再反射到镜面,最后经镜面反射后,当反射光线与入射光线平行时,探索与的数量关系,并说明理由.
【变式8-3】(2023上·广东广州·七年级广州市黄埔军校纪念中学校考开学考试)如图①所示,四边形为一张长方形纸片.如图②所示,将长方形纸片剪两刀,剪出三个角(、、),则 (度);
(1)如图③所示,将长方形纸片剪三刀,剪出四个角(、、、),则 (度);
(2)如图④所示,将长方形纸片剪四刀,剪出五个角(、、、、),则 (度);
(3)根据前面的探索规律,将本题按照上述剪法剪刀,剪出个角,那么这个角的和是 (度).
【题型9 由平行线的判定与性质解决三角尺问题】
【例9】(2023下·湖北孝感·七年级统考期末)将一副三角尺的直角顶点重合按如图放置,其中,,,.有下列结论:
(1)与互为补角;
(2)若,则;
(3)若,则;
(4)若,则.
其中正确的结论个数有( )
A.1个 B.2个 C.3个 D.4个
【变式9-1】(2023上·河南郑州·七年级校考期末)一副三角尺如图所示摆放,∠α 的大小为( )度
A.90 B.100 C.105 D.120
【变式9-2】(2023下·云南玉溪·七年级统考期末)含的三角板和含的三角板如图摆放,若,,,则的度数是( )
A. B. C. D.
【变式9-3】(2023下·贵州六盘水·七年级统考期末)如图,,将两块直角三角尺(一块含30°,一块含45°)按如下方式进行摆放,恰好满足,.
(1)求的度数;
(2)试判断与的位置关系,并说明理由.
【题型10 由平行线的判定与性质解决旋转问题】
【例10】(2023上·山西太原·七年级校考期末)问题情境:如图1,将含 角的三角板 和含角的三角板 叠放在一起,使直角顶点重合,点 D 落在直线 上,点 E 落在直线 上. 绕点 A 旋转, 边 与 、 分别相交与点 F、点N,边 与 相交于点 M.
(1)如图 2,当 时:
①求的度数.
②判断 与的数量关系,并说明理由.
(2)如图 3,当 平分 时:
①求的度数;
②判断 与 的位置关系,并说明理由.
【变式10-1】(2023下·重庆·七年级西南大学附中校考期中)如图,△OAB为等腰直角三角形(∠A=∠B=45°,∠AOB=90°),△OCD为等边三角形(∠C=∠D=∠COD=60°),满足OC>OA,△OCD绕点O从射线OC与射线OA重合的位置开始,逆时针旋转,旋转的角度为α(0°<α<360°),下列说法错误的是( )
A.当α=15°时,DC∥AB
B.当OC⊥AB时,α=45°
C.当边OB与边OD在同一直线上时,直线DC与直线AB相交形成的锐角为15°
D.整个旋转过程,共有10个位置使得△OAB与△OCD有一条边平行
【变式10-2】(2023下·四川成都·七年级校考期中)“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了A,D两座可旋转探照灯.假定主道路是平行的,即,,为上两点,平分交于点,为上一点,连接,平分交于点.
(1)若,则 ;
(2)作交于点,且满足,当时,试说明:;
(3)在(1)问的条件下,探照灯A、D照出的光线在铁路所在平面旋转,探照灯射出的光线以每秒5度的速度逆时针转动,探照灯射出的光线以每秒15度的速度逆时针转动,转至射线后立即以相同速度回转,若它们同时开始转动,设转动时间为秒,当回到出发时的位置时同时停止转动,则在转动过程中,当与互相平行或垂直时,请直接写出此时t的值.
【变式10-3】(2023下·湖北武汉·七年级统考期末)已知直线与直线、分别交于、两点,和的角平分线交于点,且.
(1)求证:;
(2)如图,和的角平分线交于点,求的度数;
(3)如图,若,延长线段得射线,延长线段得射线,射线绕点以每秒15°的速度逆时针旋转360°后停止,射线绕点以每秒3°的速度顺时针旋转180°以后停止.设它们同时旋转秒,问为多少时,射线,直接写出的值______秒.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
