3.1 用树状图或表格求概率 第2课时 课件(共16张PPT) 北师大版九年级上册数学
文档属性
| 名称 | 3.1 用树状图或表格求概率 第2课时 课件(共16张PPT) 北师大版九年级上册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 18:48:01 | ||
图片预览






文档简介
(共16张PPT)
第三章 概率的进一步认识
1 用树状图或表格求概率 第2课时
1.会借助树状图和列表法计算涉及两步或三步试验的随机事件发生的概率.
2.会借助概率判断游戏公平性问题.
◎重点:游戏的公平性.
故事导入
“抓阄抓出来的皇帝”这个故事大家听过吗?王莽末年,农民起义军四处寻找西汉刘氏皇室子弟当皇帝,以便以兴复汉室为借口来统领其他起义军.最终找到了西汉景王的后人刘盆子、刘茂和刘孝三人.只是这三人由谁来当皇帝,众起义军首领都争执不下.最后终于想了一法:抓阄.结果,刘盆子当了起义军的傀儡皇帝,一直当了三年.那这个游戏公平吗?
概率与游戏
阅读教材本课时相关内容,完成下列问题.
利用树状图或列表的方法表示游戏所有可能出现的结果时,应注意各种结果发生的可能性是 相同的 .
相同的
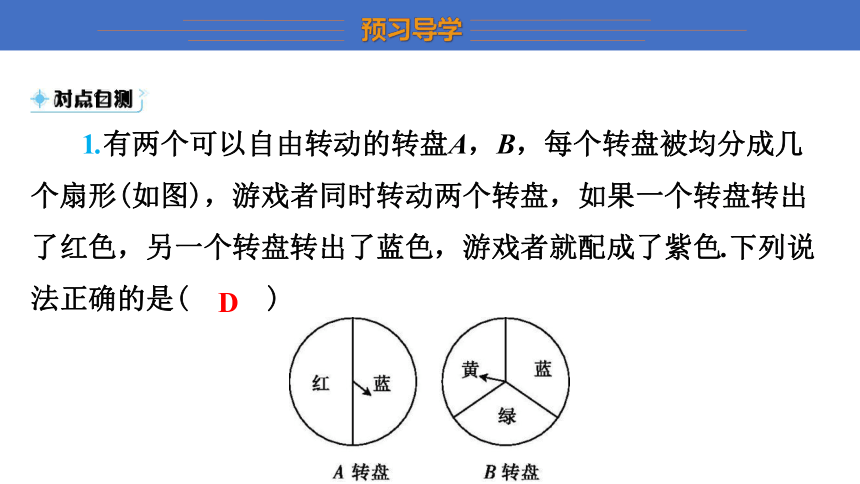
1.有两个可以自由转动的转盘A,B,每个转盘被均分成几个扇形(如图),游戏者同时转动两个转盘,如果一个转盘转出了红色,另一个转盘转出了蓝色,游戏者就配成了紫色.下列说法正确的是( D )
D
A.两个转盘转出蓝色的概率一样大
B.如果A转盘转出了蓝色,那么B转盘转出蓝色的可能性变小了
C.先转动A转盘再转动B转盘和同时转动两个转盘,游戏者配成紫色的概率不同
D.游戏者配成紫色的概率为
2.为积极响应“无偿献血,传递温暖”的号召,某高校一寝室的4名同学也用实际行动参与到爱心献血的活动中,他们其中有2个A型血,1个B型血,还有1个O型血.现从该寝室随机抽取两名同学参与第一批次献血,则抽取的两名同学都是A型血的概率为 .
5月19日为中国旅游日,衢州推出以“读万卷书,行万里路,游衢州景”为主题的旅游惠民活动,市民王先生准备在优惠日当天上午从孔氏南宗家庙、烂柯山、龙游石窟中随机选择一个地点,下午从江郎山、三衢石林、开化根博园中随机选择一个地点游玩,则王先生恰好上午选中孔氏南宗家庙,下午选中江郎山这两个地方的概率是( A )
A. B. C. D.
A
学生甲与学生乙玩一种转盘游戏.如图,这是两个完全相同的转盘,每个转盘被分成面积相等的四个区域,分别用数字“1”“2”“3”“4”表示.固定指针,同时转动两个转盘,任其自由停止,若两指针所指的数字之积为奇数,则甲获胜;若两指针所指的数字之积为偶数,则乙获胜;若出现指针指向扇形的分界线,则都重转一次.在该游戏中乙获胜的概率是 .
一个袋子中装有3个红球和2个黄球,这些球除颜色外其他完全相同,在看不到球的情况下,随机从袋子里同时摸出2个球,其中2个球的颜色相同的概率是 .
变式训练 四张小卡片上分别写有数字1、2、3、4.它们除数字外没有任何区别,将它们放在盒子里搅匀.
(1)随机地从盒子里抽取一张,求抽到数字2的概率.
(2)随机地从盒子里抽取一张.不放回再抽取第二张.请你用画树状图或列表的方法表示所有等可能的结果,并求抽到的数字之和为5的概率.
解:(1)P(抽到数字2)=.
(2)列举所有等可能的结果,画树状图如下:
共有12种等可能的结果,其中抽到的数字之和为5的占4种,
∴P(抽到的数字之和为5)==.
共有12种等可能的结果,其中抽到的数字之和为5的占4种,
∴P(抽到的数字之和为5)==.
甲、乙、丙三人之间相互传球,球从一个人手中随机传到另外一个人手中,共传球三次.若开始时球在甲手中,求经过三次传球后,球传回甲手中的概率是多少?
解:画树状图如图所示:三次传球有 8 种等可能的结果,其中传回甲手中的有 2 种,所以 P (传球三次回到甲手中)= =.
1.某一不透明袋子中装有红、绿小球各2个,除颜色外无其他差别.随机摸出一个小球后,不放回,再随机摸出一个,两次都摸到红球的概率为( B )
A. B. C. D.
B
2.学生甲与学生乙学习概率初步知识后设计了如下游戏:学生甲手中有6、8、9三张扑克牌,学生乙手中有5、7、10三张扑克牌,每人从各自手中取一张牌进行比较,数字大的本局获胜,每次取出的牌不能放回.
(1)若每人随机取出手中的一张牌进行比较,请列举出所有情况;
(2)求学生乙本局获胜的概率.
解:(1)画树状图如下:
由图可知,共有9种等可能的结果.
由图可知,共有9种等可能的结果.
(2)学生乙本局获胜的结果有4种,
所以学生乙本局获胜的概率为.
第三章 概率的进一步认识
1 用树状图或表格求概率 第2课时
1.会借助树状图和列表法计算涉及两步或三步试验的随机事件发生的概率.
2.会借助概率判断游戏公平性问题.
◎重点:游戏的公平性.
故事导入
“抓阄抓出来的皇帝”这个故事大家听过吗?王莽末年,农民起义军四处寻找西汉刘氏皇室子弟当皇帝,以便以兴复汉室为借口来统领其他起义军.最终找到了西汉景王的后人刘盆子、刘茂和刘孝三人.只是这三人由谁来当皇帝,众起义军首领都争执不下.最后终于想了一法:抓阄.结果,刘盆子当了起义军的傀儡皇帝,一直当了三年.那这个游戏公平吗?
概率与游戏
阅读教材本课时相关内容,完成下列问题.
利用树状图或列表的方法表示游戏所有可能出现的结果时,应注意各种结果发生的可能性是 相同的 .
相同的
1.有两个可以自由转动的转盘A,B,每个转盘被均分成几个扇形(如图),游戏者同时转动两个转盘,如果一个转盘转出了红色,另一个转盘转出了蓝色,游戏者就配成了紫色.下列说法正确的是( D )
D
A.两个转盘转出蓝色的概率一样大
B.如果A转盘转出了蓝色,那么B转盘转出蓝色的可能性变小了
C.先转动A转盘再转动B转盘和同时转动两个转盘,游戏者配成紫色的概率不同
D.游戏者配成紫色的概率为
2.为积极响应“无偿献血,传递温暖”的号召,某高校一寝室的4名同学也用实际行动参与到爱心献血的活动中,他们其中有2个A型血,1个B型血,还有1个O型血.现从该寝室随机抽取两名同学参与第一批次献血,则抽取的两名同学都是A型血的概率为 .
5月19日为中国旅游日,衢州推出以“读万卷书,行万里路,游衢州景”为主题的旅游惠民活动,市民王先生准备在优惠日当天上午从孔氏南宗家庙、烂柯山、龙游石窟中随机选择一个地点,下午从江郎山、三衢石林、开化根博园中随机选择一个地点游玩,则王先生恰好上午选中孔氏南宗家庙,下午选中江郎山这两个地方的概率是( A )
A. B. C. D.
A
学生甲与学生乙玩一种转盘游戏.如图,这是两个完全相同的转盘,每个转盘被分成面积相等的四个区域,分别用数字“1”“2”“3”“4”表示.固定指针,同时转动两个转盘,任其自由停止,若两指针所指的数字之积为奇数,则甲获胜;若两指针所指的数字之积为偶数,则乙获胜;若出现指针指向扇形的分界线,则都重转一次.在该游戏中乙获胜的概率是 .
一个袋子中装有3个红球和2个黄球,这些球除颜色外其他完全相同,在看不到球的情况下,随机从袋子里同时摸出2个球,其中2个球的颜色相同的概率是 .
变式训练 四张小卡片上分别写有数字1、2、3、4.它们除数字外没有任何区别,将它们放在盒子里搅匀.
(1)随机地从盒子里抽取一张,求抽到数字2的概率.
(2)随机地从盒子里抽取一张.不放回再抽取第二张.请你用画树状图或列表的方法表示所有等可能的结果,并求抽到的数字之和为5的概率.
解:(1)P(抽到数字2)=.
(2)列举所有等可能的结果,画树状图如下:
共有12种等可能的结果,其中抽到的数字之和为5的占4种,
∴P(抽到的数字之和为5)==.
共有12种等可能的结果,其中抽到的数字之和为5的占4种,
∴P(抽到的数字之和为5)==.
甲、乙、丙三人之间相互传球,球从一个人手中随机传到另外一个人手中,共传球三次.若开始时球在甲手中,求经过三次传球后,球传回甲手中的概率是多少?
解:画树状图如图所示:三次传球有 8 种等可能的结果,其中传回甲手中的有 2 种,所以 P (传球三次回到甲手中)= =.
1.某一不透明袋子中装有红、绿小球各2个,除颜色外无其他差别.随机摸出一个小球后,不放回,再随机摸出一个,两次都摸到红球的概率为( B )
A. B. C. D.
B
2.学生甲与学生乙学习概率初步知识后设计了如下游戏:学生甲手中有6、8、9三张扑克牌,学生乙手中有5、7、10三张扑克牌,每人从各自手中取一张牌进行比较,数字大的本局获胜,每次取出的牌不能放回.
(1)若每人随机取出手中的一张牌进行比较,请列举出所有情况;
(2)求学生乙本局获胜的概率.
解:(1)画树状图如下:
由图可知,共有9种等可能的结果.
由图可知,共有9种等可能的结果.
(2)学生乙本局获胜的结果有4种,
所以学生乙本局获胜的概率为.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
