4.3.1中心对称教学课件(共31张PPT) 鲁教版(五四制)八年级数学上册
文档属性
| 名称 | 4.3.1中心对称教学课件(共31张PPT) 鲁教版(五四制)八年级数学上册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 889.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-16 00:00:00 | ||
图片预览



文档简介
(共31张PPT)
4.3-1 中心对称
1.了解两图形成中心对称的定义,掌握成中心对称的性质 。
2.会画一个图形关于某一点成中心对称的图形。
学习目标
低阶目标
高阶目标
经历有关成中心对称的观察、操作的过程,增强动手实践能力。
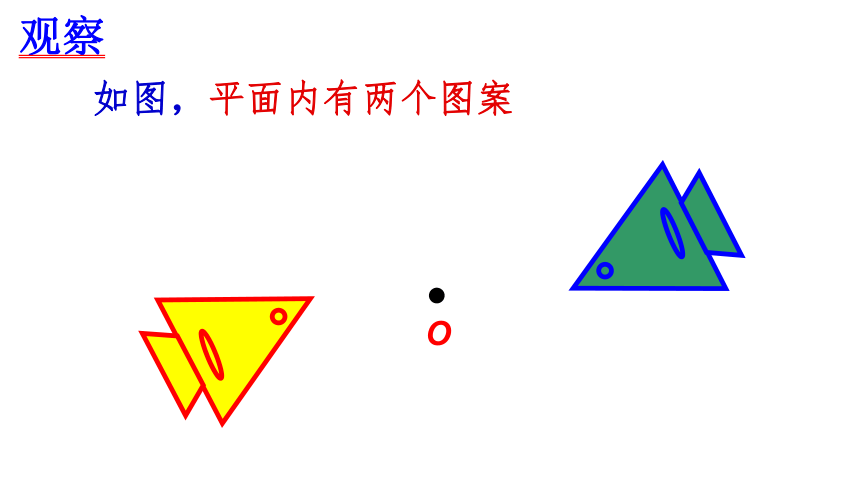
如图,平面内有两个图案
观察
O
O
180°
绕点O旋转了180度后,一个图案和另一个重合。
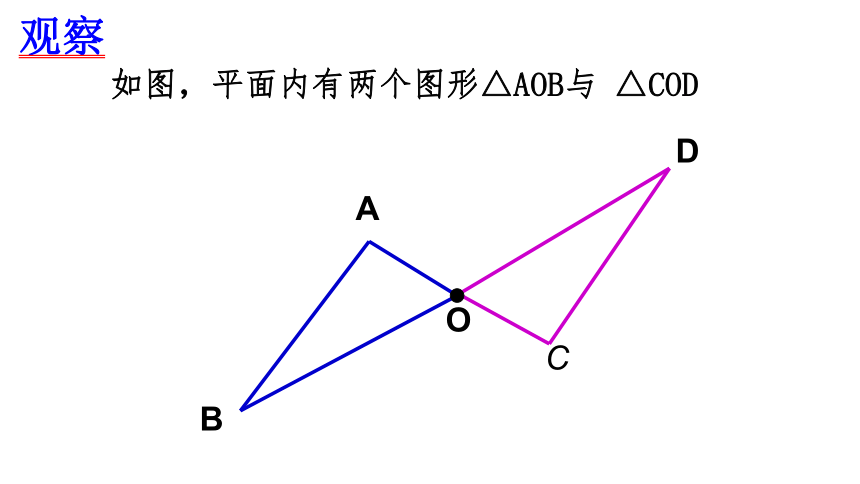
观察
如图,平面内有两个图形△AOB与 △COD
A
B
C
D
O
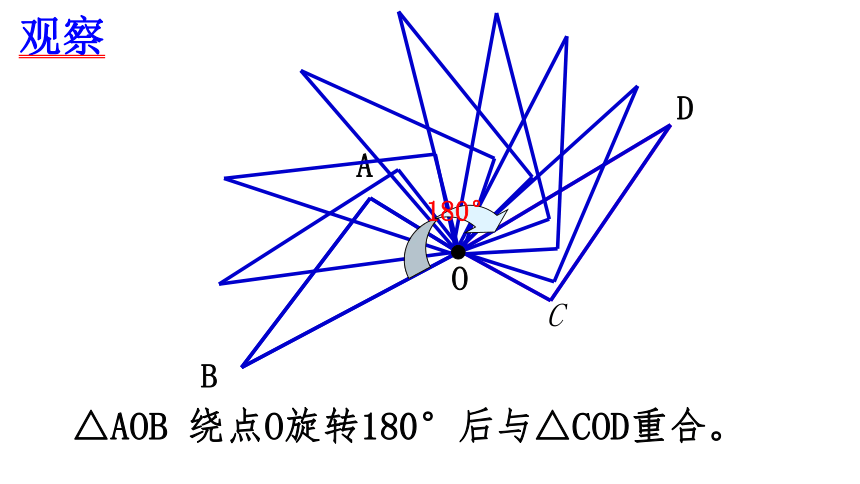
观察
A
B
C
D
O
180°
△AOB 绕点O旋转180°后与△COD重合。
观察
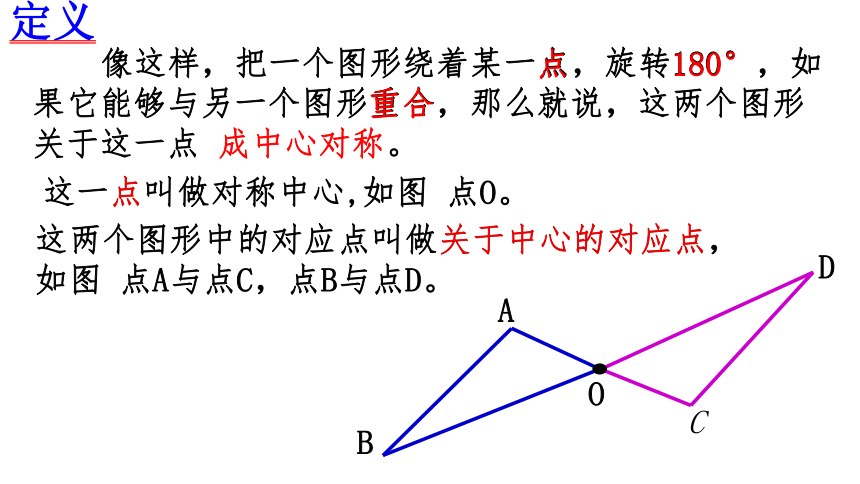
像这样,把一个图形绕着某一点,旋转180°,如果它能够与另一个图形重合,那么就说,这两个图形 关于这一点 成中心对称。
这一点叫做对称中心,如图 点O。
这两个图形中的对应点叫做关于中心的对应点,如图 点A与点C,点B与点D。
定义
A
B
C
D
O
点
180°
重合
O
A
B
C
D
E
F
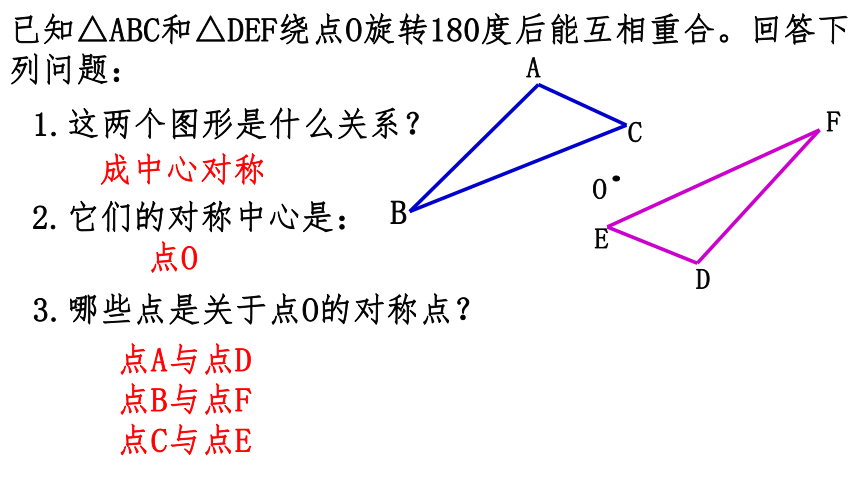
已知△ABC和△DEF绕点O旋转180度后能互相重合。回答下列问题:
1.这两个图形是什么关系?
成中心对称
2.它们的对称中心是:
点O
3.哪些点是关于点O的对称点?
点A与点D
点B与点F
点C与点E
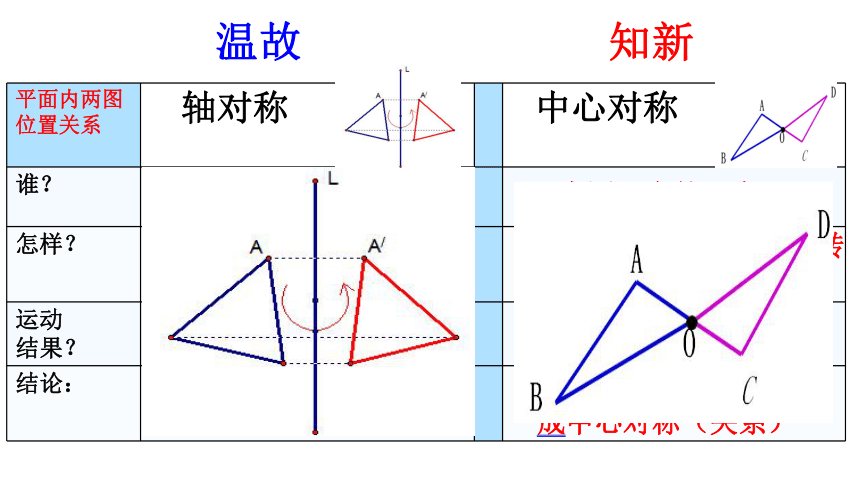
平面内两图位置关系
轴对称 中心对称
谁? 两个图形中的一个
怎样?
沿一直线(对称轴)
翻折180度
运动
结果? 与另一个重合
结论: 这两个图形关于这直线成轴对称(关系)
两个图形中的一个
与另一个重合
对称中心
这两个图形关于这点成中心对称(关系)
绕一点( )旋转180度
温故
知新
A
B
C
A’
C’
B’
O
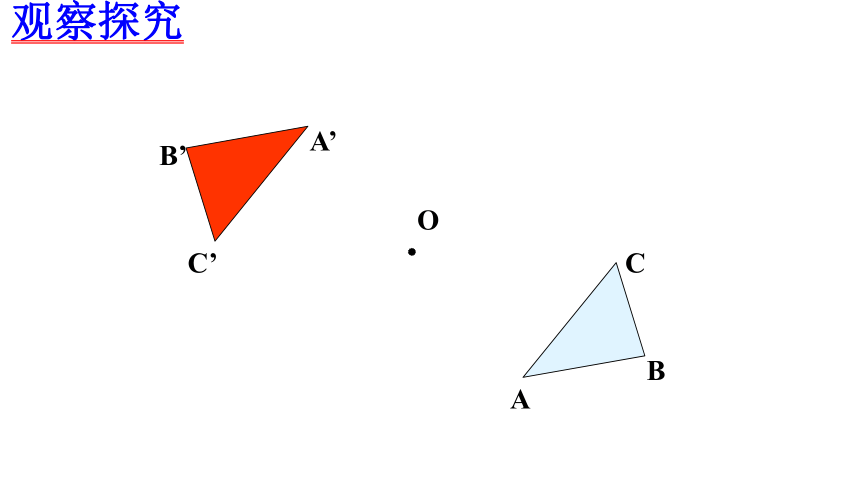
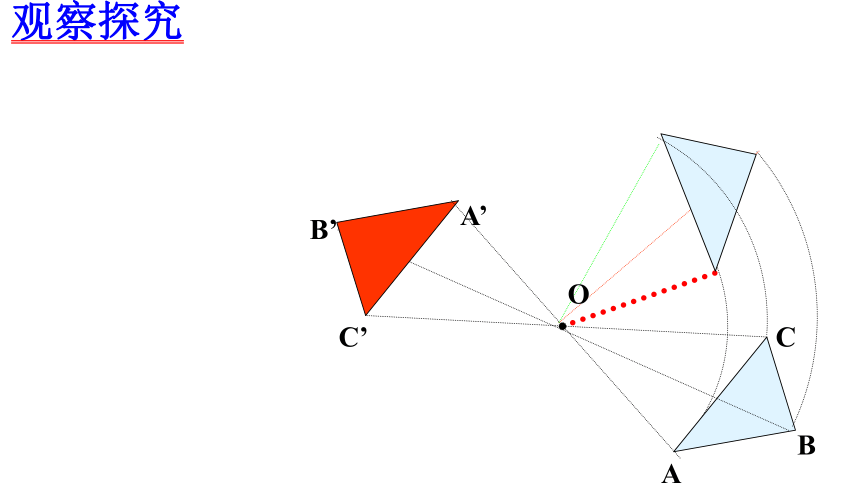
观察探究
A
B
C
A’
C’
B’
O
观察探究
A
B
C
A’
C’
B’
O
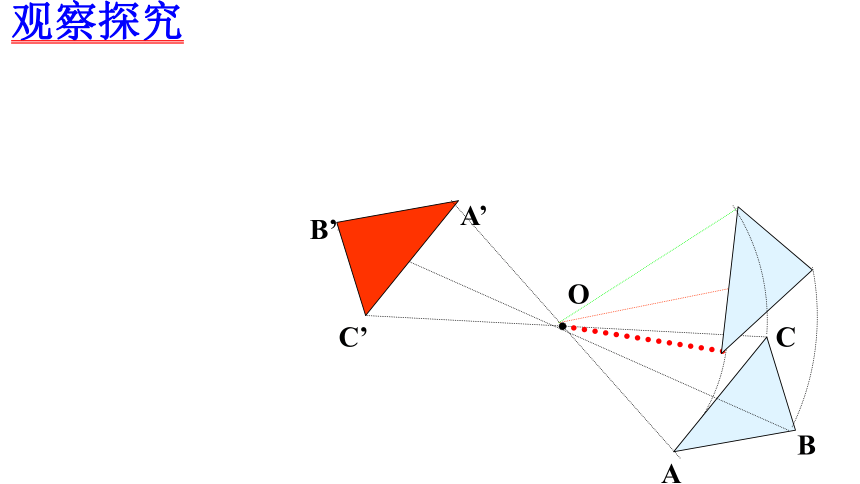
观察探究
A
B
C
A’
C’
B’
O
观察探究
A
B
C
A’
C’
B’
O
观察探究
A
B
C
A’
C’
B’
O
观察探究
A
B
C
A’
C’
B’
O
观察探究
2.成中心对称
1.旋转180°
3.半径OA=OA'
OB=OB′
OC=OC′
4.重合,即:△ABC≌△A′B′C′
问题
B'
C'
A'
A
B
C
O
1、A、O、A'三点共线时,A点旋转了多少度?
2、平面内这两个图形成什么位置关系?
3、A、B、C各自旋转半径是什么?
4、两图形运动结果如何?
探究归纳
2、A点绕O,旋转-180度-平角,到A'说明:AOA'三点( ),对称点A与A'的连线段AA'过( ),即:( )
3、旋转半径OA=OA'说明:线段AA'被点O( )即:( )
4、两图形重合说明:( )
1、(绕点O--旋转180度---重合)说明:这两个图形( )
B'
C'
A'
B
C
O
A
成中心对称
共线
对称点的连线段被对称中心平分
点O
对称点的连线过对称中心
两图形全等
2、A点绕O,旋转-180度-平角,到A'说明:AOA'三点( ),对称点A与A'的连线段AA'过( ),即:( )
3、旋转半径OA=OA'说明:线段AA'被点O( )即:( )
4、两图形重合说明:( )
1、(绕点O--旋转180度---重合)说明:这两个图形( )
平分
探究归纳
B'
C'
A'
B
C
O
A
(1)关于中心对称的两个图形,
(2)关于中心对称的两个图形
对应点的连线经过对称中心,且被对称中心平分
全等
成中心对称的性质
探究归纳
如图,选择点O为对称中心,画出点A关于点O的对称点A'.
A
O
画法:1.连接AO并延长。
2.在AO的延长线上
截取OA' =OA。
点A'即为所求。
A’
根据性质:∵点A与点A'关于O中心对称
∴O A’ =OA(被平分)
归纳应用
已知线段AB和O点,画出线段AB关于点O的对称线段A' B'
O
A'
B'
A
B
连结AO并延长到A' ,使OA' =OA,则得A的对称点A'
连结BO并延长到B',使OB'=OB,则得B的对称点B'
连结A'B',则线段A'B'是所画线段
归纳应用
如图,选择点O为对称中心,画出与△ABC关于点O对称的△A' B' C'.
O
C
B
A
C’
A’
B’
归纳应用
△A' B' C'即为所求。
如图,选择点O为对称中心,画出与△ ABC关于点O对称的△A' B' C'.
O
C
B
A
C’
A’
B’
归纳应用
画一个图形关于某点的对称图形的画法是:
(1)画一个点关于某点(对称中心)的对称点的画法是先连接这个点与对称中心并延长一倍即可。
(2)画一个图形关于某点的对称图形的画法是先画出图形中的几个关键点关于某点的对称点,然后再顺次连结有关对称点即可。
方法总结
课堂小结
1.了解两图形成中心对称的定义,掌握中心对称的性质 。
2.会画一个图形关于某一点成中心对称的图形。
学习目标
1个定义
2条性质
1种画法
1. 判断正误:
(1)轴对称的两个图形一定是全等形,但全等的两个图形不一定是轴对称的图形.( )
(2)成中心对称的两个图形一定是全等形,但全等的两个图形不一定是成中心对称的图形. ( )
(3)全等的两个图形,不是成中心对称的图形,就是成轴对称的图形. ( )
√
√
×
当堂检测
2. 下列五组图形中,左边的图形与右边的图形成中心对称的有( )
A.1 组 B.2 组 C.3 组 D.4 组
B
当堂检测
3. 如图,已知△AOB 与△DOC 成中心对称,△AOB 的周长是 8,AB=3,则 OC + OD=( )
A. 3 B. 5
C. 6 D. 8
A
B
C
D
O
B
当堂检测
4. 如图,△ABO与△CDO关于O点中心对称,点E、F在线段AC上,且AF =CE.
求证:DF =BE.
作业设置
1.必做题:导学案巩固训练 1、2、3、4题
2.选做题:导学案——能力提升题
思考:
怎样判别两个图形关于某一点成中心对称呢?
4.3-1 中心对称
1.了解两图形成中心对称的定义,掌握成中心对称的性质 。
2.会画一个图形关于某一点成中心对称的图形。
学习目标
低阶目标
高阶目标
经历有关成中心对称的观察、操作的过程,增强动手实践能力。
如图,平面内有两个图案
观察
O
O
180°
绕点O旋转了180度后,一个图案和另一个重合。
观察
如图,平面内有两个图形△AOB与 △COD
A
B
C
D
O
观察
A
B
C
D
O
180°
△AOB 绕点O旋转180°后与△COD重合。
观察
像这样,把一个图形绕着某一点,旋转180°,如果它能够与另一个图形重合,那么就说,这两个图形 关于这一点 成中心对称。
这一点叫做对称中心,如图 点O。
这两个图形中的对应点叫做关于中心的对应点,如图 点A与点C,点B与点D。
定义
A
B
C
D
O
点
180°
重合
O
A
B
C
D
E
F
已知△ABC和△DEF绕点O旋转180度后能互相重合。回答下列问题:
1.这两个图形是什么关系?
成中心对称
2.它们的对称中心是:
点O
3.哪些点是关于点O的对称点?
点A与点D
点B与点F
点C与点E
平面内两图位置关系
轴对称 中心对称
谁? 两个图形中的一个
怎样?
沿一直线(对称轴)
翻折180度
运动
结果? 与另一个重合
结论: 这两个图形关于这直线成轴对称(关系)
两个图形中的一个
与另一个重合
对称中心
这两个图形关于这点成中心对称(关系)
绕一点( )旋转180度
温故
知新
A
B
C
A’
C’
B’
O
观察探究
A
B
C
A’
C’
B’
O
观察探究
A
B
C
A’
C’
B’
O
观察探究
A
B
C
A’
C’
B’
O
观察探究
A
B
C
A’
C’
B’
O
观察探究
A
B
C
A’
C’
B’
O
观察探究
A
B
C
A’
C’
B’
O
观察探究
2.成中心对称
1.旋转180°
3.半径OA=OA'
OB=OB′
OC=OC′
4.重合,即:△ABC≌△A′B′C′
问题
B'
C'
A'
A
B
C
O
1、A、O、A'三点共线时,A点旋转了多少度?
2、平面内这两个图形成什么位置关系?
3、A、B、C各自旋转半径是什么?
4、两图形运动结果如何?
探究归纳
2、A点绕O,旋转-180度-平角,到A'说明:AOA'三点( ),对称点A与A'的连线段AA'过( ),即:( )
3、旋转半径OA=OA'说明:线段AA'被点O( )即:( )
4、两图形重合说明:( )
1、(绕点O--旋转180度---重合)说明:这两个图形( )
B'
C'
A'
B
C
O
A
成中心对称
共线
对称点的连线段被对称中心平分
点O
对称点的连线过对称中心
两图形全等
2、A点绕O,旋转-180度-平角,到A'说明:AOA'三点( ),对称点A与A'的连线段AA'过( ),即:( )
3、旋转半径OA=OA'说明:线段AA'被点O( )即:( )
4、两图形重合说明:( )
1、(绕点O--旋转180度---重合)说明:这两个图形( )
平分
探究归纳
B'
C'
A'
B
C
O
A
(1)关于中心对称的两个图形,
(2)关于中心对称的两个图形
对应点的连线经过对称中心,且被对称中心平分
全等
成中心对称的性质
探究归纳
如图,选择点O为对称中心,画出点A关于点O的对称点A'.
A
O
画法:1.连接AO并延长。
2.在AO的延长线上
截取OA' =OA。
点A'即为所求。
A’
根据性质:∵点A与点A'关于O中心对称
∴O A’ =OA(被平分)
归纳应用
已知线段AB和O点,画出线段AB关于点O的对称线段A' B'
O
A'
B'
A
B
连结AO并延长到A' ,使OA' =OA,则得A的对称点A'
连结BO并延长到B',使OB'=OB,则得B的对称点B'
连结A'B',则线段A'B'是所画线段
归纳应用
如图,选择点O为对称中心,画出与△ABC关于点O对称的△A' B' C'.
O
C
B
A
C’
A’
B’
归纳应用
△A' B' C'即为所求。
如图,选择点O为对称中心,画出与△ ABC关于点O对称的△A' B' C'.
O
C
B
A
C’
A’
B’
归纳应用
画一个图形关于某点的对称图形的画法是:
(1)画一个点关于某点(对称中心)的对称点的画法是先连接这个点与对称中心并延长一倍即可。
(2)画一个图形关于某点的对称图形的画法是先画出图形中的几个关键点关于某点的对称点,然后再顺次连结有关对称点即可。
方法总结
课堂小结
1.了解两图形成中心对称的定义,掌握中心对称的性质 。
2.会画一个图形关于某一点成中心对称的图形。
学习目标
1个定义
2条性质
1种画法
1. 判断正误:
(1)轴对称的两个图形一定是全等形,但全等的两个图形不一定是轴对称的图形.( )
(2)成中心对称的两个图形一定是全等形,但全等的两个图形不一定是成中心对称的图形. ( )
(3)全等的两个图形,不是成中心对称的图形,就是成轴对称的图形. ( )
√
√
×
当堂检测
2. 下列五组图形中,左边的图形与右边的图形成中心对称的有( )
A.1 组 B.2 组 C.3 组 D.4 组
B
当堂检测
3. 如图,已知△AOB 与△DOC 成中心对称,△AOB 的周长是 8,AB=3,则 OC + OD=( )
A. 3 B. 5
C. 6 D. 8
A
B
C
D
O
B
当堂检测
4. 如图,△ABO与△CDO关于O点中心对称,点E、F在线段AC上,且AF =CE.
求证:DF =BE.
作业设置
1.必做题:导学案巩固训练 1、2、3、4题
2.选做题:导学案——能力提升题
思考:
怎样判别两个图形关于某一点成中心对称呢?
