5.9弧长及扇形的面积 课件 (共20张PPT)鲁教版(五四制)数学九年级下册
文档属性
| 名称 | 5.9弧长及扇形的面积 课件 (共20张PPT)鲁教版(五四制)数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1020.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 12:49:15 | ||
图片预览








文档简介
(共20张PPT)
5.9弧长及扇形的面积
学习目标
1.掌握弧长和扇形面积的计算公式,并会应用公式解决问题。
2.会计算弓形的面积,体会类比和转化思想
如图,某传送带的一个转动轮的半径为10cm.
1.转动轮转一周,传送带上的物品A被传送多少厘米
2.转动轮转1°,传送带上的物品A被传送多少厘米
3.转动轮转n°,传送带上的物品A被传送多少厘米
一、情境导入
二、探索新知
活动一:探究弧长公式
no
R
O
l
(1)圆的周长是多少?
(2)圆的周长可以看作多少度的圆心角所对的弧长?
如右图所示,圆的半径为R
(3)1°圆心角所对弧长与圆的周长有何关系?
(4)50°的圆心角所对弧长是多少?
(5)n°的圆心角所对弧长是多少?
R
活动一:探究弧长计算公式
思考:弧长与哪些因素有关:
(1)与圆心角大小(n)有关
(2)与半径长短(R)有关
注意:
公式中n表示1°的圆心角的倍数,计算时n不带单位。
归纳:在半径为R的圆中,n°的圆心角所对弧长 l ,计算公式为:
二、探索新知
如图,某传送带的一个转动轮的半径为10cm.
1.转动轮转一周,传送带上的物品A被传送多少厘米
2.转动轮转1°,传送带上的物品A被传送多少厘米
3.转动轮转n°,传送带上的物品A被传送多少厘米
二、巩固练习
活动一:探索弧长公式
解决问题:
制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图中所示管道的展直长度 l (结果保留,单位:mm)
例1:
思考:
展直长度指的是谁的长?
例题解析
活动一:探索弧长公式
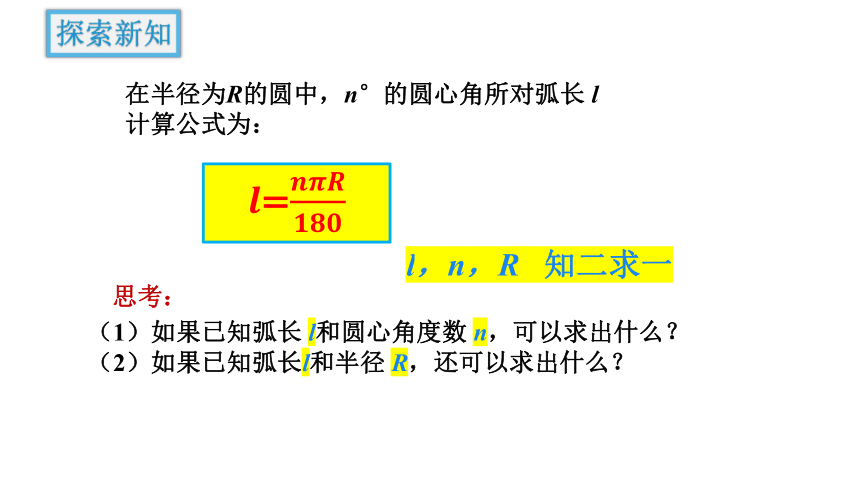
在半径为R的圆中,n°的圆心角所对弧长 l
计算公式为:
l,n,R 知二求一
探索新知
(1)如果已知弧长 l和圆心角度数 n,可以求出什么?
(2)如果已知弧长l和半径 R,还可以求出什么?
思考:
=
巩固练习
1.一个扇形半径是3,圆心角是240°,这个扇形的弧长是( )
A. 2π B. π C. 4π D. 12π
2.已知圆的一段弧长为4π cm,它所对的圆心角为100°,
该圆的半径为 .
练习1
C
O
扇形
由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形。
扇形的定义
O
B
A
扇形
探索新知
(2)圆心角为1°的扇形面积是多少?
(3)圆心角为n°的扇形面积是多少?
结 论 :如果用字母 S 表示扇形的面积,n表示圆心角的度数,R 表示圆半径,那么扇形面积的计算公式是:
探索新知
活动二:探究扇形面积公式
(1)圆的面积是多少?
已知圆的半径为R
探求新知
R
n°
l
思考
观察比较两个公式
扇形面积 S 与弧长 l 之间是否存在某种等量关系呢?
=
=
=
活动三:探究弧长和扇形面积公式之间的关系
试一试
9πm2
。
。
n
例题解析
例2 扇形AOB的半径为12cm,∠AOB=120°,求AB的长和扇形AOB的面积(结果保留).
1. 已知扇形的圆心角为120°,半径为20,则该扇形的面积____.
2.已知扇形面积为 ,圆心角为60°,则这个扇形的半径R=___.
3. 已知半径为2cm的扇形,其弧长为,则这个扇形的面积是_________.
对应练习
如图是水平放置的一个油管,横截面半径为12cm,其中,有油的部分油高是6cm,求截面上有油部分的面积.(结果保留)
拓展提高——求不规则图形的面积(弓形)
②当弓形面积大于半圆时
S弓形= S扇形+S△
①当弓形面积小于半圆时
S弓形= S扇形-S△
A
B
拓展提高——求不规则图形的面积(弓形)
转化思想
类比思想
如果扇形的半径为r,圆心角为n°,那么
课堂小结
①当弓形面积小于半圆时
S弓形= S扇形-S△
②当弓形面积大于半圆时
S弓形= S扇形+S△
弧长和扇形的面积公式
弓形的面积
转化思想
=
=
=
类比思想
从特殊到一般
当堂检测
1、半径为6,圆心角为1200的扇形的面积是( )
A、3 B、6 C、9 D、12
2、已知扇形的圆心角为120°,面积是3cm2,那么这个扇形的半径是( )A、1cm B、3cm C、 6cm D、9cm
3、如图,从一块直径为2m的圆形铁皮上剪出一个圆心角为900
的扇形,则此扇形的面积为( )
4、数学课上,老师将如图所示的边长为1的正方形铁丝框变形成以
点A为圆心,AB为半径的扇形,则所得扇形DAB的面积
下课
5.9弧长及扇形的面积
学习目标
1.掌握弧长和扇形面积的计算公式,并会应用公式解决问题。
2.会计算弓形的面积,体会类比和转化思想
如图,某传送带的一个转动轮的半径为10cm.
1.转动轮转一周,传送带上的物品A被传送多少厘米
2.转动轮转1°,传送带上的物品A被传送多少厘米
3.转动轮转n°,传送带上的物品A被传送多少厘米
一、情境导入
二、探索新知
活动一:探究弧长公式
no
R
O
l
(1)圆的周长是多少?
(2)圆的周长可以看作多少度的圆心角所对的弧长?
如右图所示,圆的半径为R
(3)1°圆心角所对弧长与圆的周长有何关系?
(4)50°的圆心角所对弧长是多少?
(5)n°的圆心角所对弧长是多少?
R
活动一:探究弧长计算公式
思考:弧长与哪些因素有关:
(1)与圆心角大小(n)有关
(2)与半径长短(R)有关
注意:
公式中n表示1°的圆心角的倍数,计算时n不带单位。
归纳:在半径为R的圆中,n°的圆心角所对弧长 l ,计算公式为:
二、探索新知
如图,某传送带的一个转动轮的半径为10cm.
1.转动轮转一周,传送带上的物品A被传送多少厘米
2.转动轮转1°,传送带上的物品A被传送多少厘米
3.转动轮转n°,传送带上的物品A被传送多少厘米
二、巩固练习
活动一:探索弧长公式
解决问题:
制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图中所示管道的展直长度 l (结果保留,单位:mm)
例1:
思考:
展直长度指的是谁的长?
例题解析
活动一:探索弧长公式
在半径为R的圆中,n°的圆心角所对弧长 l
计算公式为:
l,n,R 知二求一
探索新知
(1)如果已知弧长 l和圆心角度数 n,可以求出什么?
(2)如果已知弧长l和半径 R,还可以求出什么?
思考:
=
巩固练习
1.一个扇形半径是3,圆心角是240°,这个扇形的弧长是( )
A. 2π B. π C. 4π D. 12π
2.已知圆的一段弧长为4π cm,它所对的圆心角为100°,
该圆的半径为 .
练习1
C
O
扇形
由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形。
扇形的定义
O
B
A
扇形
探索新知
(2)圆心角为1°的扇形面积是多少?
(3)圆心角为n°的扇形面积是多少?
结 论 :如果用字母 S 表示扇形的面积,n表示圆心角的度数,R 表示圆半径,那么扇形面积的计算公式是:
探索新知
活动二:探究扇形面积公式
(1)圆的面积是多少?
已知圆的半径为R
探求新知
R
n°
l
思考
观察比较两个公式
扇形面积 S 与弧长 l 之间是否存在某种等量关系呢?
=
=
=
活动三:探究弧长和扇形面积公式之间的关系
试一试
9πm2
。
。
n
例题解析
例2 扇形AOB的半径为12cm,∠AOB=120°,求AB的长和扇形AOB的面积(结果保留).
1. 已知扇形的圆心角为120°,半径为20,则该扇形的面积____.
2.已知扇形面积为 ,圆心角为60°,则这个扇形的半径R=___.
3. 已知半径为2cm的扇形,其弧长为,则这个扇形的面积是_________.
对应练习
如图是水平放置的一个油管,横截面半径为12cm,其中,有油的部分油高是6cm,求截面上有油部分的面积.(结果保留)
拓展提高——求不规则图形的面积(弓形)
②当弓形面积大于半圆时
S弓形= S扇形+S△
①当弓形面积小于半圆时
S弓形= S扇形-S△
A
B
拓展提高——求不规则图形的面积(弓形)
转化思想
类比思想
如果扇形的半径为r,圆心角为n°,那么
课堂小结
①当弓形面积小于半圆时
S弓形= S扇形-S△
②当弓形面积大于半圆时
S弓形= S扇形+S△
弧长和扇形的面积公式
弓形的面积
转化思想
=
=
=
类比思想
从特殊到一般
当堂检测
1、半径为6,圆心角为1200的扇形的面积是( )
A、3 B、6 C、9 D、12
2、已知扇形的圆心角为120°,面积是3cm2,那么这个扇形的半径是( )A、1cm B、3cm C、 6cm D、9cm
3、如图,从一块直径为2m的圆形铁皮上剪出一个圆心角为900
的扇形,则此扇形的面积为( )
4、数学课上,老师将如图所示的边长为1的正方形铁丝框变形成以
点A为圆心,AB为半径的扇形,则所得扇形DAB的面积
下课
