11.1.3三角形的稳定性 课件(共20张PPT) 人教版数学八年级上册
文档属性
| 名称 | 11.1.3三角形的稳定性 课件(共20张PPT) 人教版数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-16 00:37:31 | ||
图片预览




文档简介
(共20张PPT)
11.1.3三角形的稳定性
2023—2024学年人教版数学八年级上册
1.三角形的高:
从△ABC 的顶点 A 向它所对的边 BC 所在直线画_____,____为 D,所得线段 AD 叫做△ABC 的边 BC 上的高.
(1)锐角三角形的三条高都在三角形的内部,且交于三角形_______.
(2)直角三角形的三条高交于_________.
(3)钝角三角形的三条高所在的直线交于三角形_______.
垂线
垂足
内一点
直角顶点
外一点
连接△ABC 的_____A 和它所对的边 BC 的_____D,所得线段 AD 叫做△ABC 的边 BC 上的中线.
三角形的三条中线___________.
三角形三条中线的交点叫做三角形的_____.
3.三角形的角平分线:
画∠A 的_______AD,交∠A 所对的边 BC 于点 D,所得线段 AD 叫做△ABC 的角平分线.
2.三角形的中线:
顶点
中点
相交于一点
重心
平分线
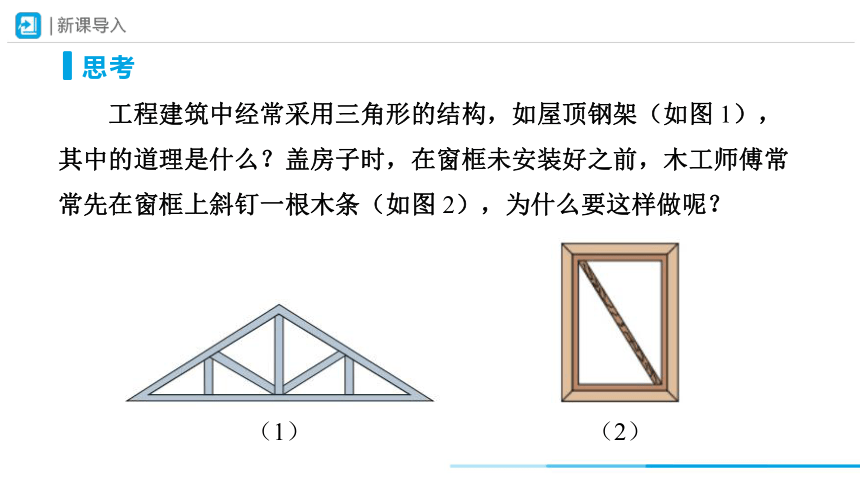
工程建筑中经常采用三角形的结构,如屋顶钢架(如图 1),其中的道理是什么?盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条(如图 2),为什么要这样做呢?
思考
(1)
(2)
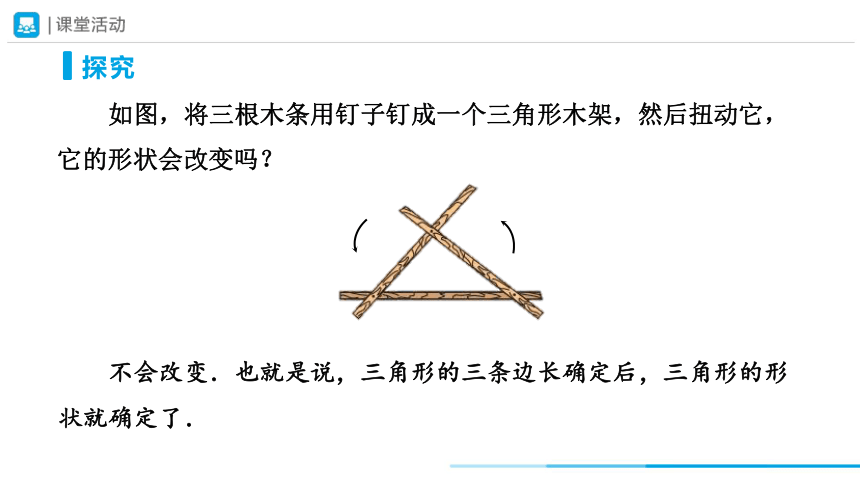
如图,将三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?
探究
不会改变.也就是说,三角形的三条边长确定后,三角形的形状就确定了.
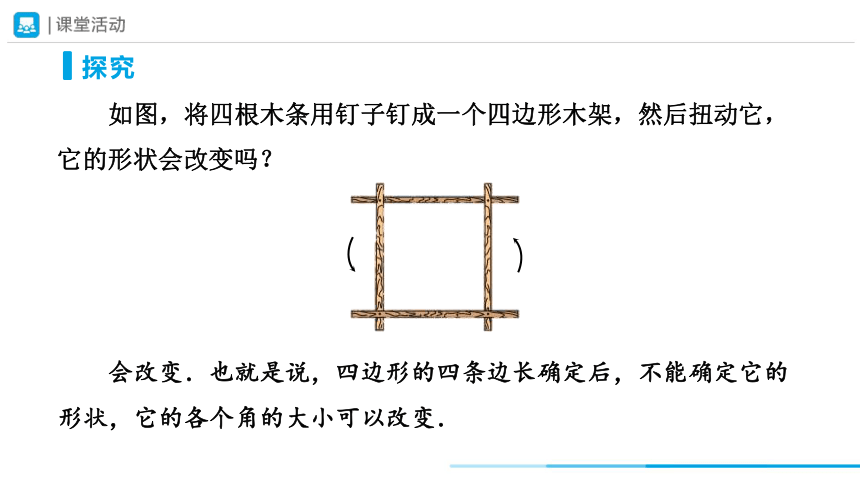
如图,将四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?
探究
会改变.也就是说,四边形的四条边长确定后,不能确定它的形状,它的各个角的大小可以改变.
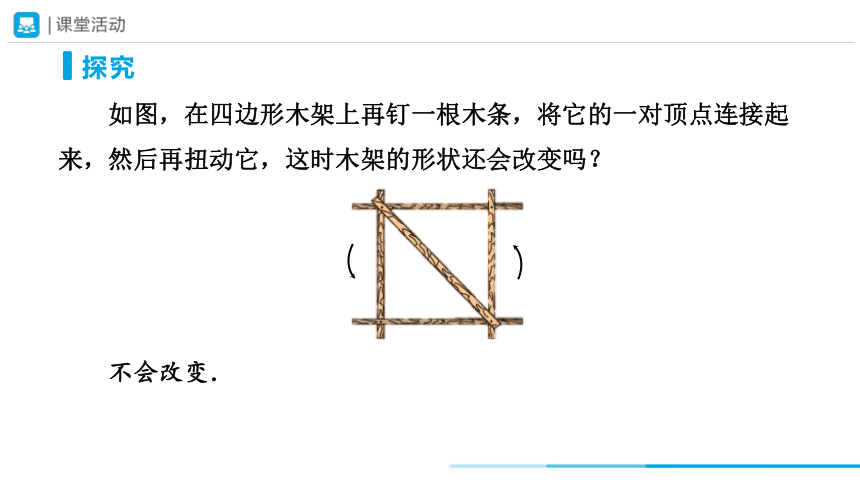
如图,在四边形木架上再钉一根木条,将它的一对顶点连接起来,然后再扭动它,这时木架的形状还会改变吗?
探究
不会改变.
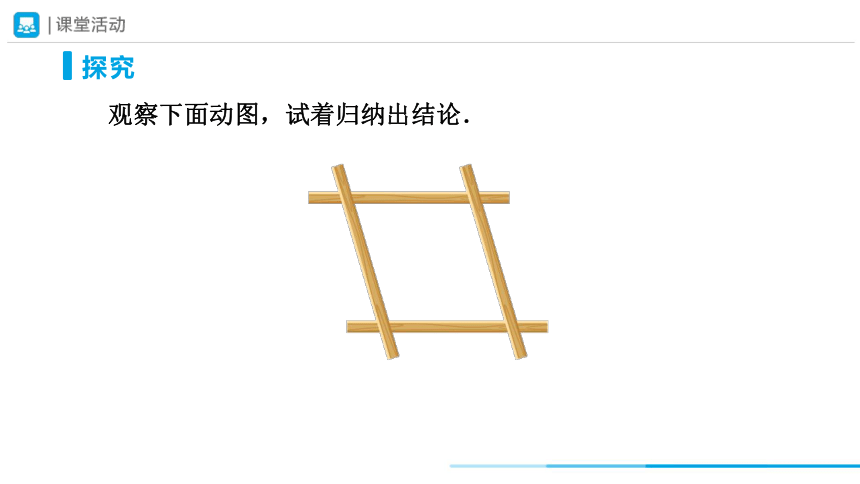
观察下面动图,试着归纳出结论.
探究
观察下面动图,试着归纳出结论.
探究
可以发现,三角形木架的形状不会改变,而四边形木架的形状会改变.这就是说,三角形是具有稳定性的图形,而四边形没有稳定性.
还可以发现,斜钉一根木条的四边形木架的形状不会改变.这是因为斜钉一根木条后,四边形变成两个三角形,由于三角形有稳定性,斜钉一根木条的窗框在未安装好之前也不会变形.
归纳
三角形的稳定性有广泛的应用,你能举出一些例子吗?
问题
钢架桥
起重机
三角形的稳定性有广泛的应用,你能举出一些例子吗?
问题
国家体育场
输电铁塔
四边形的不稳定性也有广泛的应用,你能举出一些例子吗?
问题
活动挂架
伸缩门
例 1 以下不是利用三角形稳定性的是( ).
A.在门框上斜钉一根木条
B.高架桥的三角形结构
C.伸缩衣挂
D.屋顶的三角形钢架
解析:伸缩衣挂是四边形结构,利用的是四边形的不稳定性.
C
归纳
三角形的稳定性——小性质,大用途
三角形的稳定性的实质是三角形的各边的长度被确定后,其形状不会再发生改变.现实生活中常常利用这一性质,将原本不稳定的形状转化为三角形,使之稳定.
例 2 观察下列图形,回答问题.
(1)图形中具有稳定性的是_______(只填序号);
①
②
③
④
⑤
①④⑤
例 2 观察下列图形,回答问题.
(2)对不具有稳定性的图形,请适当地添加线段,使之具有稳定性.
①
②
③
④
⑤
答案不唯一.
对于比较复杂的图形,只要使整个图形均由三角形构成,就能使整个图形具有稳定性.
归纳
三角形的稳定性
四边形
三角形
稳定性
不稳定性
三角形的稳定性与四边形的不稳定性的应用
谢谢
11.1.3三角形的稳定性
2023—2024学年人教版数学八年级上册
1.三角形的高:
从△ABC 的顶点 A 向它所对的边 BC 所在直线画_____,____为 D,所得线段 AD 叫做△ABC 的边 BC 上的高.
(1)锐角三角形的三条高都在三角形的内部,且交于三角形_______.
(2)直角三角形的三条高交于_________.
(3)钝角三角形的三条高所在的直线交于三角形_______.
垂线
垂足
内一点
直角顶点
外一点
连接△ABC 的_____A 和它所对的边 BC 的_____D,所得线段 AD 叫做△ABC 的边 BC 上的中线.
三角形的三条中线___________.
三角形三条中线的交点叫做三角形的_____.
3.三角形的角平分线:
画∠A 的_______AD,交∠A 所对的边 BC 于点 D,所得线段 AD 叫做△ABC 的角平分线.
2.三角形的中线:
顶点
中点
相交于一点
重心
平分线
工程建筑中经常采用三角形的结构,如屋顶钢架(如图 1),其中的道理是什么?盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条(如图 2),为什么要这样做呢?
思考
(1)
(2)
如图,将三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?
探究
不会改变.也就是说,三角形的三条边长确定后,三角形的形状就确定了.
如图,将四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?
探究
会改变.也就是说,四边形的四条边长确定后,不能确定它的形状,它的各个角的大小可以改变.
如图,在四边形木架上再钉一根木条,将它的一对顶点连接起来,然后再扭动它,这时木架的形状还会改变吗?
探究
不会改变.
观察下面动图,试着归纳出结论.
探究
观察下面动图,试着归纳出结论.
探究
可以发现,三角形木架的形状不会改变,而四边形木架的形状会改变.这就是说,三角形是具有稳定性的图形,而四边形没有稳定性.
还可以发现,斜钉一根木条的四边形木架的形状不会改变.这是因为斜钉一根木条后,四边形变成两个三角形,由于三角形有稳定性,斜钉一根木条的窗框在未安装好之前也不会变形.
归纳
三角形的稳定性有广泛的应用,你能举出一些例子吗?
问题
钢架桥
起重机
三角形的稳定性有广泛的应用,你能举出一些例子吗?
问题
国家体育场
输电铁塔
四边形的不稳定性也有广泛的应用,你能举出一些例子吗?
问题
活动挂架
伸缩门
例 1 以下不是利用三角形稳定性的是( ).
A.在门框上斜钉一根木条
B.高架桥的三角形结构
C.伸缩衣挂
D.屋顶的三角形钢架
解析:伸缩衣挂是四边形结构,利用的是四边形的不稳定性.
C
归纳
三角形的稳定性——小性质,大用途
三角形的稳定性的实质是三角形的各边的长度被确定后,其形状不会再发生改变.现实生活中常常利用这一性质,将原本不稳定的形状转化为三角形,使之稳定.
例 2 观察下列图形,回答问题.
(1)图形中具有稳定性的是_______(只填序号);
①
②
③
④
⑤
①④⑤
例 2 观察下列图形,回答问题.
(2)对不具有稳定性的图形,请适当地添加线段,使之具有稳定性.
①
②
③
④
⑤
答案不唯一.
对于比较复杂的图形,只要使整个图形均由三角形构成,就能使整个图形具有稳定性.
归纳
三角形的稳定性
四边形
三角形
稳定性
不稳定性
三角形的稳定性与四边形的不稳定性的应用
谢谢
