13.5.2 线段垂直平分线 课件(共17张PPT) 华东师大版数学八年级上册
文档属性
| 名称 | 13.5.2 线段垂直平分线 课件(共17张PPT) 华东师大版数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 969.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-16 00:39:04 | ||
图片预览





文档简介
(共17张PPT)
华师大版八年级数学上册
第十三章 全等三角形
13.5.2 线段垂直平分线
复习回顾
1、线段是轴对称图形么?如果是轴对称图形,它的对称轴是什么?
线段是轴对称图形,对称轴是这条线段的垂直平分线。
2、什么是线段的垂直平分线?
垂直并且平分一条线段的直线称为这条线段的垂直平分线,也称为中垂线。
┓
A同学和B同学参加了一个趣味游戏,游戏规定:二人同时开始冲刺,谁先拿到奖品,奖品就归谁。为了确保比赛公平,奖品应该放在什么位置?
情境引入
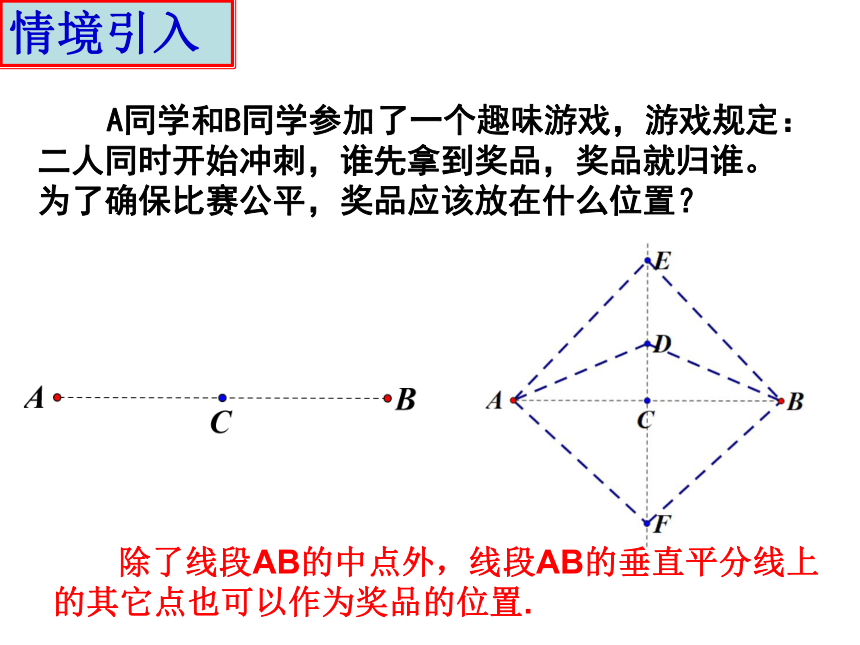
A同学和B同学参加了一个趣味游戏,游戏规定:二人同时开始冲刺,谁先拿到奖品,奖品就归谁。为了确保比赛公平,奖品应该放在什么位置?
除了线段AB的中点外,线段AB的垂直平分线上的其它点也可以作为奖品的位置.
情境引入
画一画:利用尺规作图法作出线段AB的垂直平分线MN。
探索新知
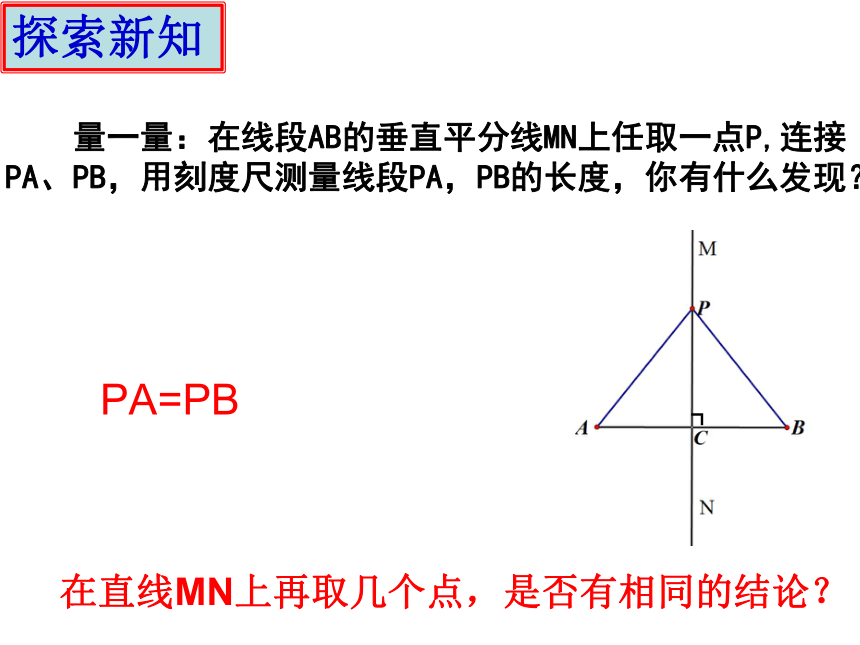
量一量:在线段AB的垂直平分线MN上任取一点P,连接PA、PB,用刻度尺测量线段PA,PB的长度,你有什么发现?
探索新知
┓
PA=PB
在直线MN上再取几个点,是否有相同的结论?
通过度量发现,在线段AB的垂直平分线MN上取其它点时,这些点到线段两端的距离也相等.
探索新知
PA=PB,DA=DB,EA=EB,FA=FB┉┉
通过以上的观察、测量、比较,你能得出什么样的猜想?
线段垂直平分线上的点到线段两端的距离相等
已知:如图,MN⊥AB,垂足为点C,AC=BC,点P是直线MN上的任意一点.
求证: PA=PB.
探索新知
┓
线段垂直平分线的性质定理
线段垂直平分线上的点到线段两端的距离相等.
总结新知
符号语言:∵ MN⊥AB,AC=BC
点P在直线MN上
∴PA=PB
┓
当堂巩固
1、如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长为( )
A.6 B.5 C.4 D.3
当堂巩固
2、如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是( )
A.12 B.13 C.14 D.15
当堂巩固
3.如图,在△ABC中,DE是AC的垂直平分线,且分别交BC、AC于点D和E,∠B=60°,∠C=25°,则∠BAD为( )
A.50° B.70° C.75° D.80°
当堂巩固
4、如图,BD⊥AC,垂足为点E,AE=CE.
求证:AB+CD=AD+BC.
当堂巩固
5、如图,已知AB比AC长2cm,BC的垂直平分线交AB于点D,交BC于点E, △ACD的周长为14cm,求AB和AC的长.
当堂巩固
6、如图,在△ABC中,AB=AC,∠A=36°,AB的中垂线DE交AC于点D,交AB于点E,下列结论:①BD平分∠ABC;②AD=BD=BC;③△BDC的周长等于AB+BC;④D是AC中点.其中正确的是_____(填序号)
拓展延伸
7、在等腰△ABC中,AB=AC,AB的垂直平分线DE与AC所在的直线相交所成的锐角是40°,则∠ABC=( )
A.40°或60° B.65°
C.25°或65° D.35°或125°
2、线段的垂直平分线的性质的应用:结合题意灵活构造等腰三角形,进而利用等腰三角形的性质;运用转化思想来求相应的边和角的大小.
1、线段的垂直平分线的性质:
线段的垂直平分线上的点到线段两端的距离相等.
┓
符号语言:∵ MN⊥AB,AC=BC
点P在直线MN上
∴PA=PB
课堂小结
华师大版八年级数学上册
第十三章 全等三角形
13.5.2 线段垂直平分线
复习回顾
1、线段是轴对称图形么?如果是轴对称图形,它的对称轴是什么?
线段是轴对称图形,对称轴是这条线段的垂直平分线。
2、什么是线段的垂直平分线?
垂直并且平分一条线段的直线称为这条线段的垂直平分线,也称为中垂线。
┓
A同学和B同学参加了一个趣味游戏,游戏规定:二人同时开始冲刺,谁先拿到奖品,奖品就归谁。为了确保比赛公平,奖品应该放在什么位置?
情境引入
A同学和B同学参加了一个趣味游戏,游戏规定:二人同时开始冲刺,谁先拿到奖品,奖品就归谁。为了确保比赛公平,奖品应该放在什么位置?
除了线段AB的中点外,线段AB的垂直平分线上的其它点也可以作为奖品的位置.
情境引入
画一画:利用尺规作图法作出线段AB的垂直平分线MN。
探索新知
量一量:在线段AB的垂直平分线MN上任取一点P,连接PA、PB,用刻度尺测量线段PA,PB的长度,你有什么发现?
探索新知
┓
PA=PB
在直线MN上再取几个点,是否有相同的结论?
通过度量发现,在线段AB的垂直平分线MN上取其它点时,这些点到线段两端的距离也相等.
探索新知
PA=PB,DA=DB,EA=EB,FA=FB┉┉
通过以上的观察、测量、比较,你能得出什么样的猜想?
线段垂直平分线上的点到线段两端的距离相等
已知:如图,MN⊥AB,垂足为点C,AC=BC,点P是直线MN上的任意一点.
求证: PA=PB.
探索新知
┓
线段垂直平分线的性质定理
线段垂直平分线上的点到线段两端的距离相等.
总结新知
符号语言:∵ MN⊥AB,AC=BC
点P在直线MN上
∴PA=PB
┓
当堂巩固
1、如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长为( )
A.6 B.5 C.4 D.3
当堂巩固
2、如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是( )
A.12 B.13 C.14 D.15
当堂巩固
3.如图,在△ABC中,DE是AC的垂直平分线,且分别交BC、AC于点D和E,∠B=60°,∠C=25°,则∠BAD为( )
A.50° B.70° C.75° D.80°
当堂巩固
4、如图,BD⊥AC,垂足为点E,AE=CE.
求证:AB+CD=AD+BC.
当堂巩固
5、如图,已知AB比AC长2cm,BC的垂直平分线交AB于点D,交BC于点E, △ACD的周长为14cm,求AB和AC的长.
当堂巩固
6、如图,在△ABC中,AB=AC,∠A=36°,AB的中垂线DE交AC于点D,交AB于点E,下列结论:①BD平分∠ABC;②AD=BD=BC;③△BDC的周长等于AB+BC;④D是AC中点.其中正确的是_____(填序号)
拓展延伸
7、在等腰△ABC中,AB=AC,AB的垂直平分线DE与AC所在的直线相交所成的锐角是40°,则∠ABC=( )
A.40°或60° B.65°
C.25°或65° D.35°或125°
2、线段的垂直平分线的性质的应用:结合题意灵活构造等腰三角形,进而利用等腰三角形的性质;运用转化思想来求相应的边和角的大小.
1、线段的垂直平分线的性质:
线段的垂直平分线上的点到线段两端的距离相等.
┓
符号语言:∵ MN⊥AB,AC=BC
点P在直线MN上
∴PA=PB
课堂小结
