15.2.1 第1课时 分式的乘除课件 人教版八年级上册 (38张PPT)
文档属性
| 名称 | 15.2.1 第1课时 分式的乘除课件 人教版八年级上册 (38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-16 07:22:59 | ||
图片预览










文档简介
(共38张PPT)
15.2.1 分式的乘除
第十五章 分 式
第1课时 分式的乘除
1.化简:
旧知回顾
2.分数的乘除法法则:
分数的乘法法则:用 作为积的分子,用
作为积的分母.
分数的除法法则:把除数的 、 颠倒位置后,与被除数 .
分子的积
分母的积
分子
分母
相乘
长方体容器的高为 ,
问题1 一个长方体容器的容积为V,底面的长为a,
宽为b,当容器内的水占容积的 时,水高多少
水面的高度为
问题情境
问题2 大拖拉机m天耕地a公顷,小拖拉机n天耕地b公顷,大拖拉机的工作效率是小拖拉机的工作效率的多少倍
大拖拉机的工作效率是 公顷/天,小拖拉机的工作效
率是 公顷/天,大拖拉机的工作效率是小拖拉机的工作效
率的( )倍.
问题情境
类比分数的计算,计算下列各题
探究新知
类比分数的运算法则,我们可以得到:
乘法法则:
分式乘分式,用分子的积作为积的分子,分母的积作为积的分母.
除法法则:
分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.
上述法则用式子表示为:
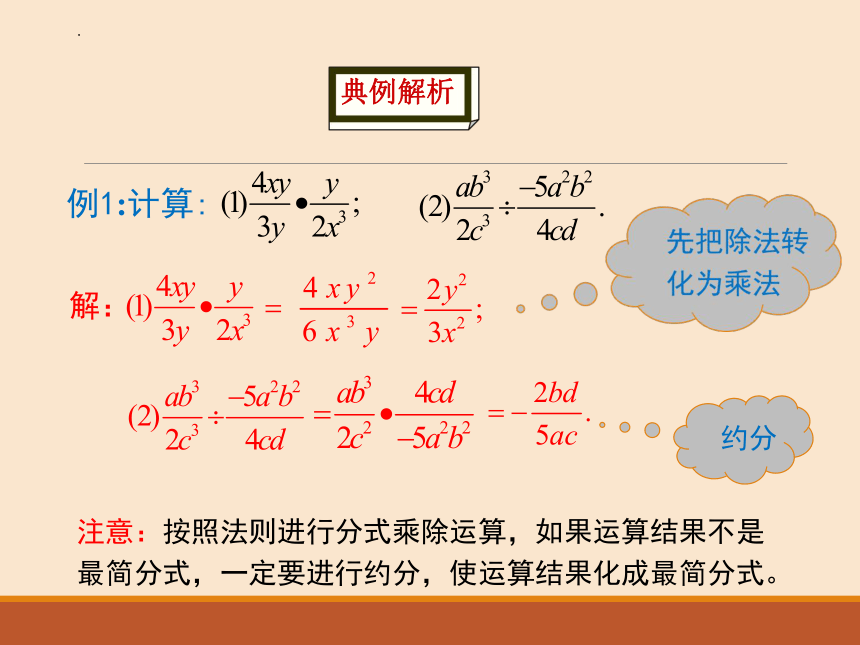
例1:计算:
解:
注意:按照法则进行分式乘除运算,如果运算结果不是最简分式,一定要进行约分,使运算结果化成最简分式。
约分
典例解析
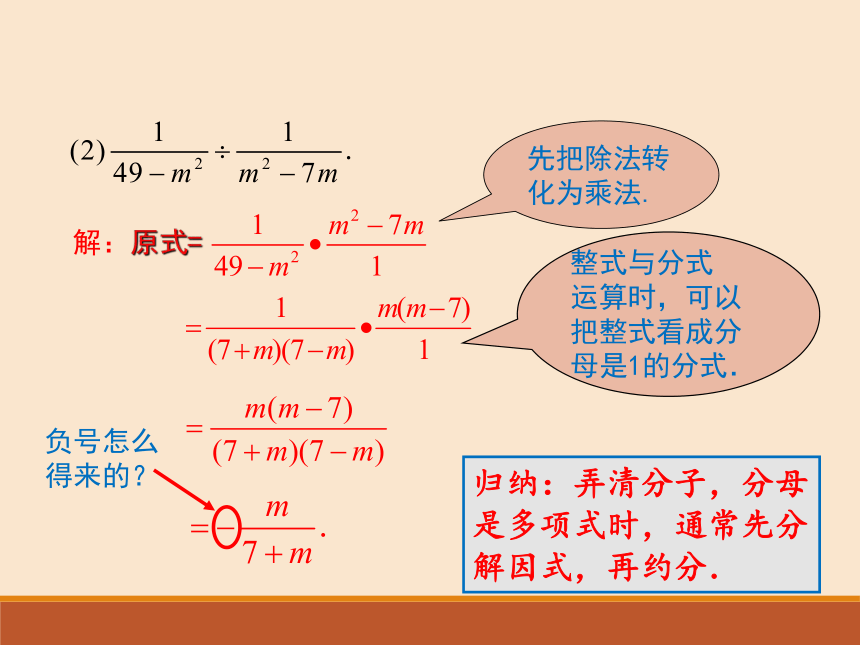
例 2 计算:
解:原式=
典例解析
整式与分式 运算时,可以把整式看成分母是1的分式.
解:原式=
负号怎么得来的?
先把除法转化为乘法.
归纳:弄清分子,分母是多项式时,通常先分解因式,再约分.
即时练习
例 “丰收1号”小麦的试验田是边长为a米的正方形减去一个边长为1米的正方形蓄水池后余下的部分, “丰收2号”小麦的试验田是边长为(a-1)米的正方形,两块试验田的小麦都收获了500千克.
(1)哪种小麦的单位面
积产量高?
(2)高的单位面积产量
是低的单位面积产量的
多少倍?
1m
am
(a-1)m
学以致用
am
1m
(a-1)m
∵a>1, 0<(a-1)2, a 2-1>0,
由图可得(a-1)2< a 2-1.
∴
解:(1)“丰收1号”小麦的试验田面积是(a 2-1)m2,单位面积产量是 kg/m2;“丰收2号”小麦的试验田面积是(a-1)2m2,单位面积产量是 kg/m2.
∴“丰收2号”小麦的单位面积产量高.
(2)
所以 “丰收2号”小麦的单位面积产量是“丰收1号”小麦的单位面积产量的 倍.
1.分式的分子、分母都是几个因式的积的形式,可先约去分子、分母的公因式,再按照法则进行计算.
2.分子或分母是多项式的按以下方法进行:
①将原分式中含同一字母的各多项式按降幂(或升幂)排列;在乘除过程中遇到整式则视其为分母为1,分子为这个整式的分式;
②把各分式中分子或分母里的多项式分解因式;
③应用分式乘除法法则进行运算;(注意:结果为最简分式或整式.)
方法总结
达标练习
B
A
D
达标练习
达标练习
甲乙两个工程队合修一条公路,已知甲工程队每天修(a2-4)米,乙工程队每天修(a-2)2米(其中a>2),甲工程队修900米所用时间是乙工程队修600米所用时间的多少倍?
答:甲工程队修900米所用时间是乙工程队修600米所用时间的 倍.
达标练习
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
回顾
相同的分数相乘
…
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
回顾
相同的分式相乘
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
乘方的意义
分式的乘法法则
探究
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
一般地,当n是正整数时,
,即
分式乘方要把分子、分母分别乘方.
分式的乘方法则
a,b分别表示分子与分母,它们可以是单项式,也可以是多项式.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
合作
分母乘方
分子乘方
化简
分式乘方时,一定要将分式加上括号,并且要将分子、分母分别乘方(单字母或数字除外).
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
分母乘方
分子乘方
正分式的任何次幂都为正,负分式的偶次幂为正,奇次幂为负.
化简
分式乘方时,若分式的分子或分母是多项式,应把分子、分母分别看作一个整体乘方.
合作
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
(1)分式乘方时,确定乘方结果符号的方法与有理数乘方确定结果符号的方法相同:正分式的任何次幂都为正,负分式的偶次幂为正,奇次幂为负;
(2)分式乘方时,一定要将分式加上括号,并且要将分子、分母分别乘方;
(3)分式乘方时,若分式的分子或分母是多项式,应把分子、分母分别看作一个整体乘方.
分式的乘方
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
做一做
计算:
(1) ; (2) .
解:(1)
(2)
抢答
;
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
括号
乘方
乘、除
数的乘除、乘方混合运算顺序
数(分式)的乘除、乘方混合运算顺序
回顾
按照从左到右的顺序进行计算;
先乘方,再乘除;
有括号的先算括号里面的.
化成最简形式.
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
例1 计算:
解:
乘除混合运算可以统一为乘法运算.
分式乘除运算的一般步骤:
(1)先把除法统一成乘法运算;
(4)结果应是最简分式.
(2)分子、分母中能分解因式的
多项式分解因式;
(3)确定分式的符号,然后约分;
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
例2 计算:
解:
式与数有相同的混合运算顺序:先乘方,再乘除.
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习1
随堂练习
(2) (3)
计算:
(1)
(2)
(3)
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习2
随堂练习
已知a=b+2021,求 的值.
解:
∵a=b+2021,∴ a – b=2021, ∴原式=2×2021=4042 .
应用新知
课堂小结
布置作业
创设情境
练习3
探究新知
巩固新知
先化简,再求值:
其中
解:原式
当 时,原式= – 4.
随堂练习
应用新知
布置作业
创设情境
探究新知
巩固新知
练习4
课堂小结
有这样一道题:计算 的值.小明同学把“ x=2”错抄成“x= –2”,但他的计算结果也正确,你说这是怎么回事?
解:原式
所以x=2或x= –2时,原式的值都等于16.
随堂练习
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
分式乘方要把分子、分母分别乘方.
分式的乘方法则
分式的乘除
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
(1)分式乘方时,确定乘方结果符号的方法与有理数乘方确定结果符号的方法相同:正分式的任何次幂都为正,负分式的偶次幂为正,奇次幂为负;
(2)分式乘方时,一定要将分式加上括号,并且要将分子、分母分别乘方;
(3)分式乘方时,若分式的分子或分母是多项式,应把分子、分母分别看作一个整体乘方.
分式的乘方
分式的乘除
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
按照从左到右的顺序进行计算;
先乘方,再乘除;
有括号的先算括号里面的;
化成最简形式.
分式的乘除、乘方混合运算顺序
分式的乘除
布置作业
教科书第139页练习1、2(2).
第146页习题3.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
15.2.1 分式的乘除
第十五章 分 式
第1课时 分式的乘除
1.化简:
旧知回顾
2.分数的乘除法法则:
分数的乘法法则:用 作为积的分子,用
作为积的分母.
分数的除法法则:把除数的 、 颠倒位置后,与被除数 .
分子的积
分母的积
分子
分母
相乘
长方体容器的高为 ,
问题1 一个长方体容器的容积为V,底面的长为a,
宽为b,当容器内的水占容积的 时,水高多少
水面的高度为
问题情境
问题2 大拖拉机m天耕地a公顷,小拖拉机n天耕地b公顷,大拖拉机的工作效率是小拖拉机的工作效率的多少倍
大拖拉机的工作效率是 公顷/天,小拖拉机的工作效
率是 公顷/天,大拖拉机的工作效率是小拖拉机的工作效
率的( )倍.
问题情境
类比分数的计算,计算下列各题
探究新知
类比分数的运算法则,我们可以得到:
乘法法则:
分式乘分式,用分子的积作为积的分子,分母的积作为积的分母.
除法法则:
分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.
上述法则用式子表示为:
例1:计算:
解:
注意:按照法则进行分式乘除运算,如果运算结果不是最简分式,一定要进行约分,使运算结果化成最简分式。
约分
典例解析
例 2 计算:
解:原式=
典例解析
整式与分式 运算时,可以把整式看成分母是1的分式.
解:原式=
负号怎么得来的?
先把除法转化为乘法.
归纳:弄清分子,分母是多项式时,通常先分解因式,再约分.
即时练习
例 “丰收1号”小麦的试验田是边长为a米的正方形减去一个边长为1米的正方形蓄水池后余下的部分, “丰收2号”小麦的试验田是边长为(a-1)米的正方形,两块试验田的小麦都收获了500千克.
(1)哪种小麦的单位面
积产量高?
(2)高的单位面积产量
是低的单位面积产量的
多少倍?
1m
am
(a-1)m
学以致用
am
1m
(a-1)m
∵a>1, 0<(a-1)2, a 2-1>0,
由图可得(a-1)2< a 2-1.
∴
解:(1)“丰收1号”小麦的试验田面积是(a 2-1)m2,单位面积产量是 kg/m2;“丰收2号”小麦的试验田面积是(a-1)2m2,单位面积产量是 kg/m2.
∴“丰收2号”小麦的单位面积产量高.
(2)
所以 “丰收2号”小麦的单位面积产量是“丰收1号”小麦的单位面积产量的 倍.
1.分式的分子、分母都是几个因式的积的形式,可先约去分子、分母的公因式,再按照法则进行计算.
2.分子或分母是多项式的按以下方法进行:
①将原分式中含同一字母的各多项式按降幂(或升幂)排列;在乘除过程中遇到整式则视其为分母为1,分子为这个整式的分式;
②把各分式中分子或分母里的多项式分解因式;
③应用分式乘除法法则进行运算;(注意:结果为最简分式或整式.)
方法总结
达标练习
B
A
D
达标练习
达标练习
甲乙两个工程队合修一条公路,已知甲工程队每天修(a2-4)米,乙工程队每天修(a-2)2米(其中a>2),甲工程队修900米所用时间是乙工程队修600米所用时间的多少倍?
答:甲工程队修900米所用时间是乙工程队修600米所用时间的 倍.
达标练习
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
回顾
相同的分数相乘
…
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
回顾
相同的分式相乘
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
乘方的意义
分式的乘法法则
探究
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
一般地,当n是正整数时,
,即
分式乘方要把分子、分母分别乘方.
分式的乘方法则
a,b分别表示分子与分母,它们可以是单项式,也可以是多项式.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
合作
分母乘方
分子乘方
化简
分式乘方时,一定要将分式加上括号,并且要将分子、分母分别乘方(单字母或数字除外).
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
分母乘方
分子乘方
正分式的任何次幂都为正,负分式的偶次幂为正,奇次幂为负.
化简
分式乘方时,若分式的分子或分母是多项式,应把分子、分母分别看作一个整体乘方.
合作
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
(1)分式乘方时,确定乘方结果符号的方法与有理数乘方确定结果符号的方法相同:正分式的任何次幂都为正,负分式的偶次幂为正,奇次幂为负;
(2)分式乘方时,一定要将分式加上括号,并且要将分子、分母分别乘方;
(3)分式乘方时,若分式的分子或分母是多项式,应把分子、分母分别看作一个整体乘方.
分式的乘方
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
做一做
计算:
(1) ; (2) .
解:(1)
(2)
抢答
;
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
括号
乘方
乘、除
数的乘除、乘方混合运算顺序
数(分式)的乘除、乘方混合运算顺序
回顾
按照从左到右的顺序进行计算;
先乘方,再乘除;
有括号的先算括号里面的.
化成最简形式.
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
例1 计算:
解:
乘除混合运算可以统一为乘法运算.
分式乘除运算的一般步骤:
(1)先把除法统一成乘法运算;
(4)结果应是最简分式.
(2)分子、分母中能分解因式的
多项式分解因式;
(3)确定分式的符号,然后约分;
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
例2 计算:
解:
式与数有相同的混合运算顺序:先乘方,再乘除.
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习1
随堂练习
(2) (3)
计算:
(1)
(2)
(3)
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习2
随堂练习
已知a=b+2021,求 的值.
解:
∵a=b+2021,∴ a – b=2021, ∴原式=2×2021=4042 .
应用新知
课堂小结
布置作业
创设情境
练习3
探究新知
巩固新知
先化简,再求值:
其中
解:原式
当 时,原式= – 4.
随堂练习
应用新知
布置作业
创设情境
探究新知
巩固新知
练习4
课堂小结
有这样一道题:计算 的值.小明同学把“ x=2”错抄成“x= –2”,但他的计算结果也正确,你说这是怎么回事?
解:原式
所以x=2或x= –2时,原式的值都等于16.
随堂练习
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
分式乘方要把分子、分母分别乘方.
分式的乘方法则
分式的乘除
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
(1)分式乘方时,确定乘方结果符号的方法与有理数乘方确定结果符号的方法相同:正分式的任何次幂都为正,负分式的偶次幂为正,奇次幂为负;
(2)分式乘方时,一定要将分式加上括号,并且要将分子、分母分别乘方;
(3)分式乘方时,若分式的分子或分母是多项式,应把分子、分母分别看作一个整体乘方.
分式的乘方
分式的乘除
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
按照从左到右的顺序进行计算;
先乘方,再乘除;
有括号的先算括号里面的;
化成最简形式.
分式的乘除、乘方混合运算顺序
分式的乘除
布置作业
教科书第139页练习1、2(2).
第146页习题3.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
