第二章 一元二次方程 复习课(共23张PPT) 北师大版九年级上册数学
文档属性
| 名称 | 第二章 一元二次方程 复习课(共23张PPT) 北师大版九年级上册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 819.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-16 00:00:00 | ||
图片预览




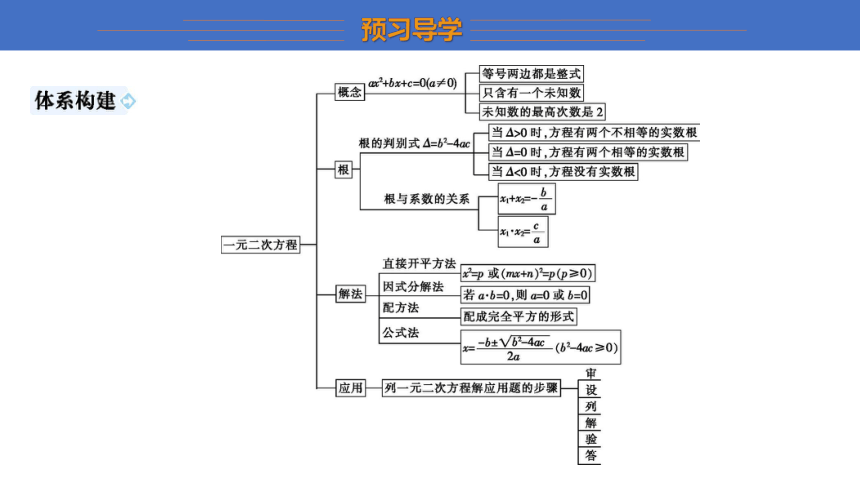




文档简介
(共23张PPT)
第二章 一元二次方程
第二章 复习课
1.知道一元二次方程的概念,掌握本章所学的解一元二次方程的配方法、公式法、分解因式法,会合理选择方法解具体的一元二次方程,并在解方程的过程中体会转化等数学思想.
2.会用根的判别式判别一元二次方程的根的情况,会用根与系数的关系解决问题.
3.利用一元二次方程的有关知识解决实际问题,并能根据具体问题的实际意义检验结果的合理性.
◎重点:掌握一元二次方程的根的判别式,选择合适的方法解一元二次方程.
激趣导入
知识在于积累,能力在于训练,这节课我们一起来重点回顾一元二次方程的概念、解法和应用,查缺补漏,以求厚积薄发.希望人人达标过关!
核心梳理
1.一元二次方程的定义理解应抓住其本质,它必须同时满足这样的三个条件:(1)是 整式 方程;(2)只含 一个 未知数;(3)未知数的最高次数是 2 .一个方程是否为一元二次方程,是对整理化简之后而言的,如:x3-x(x2-2x+1)-2=0,化简后为 2x2-x-2=0 ,是一元 二 次方程.
整式
一个
2
2x2-x-2=0
二
2.我们把 ax2+bx+c=0(a≠0) 叫做一元二次方程的一般式,其中 ax2 、 bx 、 c 分别叫做二次项、一次项、常数项, a 、 b 分别叫做二次项系数,一次项系数.需要注意的是(1)“a≠0”是一般式的重要组成部分,不可遗漏,但可以缺少一次项和常数项,即b、c均可以为0;(2)方程的一边必须为0.
ax2+bx+c=0(a≠0)
ax2
bx
c
a
b
3.使一元二次方程 左右两边相等 的未知数的值叫做一元二次方程的解(或根).
注意:(1)一元二次方程在实数范围内可以无解,但是有解就一定有 两 个解(相等或不等);(2)可用代入法检验一个数是否是一元二次方程的解,以及求待定常数.
左右两边相等
两
4. 一元二次方程的解法有四种:(1) 直接开平方法 ;(2) 分解因式法 ;(3) 配方法 ;(4) 公式法 .要根据方程的特点灵活选择方法,其中公式法是通法,可以解任何一个一元二次方程.
直接开平方法
分解因式法
配方法
公式法
5.一元二次方程ax2+bx+c=0(a≠0)根的情况可以由 b2-4ac 的值来确定,因此,我们把 b2-4ac 叫做一元二次方程根的判别式,用符号“Δ”表示.Δ>0,方程有 两个不相等 的实数根;Δ=0,方程有 两个相等 的实数根;Δ<0,方程 没有 实数根.
b2-
4ac
b2-4ac
两个不相等
两个相等
没有
6.一元二次方程的根与系数的关系:若ax2+bx+c=0(a≠0)的两个根是x1、x2,则x1+x2= - ,x1x2= .需要注意的是一元二次方程有实数根是存在以上关系的必要前提.
-
在复习本章知识时,建议注重知识网络图的使用,可以让学生阅读,不仅是看网络图,还要引导学生向同伴说出一元二次方程的一般形式、解的方法等,教师要随时进行错误纠正,或者学生自己动手画知识网络图.
·导学建议·
一元二次方程的定义
1.下列方程中一元二次方程的个数是( B )
①2x-3=x2+2x-3;②ax2+bx+c=0;③(x+2)(x-2)=(x+1)2;④x+=1;⑤(x+1)(x+2)=2x2-3.
A.1 B.2 C.3 D.4
B
2.(1)将方程3x2=5x+2化为一元二次方程的一般形式为 3x2-5x-2=0 .
(2)一元二次方程2x2+4x-1=0的二次项系数、一次项系数及常数项之和为 5 .
3x2-5x-2=0
5
一元二次方程的解法
3.用不同的方法解方程:4x2+8x+1=0.
解:本题可用公式法或配方法求解,
答案:x=-1±.
4.方程(x-1)2=4的解是 x1=3,x2=-1 .
x1=3,x2=-1
方法归纳交流 在具体解方程时,要根据题目的特点,选择适当的方法求解.通常顺序为先特殊后一般.即直接开平方法→分解因式法→公式法.公式法和配方法是通法.
一元二次方程根的判别式
5.若关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根,则k的取值范围是( B )
A.k>-1 B.k>-1且k≠0
C.k<1 D.k<1且k≠0
B
一元二次方程根与系数的关系
6.已知2-是一元二次方程x2-4x+c=0的一个根,则c= -1 .
-1
一元二次方程的应用
7.有一批图形计算器,原售价为每台800元,在甲、乙两家公司销售.甲公司用如下方法促销:买一台单价为780元,买两台每台都为760元,依此类推,即每多买一台时所买各台单价均再减20元,但最低不能低于每台440元.乙公司一律按原售价的75%促销.某单位需购买一批图形计算器.
(1)若此单位需购买6台图形计算器,应去哪家公司购买花费较少?
(2)若此单位恰好花费7500元,在同一家公司购买了一定数量的图形计算器,请问是在哪家公司购买的,数量是多少?
解:(1)在甲公司购买6台图形计算器需要用6×(800-20×6)=4080(元);在乙公司购买需要用75%×800×6=3600(元)<4080(元).应去乙公司购买.
(2)设该单位买x台,若在甲公司购买,则需要花费x(800-20x)元;若在乙公司购买,则需要花费75%×800x=600x元.
①若该单位是在甲公司花费7500元购买的图形计算器,则有x(800-20x)=7500,解之得x1=15,x2=25.
当x=15时,每台单价为800-20×15=500>440,符合题意,
当x=25时,每台单价为800-20×25=300<440,不符合题意,舍去.
②若该单位是在乙公司花费7500元购买的图形计算器,则有600x=7500,解之得x=12.5,不符合题意,舍去.
故该单位是在甲公司购买的图形计算器,买了15台.
春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准:
如果人数不超过25人,人均旅游费用为1000元.
如果人数超过25人,每增加1人,人均旅游费用降低20元,但不得低于700元.
某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
解:设该单位这次共有x名员工去天水湾风景区旅游.
因为1000×25=25000<27000,所以员工人数一定超过25人,
可得方程[1000-20(x-25)]x=27000.
解得x1=45,x2=30.
当x1=45时,1000-20(x-25)=600<700,故舍去x1;
当x2=30时,1000-20(x-25)=900>700,符合题意.
答:该单位这次共有30名员工去天水湾风景区旅游.
第二章 一元二次方程
第二章 复习课
1.知道一元二次方程的概念,掌握本章所学的解一元二次方程的配方法、公式法、分解因式法,会合理选择方法解具体的一元二次方程,并在解方程的过程中体会转化等数学思想.
2.会用根的判别式判别一元二次方程的根的情况,会用根与系数的关系解决问题.
3.利用一元二次方程的有关知识解决实际问题,并能根据具体问题的实际意义检验结果的合理性.
◎重点:掌握一元二次方程的根的判别式,选择合适的方法解一元二次方程.
激趣导入
知识在于积累,能力在于训练,这节课我们一起来重点回顾一元二次方程的概念、解法和应用,查缺补漏,以求厚积薄发.希望人人达标过关!
核心梳理
1.一元二次方程的定义理解应抓住其本质,它必须同时满足这样的三个条件:(1)是 整式 方程;(2)只含 一个 未知数;(3)未知数的最高次数是 2 .一个方程是否为一元二次方程,是对整理化简之后而言的,如:x3-x(x2-2x+1)-2=0,化简后为 2x2-x-2=0 ,是一元 二 次方程.
整式
一个
2
2x2-x-2=0
二
2.我们把 ax2+bx+c=0(a≠0) 叫做一元二次方程的一般式,其中 ax2 、 bx 、 c 分别叫做二次项、一次项、常数项, a 、 b 分别叫做二次项系数,一次项系数.需要注意的是(1)“a≠0”是一般式的重要组成部分,不可遗漏,但可以缺少一次项和常数项,即b、c均可以为0;(2)方程的一边必须为0.
ax2+bx+c=0(a≠0)
ax2
bx
c
a
b
3.使一元二次方程 左右两边相等 的未知数的值叫做一元二次方程的解(或根).
注意:(1)一元二次方程在实数范围内可以无解,但是有解就一定有 两 个解(相等或不等);(2)可用代入法检验一个数是否是一元二次方程的解,以及求待定常数.
左右两边相等
两
4. 一元二次方程的解法有四种:(1) 直接开平方法 ;(2) 分解因式法 ;(3) 配方法 ;(4) 公式法 .要根据方程的特点灵活选择方法,其中公式法是通法,可以解任何一个一元二次方程.
直接开平方法
分解因式法
配方法
公式法
5.一元二次方程ax2+bx+c=0(a≠0)根的情况可以由 b2-4ac 的值来确定,因此,我们把 b2-4ac 叫做一元二次方程根的判别式,用符号“Δ”表示.Δ>0,方程有 两个不相等 的实数根;Δ=0,方程有 两个相等 的实数根;Δ<0,方程 没有 实数根.
b2-
4ac
b2-4ac
两个不相等
两个相等
没有
6.一元二次方程的根与系数的关系:若ax2+bx+c=0(a≠0)的两个根是x1、x2,则x1+x2= - ,x1x2= .需要注意的是一元二次方程有实数根是存在以上关系的必要前提.
-
在复习本章知识时,建议注重知识网络图的使用,可以让学生阅读,不仅是看网络图,还要引导学生向同伴说出一元二次方程的一般形式、解的方法等,教师要随时进行错误纠正,或者学生自己动手画知识网络图.
·导学建议·
一元二次方程的定义
1.下列方程中一元二次方程的个数是( B )
①2x-3=x2+2x-3;②ax2+bx+c=0;③(x+2)(x-2)=(x+1)2;④x+=1;⑤(x+1)(x+2)=2x2-3.
A.1 B.2 C.3 D.4
B
2.(1)将方程3x2=5x+2化为一元二次方程的一般形式为 3x2-5x-2=0 .
(2)一元二次方程2x2+4x-1=0的二次项系数、一次项系数及常数项之和为 5 .
3x2-5x-2=0
5
一元二次方程的解法
3.用不同的方法解方程:4x2+8x+1=0.
解:本题可用公式法或配方法求解,
答案:x=-1±.
4.方程(x-1)2=4的解是 x1=3,x2=-1 .
x1=3,x2=-1
方法归纳交流 在具体解方程时,要根据题目的特点,选择适当的方法求解.通常顺序为先特殊后一般.即直接开平方法→分解因式法→公式法.公式法和配方法是通法.
一元二次方程根的判别式
5.若关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根,则k的取值范围是( B )
A.k>-1 B.k>-1且k≠0
C.k<1 D.k<1且k≠0
B
一元二次方程根与系数的关系
6.已知2-是一元二次方程x2-4x+c=0的一个根,则c= -1 .
-1
一元二次方程的应用
7.有一批图形计算器,原售价为每台800元,在甲、乙两家公司销售.甲公司用如下方法促销:买一台单价为780元,买两台每台都为760元,依此类推,即每多买一台时所买各台单价均再减20元,但最低不能低于每台440元.乙公司一律按原售价的75%促销.某单位需购买一批图形计算器.
(1)若此单位需购买6台图形计算器,应去哪家公司购买花费较少?
(2)若此单位恰好花费7500元,在同一家公司购买了一定数量的图形计算器,请问是在哪家公司购买的,数量是多少?
解:(1)在甲公司购买6台图形计算器需要用6×(800-20×6)=4080(元);在乙公司购买需要用75%×800×6=3600(元)<4080(元).应去乙公司购买.
(2)设该单位买x台,若在甲公司购买,则需要花费x(800-20x)元;若在乙公司购买,则需要花费75%×800x=600x元.
①若该单位是在甲公司花费7500元购买的图形计算器,则有x(800-20x)=7500,解之得x1=15,x2=25.
当x=15时,每台单价为800-20×15=500>440,符合题意,
当x=25时,每台单价为800-20×25=300<440,不符合题意,舍去.
②若该单位是在乙公司花费7500元购买的图形计算器,则有600x=7500,解之得x=12.5,不符合题意,舍去.
故该单位是在甲公司购买的图形计算器,买了15台.
春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准:
如果人数不超过25人,人均旅游费用为1000元.
如果人数超过25人,每增加1人,人均旅游费用降低20元,但不得低于700元.
某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
解:设该单位这次共有x名员工去天水湾风景区旅游.
因为1000×25=25000<27000,所以员工人数一定超过25人,
可得方程[1000-20(x-25)]x=27000.
解得x1=45,x2=30.
当x1=45时,1000-20(x-25)=600<700,故舍去x1;
当x2=30时,1000-20(x-25)=900>700,符合题意.
答:该单位这次共有30名员工去天水湾风景区旅游.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
