13.5.2线段垂直平分线课件 华东师大版八年级数学上册(19张PPT)
文档属性
| 名称 | 13.5.2线段垂直平分线课件 华东师大版八年级数学上册(19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-16 07:34:19 | ||
图片预览




文档简介
(共19张PPT)
情境引入
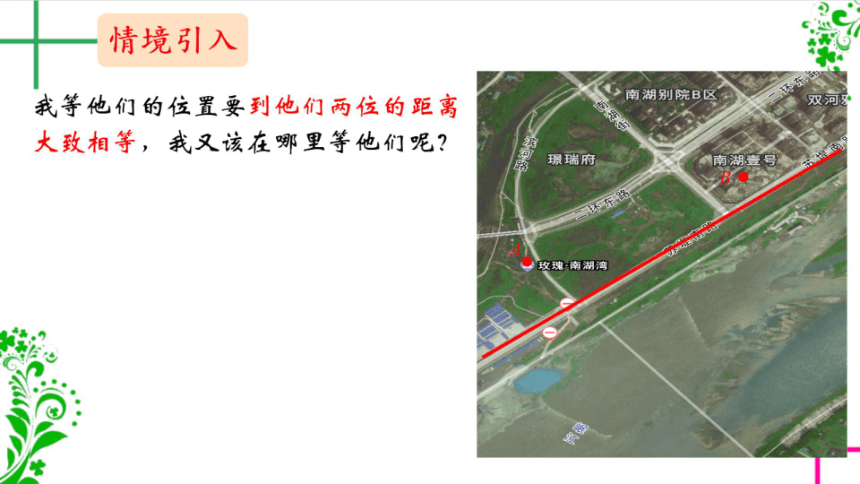
法国文学家伏尔泰说:”生命在于
>南湖别院B区
双河
运动”。跑步是大家都热爱的运动,今
河
路
璟瑞府
南湖壹号
晚我准备约两位好友在苏堤南路跑步
,两位好友让我到了后在苏堤南路上
环东路
等他们,还要求我等他们的位置要离
玫瑰南湖湾
他们两位的距离之和最短,我应该在
哪里等他们呢?
肖扇
情境引入
东
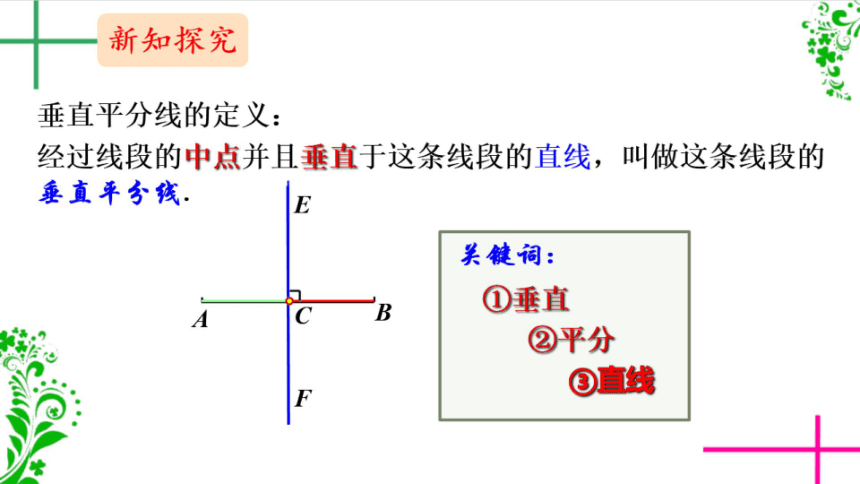
我等他们的位置要到他们两位的距离
>南湖别院B区
双河
大致相等,我又该在哪里等他们呢?
河
璟瑞府
南湖壹号
南
R
二环东路
玫瑰南湖湾
华师版数学八年级上册
13.5.2
线段垂直平分线
新知探究
画一画:作线段AB,过线段AB的中点C作垂线EF
A
B
新知探究
垂直平分线的定义:
经过线段的中点并且垂直于这条线段的直线,叫做这条线段的
垂直年分我。
关健祠:
①垂直
②平分
③直线
自主探究
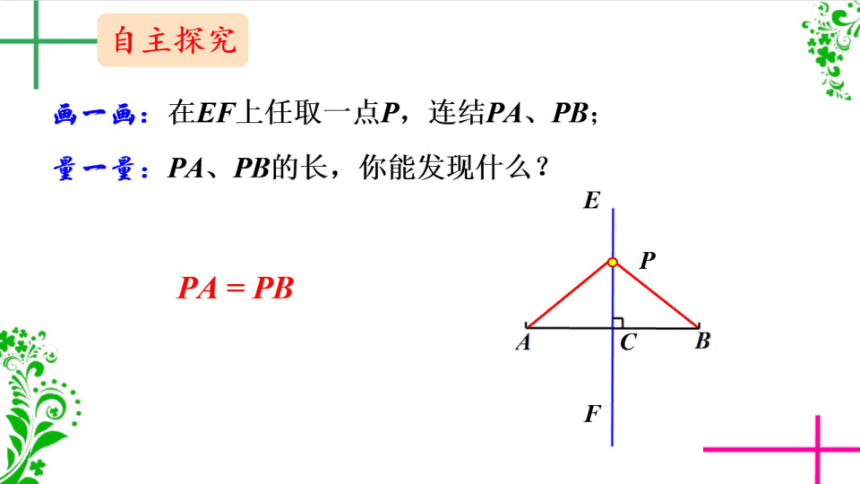
画一画:在EF上任取一点P,连结PA、PB;
量一量:PA、PB的长,你能发现什么?
E
PA=PB
y
B
F
提出猜想
四
线段
上的点到线段两个端点的距离
获得定理
线段垂直平分线上的点到线段两个端点的距离相等:
已知:如图,直线l⊥AB,垂足为C,AC=CB,点P在1上.
求证:PA=PB
证明:,1⊥AB
【符号语言】
∴.∠ACP=∠BCP=90
.1⊥AB,AC=BC
在△ACP和△BCP中
(1垂直平分线段AB)
AC=BC
B
..PA=PB
∠ACP=∠BCP
CP-CP
判断和证明两条线段相等
∴.△ACP2△BCP(SA.S.)
∴PA=PB
解决问题
我等他们的位置要到他们两位的距离
>南湖别院B区
双河
大致相等,我又该在哪里等他们呢?
河
璟瑞府
南湖壹号
盆南
二环东
文瑰南湖湾
运用定理
例1.如图,在△ABC中,AB的垂直平分线交AC于点E.
①若AE=5cm,则BE=
5cm
②若∠A=40°则∠ABE=40°.
③若AC=8cm,BC=6cm,则
△BCE周长为
14cm
提出猜想
线段垂直平分线的性质定理,条件和结论反过来会有什么结果呢?
>
写出性质定理及其逆命题的条件和结论,你有什么发现?
条件
结论
一个点在线段的垂
这个点到线段两端
性质定理
直平分线上
的距离相等
一个点到线段两端
这个点在线段的垂
逆命题
的距离相等
直平分线上
思
这个逆命题是不是一个真命题?你能证明吗?
证明猜想
到线段两端距离相等的点在这条线段的垂直平分线上.
己知:如图,PA=PB,
求证:点P在线段AB的垂直平分线上。
证法1:过点P作PCLAB于点C
.PC⊥AB
.∴.∠PCA=∠PCB=90°
B
又.PA=PB,PC=PC
.'.Rt△PCA≌Rt△PCB
(H)
.∴.CA=CB
作出垂直
.∴PC垂直平分AB
证明年分
即点P在线段AB的垂直平分线上
情境引入
法国文学家伏尔泰说:”生命在于
>南湖别院B区
双河
运动”。跑步是大家都热爱的运动,今
河
路
璟瑞府
南湖壹号
晚我准备约两位好友在苏堤南路跑步
,两位好友让我到了后在苏堤南路上
环东路
等他们,还要求我等他们的位置要离
玫瑰南湖湾
他们两位的距离之和最短,我应该在
哪里等他们呢?
肖扇
情境引入
东
我等他们的位置要到他们两位的距离
>南湖别院B区
双河
大致相等,我又该在哪里等他们呢?
河
璟瑞府
南湖壹号
南
R
二环东路
玫瑰南湖湾
华师版数学八年级上册
13.5.2
线段垂直平分线
新知探究
画一画:作线段AB,过线段AB的中点C作垂线EF
A
B
新知探究
垂直平分线的定义:
经过线段的中点并且垂直于这条线段的直线,叫做这条线段的
垂直年分我。
关健祠:
①垂直
②平分
③直线
自主探究
画一画:在EF上任取一点P,连结PA、PB;
量一量:PA、PB的长,你能发现什么?
E
PA=PB
y
B
F
提出猜想
四
线段
上的点到线段两个端点的距离
获得定理
线段垂直平分线上的点到线段两个端点的距离相等:
已知:如图,直线l⊥AB,垂足为C,AC=CB,点P在1上.
求证:PA=PB
证明:,1⊥AB
【符号语言】
∴.∠ACP=∠BCP=90
.1⊥AB,AC=BC
在△ACP和△BCP中
(1垂直平分线段AB)
AC=BC
B
..PA=PB
∠ACP=∠BCP
CP-CP
判断和证明两条线段相等
∴.△ACP2△BCP(SA.S.)
∴PA=PB
解决问题
我等他们的位置要到他们两位的距离
>南湖别院B区
双河
大致相等,我又该在哪里等他们呢?
河
璟瑞府
南湖壹号
盆南
二环东
文瑰南湖湾
运用定理
例1.如图,在△ABC中,AB的垂直平分线交AC于点E.
①若AE=5cm,则BE=
5cm
②若∠A=40°则∠ABE=40°.
③若AC=8cm,BC=6cm,则
△BCE周长为
14cm
提出猜想
线段垂直平分线的性质定理,条件和结论反过来会有什么结果呢?
>
写出性质定理及其逆命题的条件和结论,你有什么发现?
条件
结论
一个点在线段的垂
这个点到线段两端
性质定理
直平分线上
的距离相等
一个点到线段两端
这个点在线段的垂
逆命题
的距离相等
直平分线上
思
这个逆命题是不是一个真命题?你能证明吗?
证明猜想
到线段两端距离相等的点在这条线段的垂直平分线上.
己知:如图,PA=PB,
求证:点P在线段AB的垂直平分线上。
证法1:过点P作PCLAB于点C
.PC⊥AB
.∴.∠PCA=∠PCB=90°
B
又.PA=PB,PC=PC
.'.Rt△PCA≌Rt△PCB
(H)
.∴.CA=CB
作出垂直
.∴PC垂直平分AB
证明年分
即点P在线段AB的垂直平分线上
