第三章 概率的进一步认识 课件 北师大版数学九年级上册(20张PPT)
文档属性
| 名称 | 第三章 概率的进一步认识 课件 北师大版数学九年级上册(20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-16 08:00:16 | ||
图片预览








文档简介
(共20张PPT)
第三章 概率的进一步认识
第三章 复习课
1.回顾本章的内容,梳理本章的知识结构,建立有关概率知识的框架图.
2.知道求概率的一般方法——树状图和列表法.
3.知道试验频率与理论概率的关系;会合理运用概率的思想,解决生活中的实际问题.
◎重点:会用树状图或列表法计算简单事件的概率,以及用试验或模拟试验的方法估计复杂事件发生的概率.
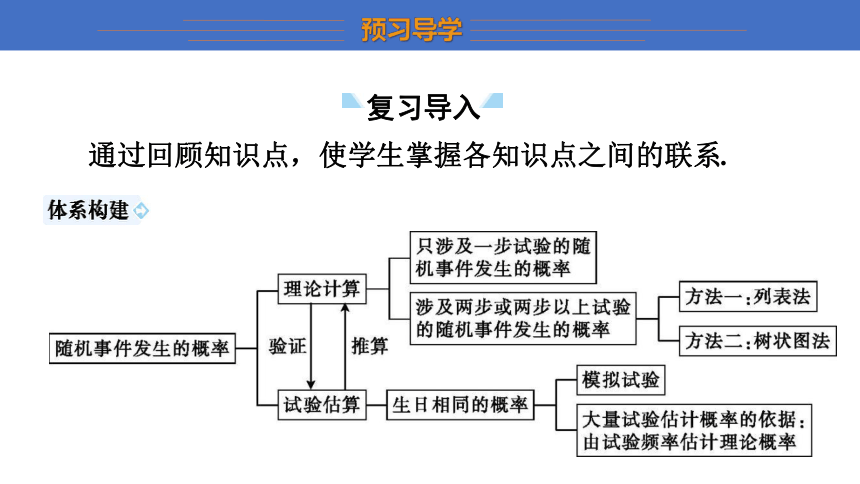
复习导入
通过回顾知识点,使学生掌握各知识点之间的联系.
核心梳理
1.当试验次数很大时,一个随机事件发生的频率总是稳定于相应的 理论概率 .
概率
2.频率与概率的关系:
(1)概率反映了一个随机事件发生的可能性的大小,而频率只有在大量重复试验的前提下才可近似地作为这个事件的概率;
(2)概率是频率的 稳定值 ,而频率是概率的 近似值 .
稳定值
近似
值
3.树状图法或列表法求随机事件的概率.
(1)用树状图法求概率比较直观,求解时要注意事件发生的顺序.当一次试验要涉及3个或更多的因素时, 列表法 就显得无能为力,此时可选用树状图法来确定事件的概率.
列表法
(2)对于一类可能出现的结果多而杂的随机事件,用树状图来描述比较复杂或难以画出图形时,通常采用列表法分析可能出现的一切结果,比较简捷、明快.但用列表法计算概率往往是 两次操作作为一次实验(例如摸扑克牌两次),或者在事件中有 两个并列的条件(例如两个转盘),在这种情况下,我们往往将其中的一次操作或条件作为 横 列,另一次操作或条件作为 纵 列,列出表格.
横
纵
当一次试验中要涉及两个因素,并且可能出现的结果数目较多时,用列表法.
(3)用树状图或表格求概率的关键:
①各种情况出现的可能性 一定要相同 ;
②P(A)=;
③在统计各种情况出现的次数和某一事件发生的次数时,要做到不重不漏.
一定要相同
4.估计总体数目.
通过试验法估计总体数目的方法:(1) 抽取 法估算总体数目;(2)用 放入 法估算总体数目.
抽取
放入
·导学建议·
本节可通过问题的形式引导学生,梳理知识结构,重点关注以下几个问题:(1)频率与概率的区别;(2)计算概率的两种方法;(3)概率与统计之间的内在的联系.
随机事件的概率计算
1.某市体育中考现场考试内容有三项:50米跑为必测项目,另在立定跳远、实心球(二选一)和坐位体前屈、1分钟跳绳(二选一)中选择两项.
(1)每位考生有 种选择方案;
(2)用画树状图或列表的方法求小明与小刚选择同种方案的概率.(友情提醒:各种方案用A、B、C、……或①、②、③、……符号来代表可简化解答过程)
解:(1)4.
(2)把4种方案分别列为:A:立定跳远、坐位体前屈;B:实心球、1分钟跳绳;C:立定跳远、1分钟跳绳;D:实心球、坐位体前屈;
画树状图如图所示:
∴小明与小刚选择同种方案的概率=.
∴小明与小刚选择同种方案的概率=.
小国同学的父亲参加旅游团到某地旅游,准备买某种礼物送给小国.据了解,沿旅游线路依次有A、B、C三个地点可以买到此种礼物,其质量相当,价格各不相同,但不知哪家更便宜.由于时间关系,随团旅游车不会掉头行驶.
(1)若到A处就购买,写出买到最低价格礼物的概率.
(2)小国同学的父亲认为,如果到A处不买,到B处发现比A处便宜就马上购买,否则到C处购买,这样更有希望买到最低价格的礼物.这个想法是否正确?试通过树状图分析说明.
解:(1)∵在每一处都有价格最低,最高,较高的可能,
∴P(A处买到最低价格礼物)=.
(2)作出树状图如下:
由树状图可知P购到最低价格礼物==.
∵>,∴他的想法是正确的.
由树状图可知P(购到最低价格礼物)==.
∵>,∴他的想法是正确的.
依据概率确定数量
2.在围棋盒中有x颗白色棋子和y颗黑色棋子,从盒中随机取出一颗棋子,取得白色棋子的概率是.若再往盒中放进6颗黑色棋子,取得白色棋子的概率是,则原来盒中有白色棋子 4 颗.
4
利用频率估计概率,估计总体数目
3.某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了如图所示的统计图,根据统计图提供的信息解决下列问题:
(1)这种树苗成活的频率稳定在 0.9 ,成活的概率估计值为 0.9 ;
(2)该地区已经移植这种树苗5万棵.
①估计这种树苗成活 4.5 万棵;
②如果该地区计划成活18万棵这种树苗,那么还需移植这种树苗约 15 万棵.
0.9
0.9
4.5
15
4.王强与李刚两位同学在学习“概率”时,做抛骰子(均匀正方体形状)试验,他们共抛了54次,出现向上点数的次数如下表:
向上点数 1 2 3 4 5 6
出现次数 6 9 5 8 16 10
(1)出现向上点数为3的频率为 ,出现向上点数为5的频率为 ;
(2)王强说:“根据试验,一次试验中出现向上点数为5的概率最大.”
李刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”
请判断王强和李刚说法的对错;
(3)如果王强与李刚各抛一枚骰子,则出现向上点数之和为3的倍数的概率为 .
解:(1);.
(2)因为抛一次骰子出现点数1,2,3,4,5,6向上具有等可能性,所以王强的说法不对,虽然抛54次出现点数6向上的频数是,但只抛54次的频率不一定等于概率,因为抛一次骰子,点数6向上的概率是,所以李刚的说法也不正确.
(3).
第三章 概率的进一步认识
第三章 复习课
1.回顾本章的内容,梳理本章的知识结构,建立有关概率知识的框架图.
2.知道求概率的一般方法——树状图和列表法.
3.知道试验频率与理论概率的关系;会合理运用概率的思想,解决生活中的实际问题.
◎重点:会用树状图或列表法计算简单事件的概率,以及用试验或模拟试验的方法估计复杂事件发生的概率.
复习导入
通过回顾知识点,使学生掌握各知识点之间的联系.
核心梳理
1.当试验次数很大时,一个随机事件发生的频率总是稳定于相应的 理论概率 .
概率
2.频率与概率的关系:
(1)概率反映了一个随机事件发生的可能性的大小,而频率只有在大量重复试验的前提下才可近似地作为这个事件的概率;
(2)概率是频率的 稳定值 ,而频率是概率的 近似值 .
稳定值
近似
值
3.树状图法或列表法求随机事件的概率.
(1)用树状图法求概率比较直观,求解时要注意事件发生的顺序.当一次试验要涉及3个或更多的因素时, 列表法 就显得无能为力,此时可选用树状图法来确定事件的概率.
列表法
(2)对于一类可能出现的结果多而杂的随机事件,用树状图来描述比较复杂或难以画出图形时,通常采用列表法分析可能出现的一切结果,比较简捷、明快.但用列表法计算概率往往是 两次操作作为一次实验(例如摸扑克牌两次),或者在事件中有 两个并列的条件(例如两个转盘),在这种情况下,我们往往将其中的一次操作或条件作为 横 列,另一次操作或条件作为 纵 列,列出表格.
横
纵
当一次试验中要涉及两个因素,并且可能出现的结果数目较多时,用列表法.
(3)用树状图或表格求概率的关键:
①各种情况出现的可能性 一定要相同 ;
②P(A)=;
③在统计各种情况出现的次数和某一事件发生的次数时,要做到不重不漏.
一定要相同
4.估计总体数目.
通过试验法估计总体数目的方法:(1) 抽取 法估算总体数目;(2)用 放入 法估算总体数目.
抽取
放入
·导学建议·
本节可通过问题的形式引导学生,梳理知识结构,重点关注以下几个问题:(1)频率与概率的区别;(2)计算概率的两种方法;(3)概率与统计之间的内在的联系.
随机事件的概率计算
1.某市体育中考现场考试内容有三项:50米跑为必测项目,另在立定跳远、实心球(二选一)和坐位体前屈、1分钟跳绳(二选一)中选择两项.
(1)每位考生有 种选择方案;
(2)用画树状图或列表的方法求小明与小刚选择同种方案的概率.(友情提醒:各种方案用A、B、C、……或①、②、③、……符号来代表可简化解答过程)
解:(1)4.
(2)把4种方案分别列为:A:立定跳远、坐位体前屈;B:实心球、1分钟跳绳;C:立定跳远、1分钟跳绳;D:实心球、坐位体前屈;
画树状图如图所示:
∴小明与小刚选择同种方案的概率=.
∴小明与小刚选择同种方案的概率=.
小国同学的父亲参加旅游团到某地旅游,准备买某种礼物送给小国.据了解,沿旅游线路依次有A、B、C三个地点可以买到此种礼物,其质量相当,价格各不相同,但不知哪家更便宜.由于时间关系,随团旅游车不会掉头行驶.
(1)若到A处就购买,写出买到最低价格礼物的概率.
(2)小国同学的父亲认为,如果到A处不买,到B处发现比A处便宜就马上购买,否则到C处购买,这样更有希望买到最低价格的礼物.这个想法是否正确?试通过树状图分析说明.
解:(1)∵在每一处都有价格最低,最高,较高的可能,
∴P(A处买到最低价格礼物)=.
(2)作出树状图如下:
由树状图可知P购到最低价格礼物==.
∵>,∴他的想法是正确的.
由树状图可知P(购到最低价格礼物)==.
∵>,∴他的想法是正确的.
依据概率确定数量
2.在围棋盒中有x颗白色棋子和y颗黑色棋子,从盒中随机取出一颗棋子,取得白色棋子的概率是.若再往盒中放进6颗黑色棋子,取得白色棋子的概率是,则原来盒中有白色棋子 4 颗.
4
利用频率估计概率,估计总体数目
3.某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了如图所示的统计图,根据统计图提供的信息解决下列问题:
(1)这种树苗成活的频率稳定在 0.9 ,成活的概率估计值为 0.9 ;
(2)该地区已经移植这种树苗5万棵.
①估计这种树苗成活 4.5 万棵;
②如果该地区计划成活18万棵这种树苗,那么还需移植这种树苗约 15 万棵.
0.9
0.9
4.5
15
4.王强与李刚两位同学在学习“概率”时,做抛骰子(均匀正方体形状)试验,他们共抛了54次,出现向上点数的次数如下表:
向上点数 1 2 3 4 5 6
出现次数 6 9 5 8 16 10
(1)出现向上点数为3的频率为 ,出现向上点数为5的频率为 ;
(2)王强说:“根据试验,一次试验中出现向上点数为5的概率最大.”
李刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”
请判断王强和李刚说法的对错;
(3)如果王强与李刚各抛一枚骰子,则出现向上点数之和为3的倍数的概率为 .
解:(1);.
(2)因为抛一次骰子出现点数1,2,3,4,5,6向上具有等可能性,所以王强的说法不对,虽然抛54次出现点数6向上的频数是,但只抛54次的频率不一定等于概率,因为抛一次骰子,点数6向上的概率是,所以李刚的说法也不正确.
(3).
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
