能力微专训1——四大常考相似模型课件 北师大版九年级上册数学(32张PPT)
文档属性
| 名称 | 能力微专训1——四大常考相似模型课件 北师大版九年级上册数学(32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-16 07:58:19 | ||
图片预览









文档简介
(共32张PPT)
第四章 图形的相似
能力微专训1——四大常考相似模型
图形的相似是平面几何中非常重要的内容,也是中考中常考的考点.三角形相似的判定方法有多种,解题时要合理选用判定方法.相似三角形的判定方法有平行法;三组对应边的比相等(类似于三角形全等的判定方法“SSS”);两组对应边的比相等,且夹角相等(类似于三角形全等的判定方法“SAS”);两角对应相等;直角三角形中斜边、直角边对应成比例(类似于直角三角形全等的判定方法“HL”).
本专题把相似三角形的基本图形归类成四大常考相似模型:A字型、X字型、旋转型和K字型(一线三等角型).
A字型
特征:有一个公共角.
(1)A字型
已知:DE∥BC.结论:==.
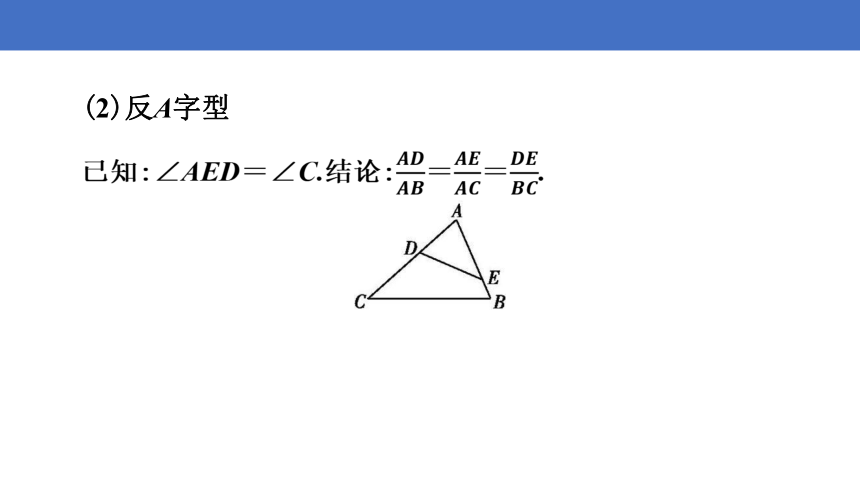
(2)反A字型
已知:∠AED=∠C.结论:==.
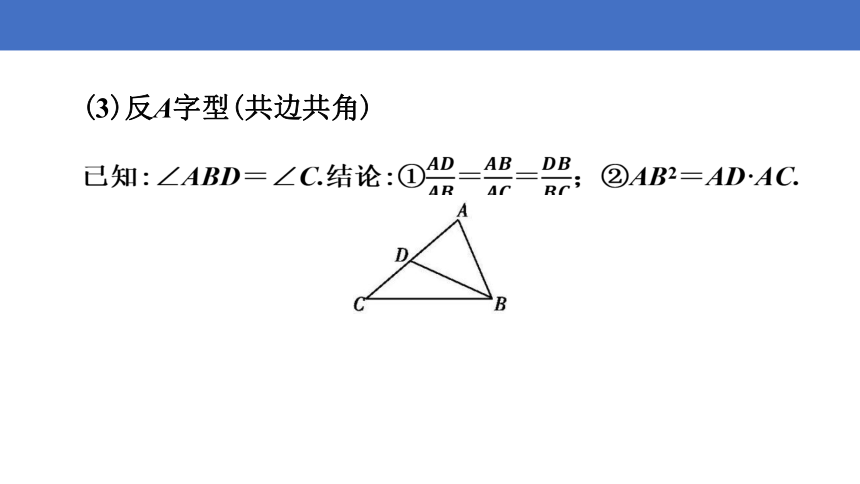
(3)反A字型(共边共角)
已知:∠ABD=∠C.结论:①==;②AB2=AD·AC.
(4)双垂直型
已知:△ABC是直角三角形,AD⊥BC.结论:①AB2=BD·BC;②AC2=CD·BC;③AD2=BD·CD.
【例1】如图,在△ABC中,P为边AB上一点,且∠ACP=∠B,若AP=2,BP=3,则AC的长为 .
提示:∵∠A=∠A,∠ACP=∠B,
∴△ABC∽△ACP,
∴=,
∴AC2=AP·AB=AP·(AP+BP)=2×(2+3)=10,
∴AC=.故答案为.
方法归纳交流 判断两个三角形相似,若已知一角对应相等,可先考虑另一角对应相等,注意公共角或对顶角或同角(等角)的余角(补角)相等.
变式训练 如图,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,若AD=1,BD=2,则的值为 .
X字型
特征:有一组隐含的等角(即对顶角相等).
(1)X字型
已知:AB∥CD.结论:==.
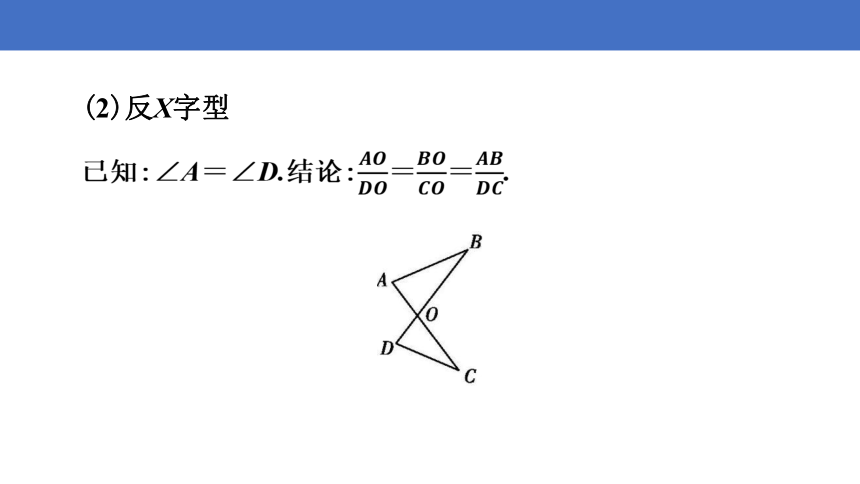
(2)反X字型
已知:∠A=∠D.结论:==.
【例2】如图,点E在平行四边形ABCD的边DC上,若DE∶EC=2∶3,则△AFB与△CFE的面积之比为 .
提示:在平行四边形ABCD中,AB∥CD,AB=CD.
∵DE∶EC=2∶3,
∴EC∶AB=3∶5.
∵AB∥CE,
∴△AFB∽△CFE,
∴==.
故答案为.
方法归纳交流 平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形相似.
变式训练 如图,AB∥CD,AD,BC相交于点E,过点E作EF∥CD交BD于点F,AB∶CD=2∶3,则EF∶AB= 3∶5 .
3∶5
旋转型
特征:有一个公共顶点的一组角相等.
(1)旋转不相交型
已知:∠BAC=∠DAE(或∠BAD=∠CAE),∠B=∠D.结论:△ABC∽△ADE.
(2)旋转相交型
已知:∠BAC=∠DAE(或∠BAD=∠CAE),∠B=∠D.结论:△ABC∽△ADE.
【例3】如图,∠DAB=∠EAC,∠ADE=∠ABC.
(1)求证:△ADE∽△ABC.
(2)求证:=.
证明:(1)∵∠DAB=∠EAC,
∴∠DAE=∠BAC.
又∵∠ADE=∠ABC,
∴△ADE∽△ABC.
(2)∵△ADE∽△ABC,∴=.
∵∠DAB=∠EAC,
∴△ADB∽△AEC,
∴=.
方法归纳交流
由已知∠DAB=∠EAC,根据角的和差可得∠DAE=∠BAC是解题的关键,两组对应角相等,三角形相似可证.
变式训练
如图,在△ABC与△ADE中,∠ACB=∠AED=90°,连接BD、CE,∠EAC=∠DAB.
(1)求证:△ABC∽△ADE.
(2)已知BC=4,AC=3,AE=,将△AED绕点A旋转,当点E落在线段CD上时,求BD的长.
解:(1)证明:∵∠EAC=∠DAB,
∴∠CAB=∠EAD.
∵∠ACB=∠AED=90°,
∴△ABC∽△ADE.
(2)∵∠ACB=90°,BC=4,AC=3,
∴AB===5.
∵△ABC∽△ADE,
∴=,
∴AD==.
∵∠EAC=∠DAB,
∴△CAE∽△BAD,
∴∠AEC=∠ADB.
如图,将△AED绕点A旋转,当点E落在线段CD上时,∠AEC=∠ADB=90°,
∴BD===.
K字型(一线三等角型)
特征:两个三角形的一条边在一条直线上,并且有一个顶点重合.
(1)一线三垂直型
已知:∠B=∠ACE=∠D=90°.结论:①△ABC∽△CDE;②AB·DE=BC·CD;③当C为BD中点时,△ABC∽△CDE∽△ACE.
(2)一线三等角型
已知:∠B=∠ACE=∠D=α.结论:①△ABC∽△CDE;②AB·DE=BC·CD;③当C为BD中点时,△ABC∽△CDE∽△ACE.
【例4】 如图,在△ABC中,AB=AC,点P,D分别是BC,AC边上的点,且∠APD=∠B.
(1)求证:△ABP∽△PCD.
(2)求证:AB·CD=CP·BP.
证明:(1)∵AB=AC,∴∠B=∠C.
∵∠APD=∠B,
∴∠APD=∠B=∠C.
∵∠APC=∠BAP+∠B,∠APC=∠APD+∠DPC,
∴∠BAP=∠CPD,
∴△ABP∽△PCD.
(2)∵△ABP∽△PCD,
∴=,
∴AB·CD=CP·BP.
变式训练 如图,在正方形ABCD中,M为BC上一点,MN⊥AM,MN交CD于点N.
(1)求证:△ABM∽△MCN.
(2)若AB=6,BM=2,求DN的长.
解:(1)证明:∵∠B=∠C=∠AMN=90°,
∴∠AMB+∠CMN=90°,∠CMN+∠MNC=90°,
∴∠AMB=∠MNC,
∴△ABM∽△MCN.
(2)由(1)可知△ABM∽△MCN,
∴=.
∵AB=BC=6,BM=2,
∴CM=4,
∴=,∴CN=,
∴DN=6-=.
第四章 图形的相似
能力微专训1——四大常考相似模型
图形的相似是平面几何中非常重要的内容,也是中考中常考的考点.三角形相似的判定方法有多种,解题时要合理选用判定方法.相似三角形的判定方法有平行法;三组对应边的比相等(类似于三角形全等的判定方法“SSS”);两组对应边的比相等,且夹角相等(类似于三角形全等的判定方法“SAS”);两角对应相等;直角三角形中斜边、直角边对应成比例(类似于直角三角形全等的判定方法“HL”).
本专题把相似三角形的基本图形归类成四大常考相似模型:A字型、X字型、旋转型和K字型(一线三等角型).
A字型
特征:有一个公共角.
(1)A字型
已知:DE∥BC.结论:==.
(2)反A字型
已知:∠AED=∠C.结论:==.
(3)反A字型(共边共角)
已知:∠ABD=∠C.结论:①==;②AB2=AD·AC.
(4)双垂直型
已知:△ABC是直角三角形,AD⊥BC.结论:①AB2=BD·BC;②AC2=CD·BC;③AD2=BD·CD.
【例1】如图,在△ABC中,P为边AB上一点,且∠ACP=∠B,若AP=2,BP=3,则AC的长为 .
提示:∵∠A=∠A,∠ACP=∠B,
∴△ABC∽△ACP,
∴=,
∴AC2=AP·AB=AP·(AP+BP)=2×(2+3)=10,
∴AC=.故答案为.
方法归纳交流 判断两个三角形相似,若已知一角对应相等,可先考虑另一角对应相等,注意公共角或对顶角或同角(等角)的余角(补角)相等.
变式训练 如图,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,若AD=1,BD=2,则的值为 .
X字型
特征:有一组隐含的等角(即对顶角相等).
(1)X字型
已知:AB∥CD.结论:==.
(2)反X字型
已知:∠A=∠D.结论:==.
【例2】如图,点E在平行四边形ABCD的边DC上,若DE∶EC=2∶3,则△AFB与△CFE的面积之比为 .
提示:在平行四边形ABCD中,AB∥CD,AB=CD.
∵DE∶EC=2∶3,
∴EC∶AB=3∶5.
∵AB∥CE,
∴△AFB∽△CFE,
∴==.
故答案为.
方法归纳交流 平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形相似.
变式训练 如图,AB∥CD,AD,BC相交于点E,过点E作EF∥CD交BD于点F,AB∶CD=2∶3,则EF∶AB= 3∶5 .
3∶5
旋转型
特征:有一个公共顶点的一组角相等.
(1)旋转不相交型
已知:∠BAC=∠DAE(或∠BAD=∠CAE),∠B=∠D.结论:△ABC∽△ADE.
(2)旋转相交型
已知:∠BAC=∠DAE(或∠BAD=∠CAE),∠B=∠D.结论:△ABC∽△ADE.
【例3】如图,∠DAB=∠EAC,∠ADE=∠ABC.
(1)求证:△ADE∽△ABC.
(2)求证:=.
证明:(1)∵∠DAB=∠EAC,
∴∠DAE=∠BAC.
又∵∠ADE=∠ABC,
∴△ADE∽△ABC.
(2)∵△ADE∽△ABC,∴=.
∵∠DAB=∠EAC,
∴△ADB∽△AEC,
∴=.
方法归纳交流
由已知∠DAB=∠EAC,根据角的和差可得∠DAE=∠BAC是解题的关键,两组对应角相等,三角形相似可证.
变式训练
如图,在△ABC与△ADE中,∠ACB=∠AED=90°,连接BD、CE,∠EAC=∠DAB.
(1)求证:△ABC∽△ADE.
(2)已知BC=4,AC=3,AE=,将△AED绕点A旋转,当点E落在线段CD上时,求BD的长.
解:(1)证明:∵∠EAC=∠DAB,
∴∠CAB=∠EAD.
∵∠ACB=∠AED=90°,
∴△ABC∽△ADE.
(2)∵∠ACB=90°,BC=4,AC=3,
∴AB===5.
∵△ABC∽△ADE,
∴=,
∴AD==.
∵∠EAC=∠DAB,
∴△CAE∽△BAD,
∴∠AEC=∠ADB.
如图,将△AED绕点A旋转,当点E落在线段CD上时,∠AEC=∠ADB=90°,
∴BD===.
K字型(一线三等角型)
特征:两个三角形的一条边在一条直线上,并且有一个顶点重合.
(1)一线三垂直型
已知:∠B=∠ACE=∠D=90°.结论:①△ABC∽△CDE;②AB·DE=BC·CD;③当C为BD中点时,△ABC∽△CDE∽△ACE.
(2)一线三等角型
已知:∠B=∠ACE=∠D=α.结论:①△ABC∽△CDE;②AB·DE=BC·CD;③当C为BD中点时,△ABC∽△CDE∽△ACE.
【例4】 如图,在△ABC中,AB=AC,点P,D分别是BC,AC边上的点,且∠APD=∠B.
(1)求证:△ABP∽△PCD.
(2)求证:AB·CD=CP·BP.
证明:(1)∵AB=AC,∴∠B=∠C.
∵∠APD=∠B,
∴∠APD=∠B=∠C.
∵∠APC=∠BAP+∠B,∠APC=∠APD+∠DPC,
∴∠BAP=∠CPD,
∴△ABP∽△PCD.
(2)∵△ABP∽△PCD,
∴=,
∴AB·CD=CP·BP.
变式训练 如图,在正方形ABCD中,M为BC上一点,MN⊥AM,MN交CD于点N.
(1)求证:△ABM∽△MCN.
(2)若AB=6,BM=2,求DN的长.
解:(1)证明:∵∠B=∠C=∠AMN=90°,
∴∠AMB+∠CMN=90°,∠CMN+∠MNC=90°,
∴∠AMB=∠MNC,
∴△ABM∽△MCN.
(2)由(1)可知△ABM∽△MCN,
∴=.
∵AB=BC=6,BM=2,
∴CM=4,
∴=,∴CN=,
∴DN=6-=.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
