【核心素养导向】北师大版九年级上册数学6.3 反比例函数的应用课件 (共20张PPT)
文档属性
| 名称 | 【核心素养导向】北师大版九年级上册数学6.3 反比例函数的应用课件 (共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-16 07:59:44 | ||
图片预览








文档简介
(共20张PPT)
第六章 反比例函数
3 反比例函数的应用
1.经历利用反比例函数解决实际问题的过程,体验函数思想的实用性.
2.在对反比例函数与一次函数的综合应用中,提高分析、综合的能力.
3.体会数形结合思想及函数思想的广泛应用.
◎重点:应用反比例函数的知识解决实际问题.
活动导入
期中考试刚刚结束,老师想让孩子们放松一下,于是决定带孩子们去上海迪士尼游玩,相约5月2日,在汇文学校门口集合,一起坐大巴前往,已知从汇文学校到上海迪士尼的路程约为360千米.
(1)大巴车的平均速度v km/h与时间t h之间有怎样的函数关系?
(2)原计划7点出发,12点到,但为了能多玩一会儿,提前1小时到达,平均车速应为多少?
(3)为了驾驶安全,车速不宜过快,若大巴车的平均车速不能超过80 km/h,那至少要几个小时才能到达到迪士尼?
生:(1)v和t之间的数量关系:vt=360,则v=.
(2)当t=4时,v===90.
师:请同学们讨论,尝试用不同的方法解决问题(3).
反比例函数的应用
阅读教材本课时相关内容,回答下列问题.
解一次函数与反比例函数相结合的题时,要充分利用“交点在两个函数的图象上”这个有利条件,一般地,两个函数,都对应着两个 函数图象 ,也就是对应着 两个方程 .还要充分利用正比例函数与反比例函数的图象都是 轴对称 图形与 中心 对称图形这个特点.
函数图象
两个方程
轴对称
中心
在教学过程中通过将问题分解,引导学生解题,培养学生思维的灵活性,向学生渗透“函数—方程—不等式”思想和“数形结合”的研究方法.
·导学建议·
1.如图,反比例函数y1=(x>0)和一次函数y2=x+1的图象相交于点A,则使y1>y2成立的x的取值范围是( B )
A.x>1 B.0<x<1
C.x<1 D.x>0
B
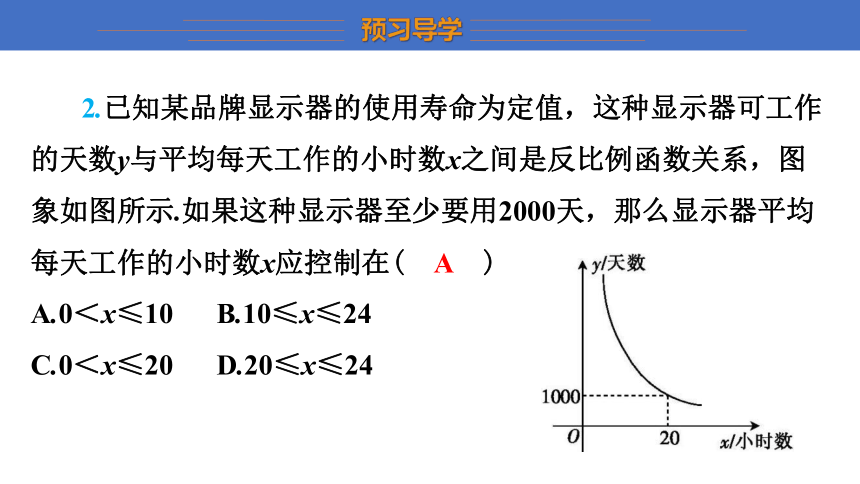
2.已知某品牌显示器的使用寿命为定值,这种显示器可工作的天数y与平均每天工作的小时数x之间是反比例函数关系,图象如图所示.如果这种显示器至少要用2000天,那么显示器平均每天工作的小时数x应控制在( A )
A.0<x≤10 B.10≤x≤24
C.0<x≤20 D.20≤x≤24
A
如果矩形的面积为6 cm2,那么它的长y (cm)与宽x (cm)之间的函数关系用图象表示大致是( C )
A B C D
C
由物理学知识可知,在力F(N)的作用下,物体会在力F的方向上发生位移s(m),力F所做的功W(J)满足:W=Fs.当W为定值时,F与s之间的函数图象如图所示.
(2)F与s之间的函数表达式为 F= .
(3)当F=4 N时,s是 m .
F=
m
(1)力F所做的功是 15 J .
15 J
如图,反比例函数y=的图象与一次函数y=mx+b的图象交于A(1,3),B(n,-1)两点.
(1)求反比例函数与一次函数的解析式;
(2)根据图象回答:当x取何值时,反比例函数的值大于一次函数的值.
解:(1)∵点A(1,3)在y=的图象上,∴k=3,∴y=.又∵点B(n,-1)在y=的图象上,
∴n=-3,即B(-3,-1),∴解得m=1,b=2,
∴反比例函数的解析式为y=,一次函数的解析式为y=x+2.
(2)从图象上可知,当x<-3或0<x<1时,反比例函数的值大于一次函数的值.
病人按规定的剂量服用某种药物,测得服药后2小时,每毫升血液中的含药量达到最大值为4毫克,已知服药后,2小时前每毫升血液中的含药量y(毫克)与时间x(小时)成正比例,2小时后y与x成反比例(如图).根据以上信息解答下列问题.
(1)求当0≤x≤2时,y与x的函数关系式;
(2)求当x>2时,y与x的函数关系式.
(3)若每毫升血液中的含药量不低于2毫克时治疗有效,则服药一次,治疗疾病的有效时间是多长?
解:(1)根据图象,正比例函数图象经过点(2,4),设函数解析式为y=kx,则2k=4,
解得k=2,所以函数关系为y=2x(0≤x≤2).
(2)根据图象,反比例函数图象经过点(2,4),设函数解析式为y=,则=4,解得k=8,
所以函数关系为y=(x>2).
(3)当y=2时,2x=2,解得x=1,=2,解得x=4,
所以服药一次,治疗疾病的有效时间是4-1=3(小时).
李先生参加了某电脑公司推出的分期付款购买电脑活动,他购买的电脑价格为1.2万元,交了首付之后每月付款y元,x月结清余款.y与x的函数关系如图所示,试根据图象提供的信息回答下列问题.
(1)确定y与x的函数关系式,并求出首付款的数目.
(2)李先生若用4个月结清余款,每月应付多少元?
(3)如打算每月付款不超过500元,李先生至少几个月才能结清余款?
解:(1)由图象可知y与x成反比例,设y与x的函数关系式为y=,把A(2,4000)代入关系式得4000=,∴k=8000,∴y=,∴12000-8000=4000(元).
(2)当x=4时,y==2000(元),
∴每月应付2000元.
(3)当y=500时,500=,∴x=16,∴李先生至少16个月才能结清余款.
第六章 反比例函数
3 反比例函数的应用
1.经历利用反比例函数解决实际问题的过程,体验函数思想的实用性.
2.在对反比例函数与一次函数的综合应用中,提高分析、综合的能力.
3.体会数形结合思想及函数思想的广泛应用.
◎重点:应用反比例函数的知识解决实际问题.
活动导入
期中考试刚刚结束,老师想让孩子们放松一下,于是决定带孩子们去上海迪士尼游玩,相约5月2日,在汇文学校门口集合,一起坐大巴前往,已知从汇文学校到上海迪士尼的路程约为360千米.
(1)大巴车的平均速度v km/h与时间t h之间有怎样的函数关系?
(2)原计划7点出发,12点到,但为了能多玩一会儿,提前1小时到达,平均车速应为多少?
(3)为了驾驶安全,车速不宜过快,若大巴车的平均车速不能超过80 km/h,那至少要几个小时才能到达到迪士尼?
生:(1)v和t之间的数量关系:vt=360,则v=.
(2)当t=4时,v===90.
师:请同学们讨论,尝试用不同的方法解决问题(3).
反比例函数的应用
阅读教材本课时相关内容,回答下列问题.
解一次函数与反比例函数相结合的题时,要充分利用“交点在两个函数的图象上”这个有利条件,一般地,两个函数,都对应着两个 函数图象 ,也就是对应着 两个方程 .还要充分利用正比例函数与反比例函数的图象都是 轴对称 图形与 中心 对称图形这个特点.
函数图象
两个方程
轴对称
中心
在教学过程中通过将问题分解,引导学生解题,培养学生思维的灵活性,向学生渗透“函数—方程—不等式”思想和“数形结合”的研究方法.
·导学建议·
1.如图,反比例函数y1=(x>0)和一次函数y2=x+1的图象相交于点A,则使y1>y2成立的x的取值范围是( B )
A.x>1 B.0<x<1
C.x<1 D.x>0
B
2.已知某品牌显示器的使用寿命为定值,这种显示器可工作的天数y与平均每天工作的小时数x之间是反比例函数关系,图象如图所示.如果这种显示器至少要用2000天,那么显示器平均每天工作的小时数x应控制在( A )
A.0<x≤10 B.10≤x≤24
C.0<x≤20 D.20≤x≤24
A
如果矩形的面积为6 cm2,那么它的长y (cm)与宽x (cm)之间的函数关系用图象表示大致是( C )
A B C D
C
由物理学知识可知,在力F(N)的作用下,物体会在力F的方向上发生位移s(m),力F所做的功W(J)满足:W=Fs.当W为定值时,F与s之间的函数图象如图所示.
(2)F与s之间的函数表达式为 F= .
(3)当F=4 N时,s是 m .
F=
m
(1)力F所做的功是 15 J .
15 J
如图,反比例函数y=的图象与一次函数y=mx+b的图象交于A(1,3),B(n,-1)两点.
(1)求反比例函数与一次函数的解析式;
(2)根据图象回答:当x取何值时,反比例函数的值大于一次函数的值.
解:(1)∵点A(1,3)在y=的图象上,∴k=3,∴y=.又∵点B(n,-1)在y=的图象上,
∴n=-3,即B(-3,-1),∴解得m=1,b=2,
∴反比例函数的解析式为y=,一次函数的解析式为y=x+2.
(2)从图象上可知,当x<-3或0<x<1时,反比例函数的值大于一次函数的值.
病人按规定的剂量服用某种药物,测得服药后2小时,每毫升血液中的含药量达到最大值为4毫克,已知服药后,2小时前每毫升血液中的含药量y(毫克)与时间x(小时)成正比例,2小时后y与x成反比例(如图).根据以上信息解答下列问题.
(1)求当0≤x≤2时,y与x的函数关系式;
(2)求当x>2时,y与x的函数关系式.
(3)若每毫升血液中的含药量不低于2毫克时治疗有效,则服药一次,治疗疾病的有效时间是多长?
解:(1)根据图象,正比例函数图象经过点(2,4),设函数解析式为y=kx,则2k=4,
解得k=2,所以函数关系为y=2x(0≤x≤2).
(2)根据图象,反比例函数图象经过点(2,4),设函数解析式为y=,则=4,解得k=8,
所以函数关系为y=(x>2).
(3)当y=2时,2x=2,解得x=1,=2,解得x=4,
所以服药一次,治疗疾病的有效时间是4-1=3(小时).
李先生参加了某电脑公司推出的分期付款购买电脑活动,他购买的电脑价格为1.2万元,交了首付之后每月付款y元,x月结清余款.y与x的函数关系如图所示,试根据图象提供的信息回答下列问题.
(1)确定y与x的函数关系式,并求出首付款的数目.
(2)李先生若用4个月结清余款,每月应付多少元?
(3)如打算每月付款不超过500元,李先生至少几个月才能结清余款?
解:(1)由图象可知y与x成反比例,设y与x的函数关系式为y=,把A(2,4000)代入关系式得4000=,∴k=8000,∴y=,∴12000-8000=4000(元).
(2)当x=4时,y==2000(元),
∴每月应付2000元.
(3)当y=500时,500=,∴x=16,∴李先生至少16个月才能结清余款.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
