【核心素养导向】北师大版九年级下册数学1.3 三角函数的计算 课件 (共22张PPT)
文档属性
| 名称 | 【核心素养导向】北师大版九年级下册数学1.3 三角函数的计算 课件 (共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 839.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-16 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
第一章 直角三角形的边角关系
3 三角函数的计算
1.会运用计算器解决由已知锐角求三角函数值,由三角函数值求相应锐角的度数等数学问题.
2.能在简单的实际问题中找到垂直关系,构建含三角函数关系的数学模型.
◎重点:运用计算器解决与三角函数有关的计算.
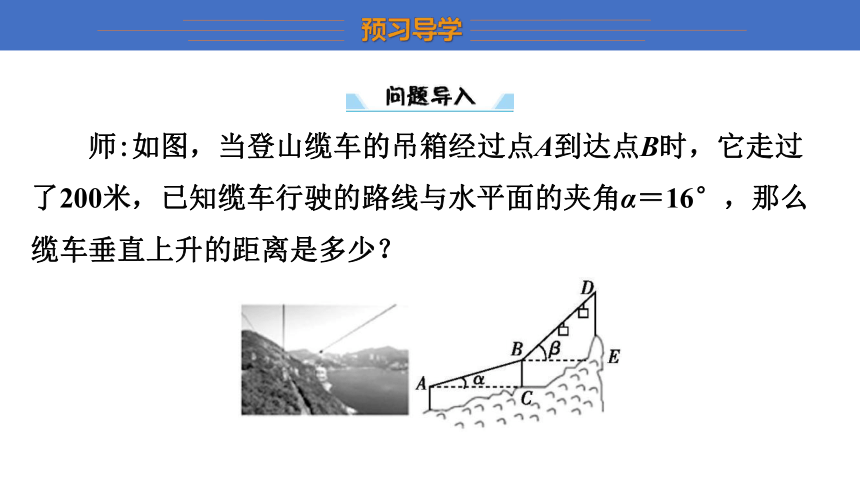
师:如图,当登山缆车的吊箱经过点A到达点B时,它走过了200米,已知缆车行驶的路线与水平面的夹角α=16°,那么缆车垂直上升的距离是多少?
生:在Rt△ABC中,α=16°,AB=200米,需求出BC.根据正弦的定义,sin 16°==,∴BC=ABsin 16°=(200sin 16°)米.
师:200sin 16° 米中的“sin 16°”是多少呢?我们知道,在三角函数中,当角的大小确定时,三角函数值与直角三角形的大小无关,随角度的确定而确定.
对于特殊角30°、45°、60°,可以根据勾股定理和含这些特殊角的直角三角形的性质,求出它们的三角函数值.而对于一般锐角的三角函数值,我们需借助于科学计算器求出这些锐角的三角函数值.
怎样用科学计算器求三角函数值呢?
用计算器计算三角函数值
阅读教材本课时“想一想”及其前面的内容,完成下列问题.
(1)如果锐角α恰是整数度数或小数度数时,只需按sin、cos或tan键,再按数字键即可.
利用计算器由三角函数值求相应的锐角
阅读教材本课时“想一想”后面的内容,完成下列问题.
利用计算器,由一个锐角的三角函数值,求相应锐角的度数步骤.
(1)已知三角函数值,求锐角度数,要用到sin、cos、tan键的第二功能 sin-1 、 cos-2 、 tan-1 和SHIFT键.
sin-1
cos-2
tan-1
(2)按键顺序是先按SHIFT,再按sin、cos或tan键,然后按 数字 ,最后按等号.
数字
在学生边阅读、边计算时,教师要提醒学生以下几点:在按sin-1或cos-1或tan-1键前必须按第二功能选择键;计算器显示得到的结果是这个锐角的度数,必须按课本上的方法逐一把度数的小数部分化为分,再把分的小数部分化为秒,最后得到精确到1″的锐角的近似角.
·导学建议·
利用三角函数解决实际问题.
如图,一斜坡上铅垂的两棵树间的水平距离AB=4米,斜面距离BC=4.25米,求坡角∠D的度数.(结果精确到1°)
解:cos∠ABC=≈0.94,∠ABC≈20°,∴∠D=∠ABC≈20°.
用计算器求下列各式的值:(1)sin 20°;(2)cos 38°;(3)tan 10°;(4)tan 80°;(5)cos 27°51';(6)tan 56°17'35″;(7)sin 75°31'12″;(8)3sin 29°.
解:(1)0.3420;(2)0.7880;(3)0.1763;(4)5.6713;(5)0.8842;(6)1.4990;(7)0.9682;(8)1.4544.
如图,为了测量某建筑物的高AB,在距离B点35米的D处安置测角仪,测得A点的仰角α为47°,若仪器CD高为1.4米,求建筑物的高AB.(结果精确到0.01米)
解:如图,过点C作CE⊥AB于点E.根据题意,在Rt△ACE中,AE=CE×tan 47°≈35×1.0724=37.534≈37.53 m,AB=AE+EB=AE+CD=37.53+1.4=38.93 m.
因此建筑物的高AB约为38.93 m.
方法归纳交流 当锐角A是30°、45°或60°的特殊角时,可以求得这些角的三角函数值;但如果不是这些特殊角时,一般借助计算器求解三角函数值.已知三角函数值求锐角的关键是要进行功能转换,即先按功能转换键,计算器显示出结果后,要把秒按四舍五入取近似值,写出最后结果.
分别求下列锐角θ的大小:(1)tan θ=2.9888;(2)sin θ=0.3957;(3)cos θ=0.7850.
解:(1)θ=71°30'2″;(2)θ=23°18'35″;(3)θ=38°16'46″.
一辆汽车沿着一山坡行驶了150米,其铅直高度上升了25米,求山坡与水平面所成锐角的大小?
解:设山坡与水平面所成的锐角为α,根据题意得sin α==,∴α=9°35'39″.∴山坡与水平面所成的锐角为9°35'39″.
如图,一个人从山底爬到山顶,需先爬坡角为40°的山坡300 m,再爬坡角为30°的山坡100 m,求山高.(结果精确到0.1 m)
解:根据题意,可得BC=300 m,BA=100 m,∠C=40°,∠ABF=30°.
在Rt△CBD中,BD=BC·sin 40°≈300×0.6428≈192.8 m;
在Rt△ABF中,AF=ABsin 30°=100×0.5=50 m.
所以山高AE=AF+BD=192.8+50=242.8 m.
1.已知sin A=0.3239,则锐角A约为( C )
A.17° B.18° C.19° D.71°
C
2.求下列各式中的锐角α(精确到分).
(1)cos(2α-24°)=0.8480;(2)=2.726.
解:(1)因为2α-24°=32°,所以锐角α为28°.
(2)因为=2.726,所以3cos α=2.726.即cos α=≈0.9087.所以锐角α为24°40'25″.
第一章 直角三角形的边角关系
3 三角函数的计算
1.会运用计算器解决由已知锐角求三角函数值,由三角函数值求相应锐角的度数等数学问题.
2.能在简单的实际问题中找到垂直关系,构建含三角函数关系的数学模型.
◎重点:运用计算器解决与三角函数有关的计算.
师:如图,当登山缆车的吊箱经过点A到达点B时,它走过了200米,已知缆车行驶的路线与水平面的夹角α=16°,那么缆车垂直上升的距离是多少?
生:在Rt△ABC中,α=16°,AB=200米,需求出BC.根据正弦的定义,sin 16°==,∴BC=ABsin 16°=(200sin 16°)米.
师:200sin 16° 米中的“sin 16°”是多少呢?我们知道,在三角函数中,当角的大小确定时,三角函数值与直角三角形的大小无关,随角度的确定而确定.
对于特殊角30°、45°、60°,可以根据勾股定理和含这些特殊角的直角三角形的性质,求出它们的三角函数值.而对于一般锐角的三角函数值,我们需借助于科学计算器求出这些锐角的三角函数值.
怎样用科学计算器求三角函数值呢?
用计算器计算三角函数值
阅读教材本课时“想一想”及其前面的内容,完成下列问题.
(1)如果锐角α恰是整数度数或小数度数时,只需按sin、cos或tan键,再按数字键即可.
利用计算器由三角函数值求相应的锐角
阅读教材本课时“想一想”后面的内容,完成下列问题.
利用计算器,由一个锐角的三角函数值,求相应锐角的度数步骤.
(1)已知三角函数值,求锐角度数,要用到sin、cos、tan键的第二功能 sin-1 、 cos-2 、 tan-1 和SHIFT键.
sin-1
cos-2
tan-1
(2)按键顺序是先按SHIFT,再按sin、cos或tan键,然后按 数字 ,最后按等号.
数字
在学生边阅读、边计算时,教师要提醒学生以下几点:在按sin-1或cos-1或tan-1键前必须按第二功能选择键;计算器显示得到的结果是这个锐角的度数,必须按课本上的方法逐一把度数的小数部分化为分,再把分的小数部分化为秒,最后得到精确到1″的锐角的近似角.
·导学建议·
利用三角函数解决实际问题.
如图,一斜坡上铅垂的两棵树间的水平距离AB=4米,斜面距离BC=4.25米,求坡角∠D的度数.(结果精确到1°)
解:cos∠ABC=≈0.94,∠ABC≈20°,∴∠D=∠ABC≈20°.
用计算器求下列各式的值:(1)sin 20°;(2)cos 38°;(3)tan 10°;(4)tan 80°;(5)cos 27°51';(6)tan 56°17'35″;(7)sin 75°31'12″;(8)3sin 29°.
解:(1)0.3420;(2)0.7880;(3)0.1763;(4)5.6713;(5)0.8842;(6)1.4990;(7)0.9682;(8)1.4544.
如图,为了测量某建筑物的高AB,在距离B点35米的D处安置测角仪,测得A点的仰角α为47°,若仪器CD高为1.4米,求建筑物的高AB.(结果精确到0.01米)
解:如图,过点C作CE⊥AB于点E.根据题意,在Rt△ACE中,AE=CE×tan 47°≈35×1.0724=37.534≈37.53 m,AB=AE+EB=AE+CD=37.53+1.4=38.93 m.
因此建筑物的高AB约为38.93 m.
方法归纳交流 当锐角A是30°、45°或60°的特殊角时,可以求得这些角的三角函数值;但如果不是这些特殊角时,一般借助计算器求解三角函数值.已知三角函数值求锐角的关键是要进行功能转换,即先按功能转换键,计算器显示出结果后,要把秒按四舍五入取近似值,写出最后结果.
分别求下列锐角θ的大小:(1)tan θ=2.9888;(2)sin θ=0.3957;(3)cos θ=0.7850.
解:(1)θ=71°30'2″;(2)θ=23°18'35″;(3)θ=38°16'46″.
一辆汽车沿着一山坡行驶了150米,其铅直高度上升了25米,求山坡与水平面所成锐角的大小?
解:设山坡与水平面所成的锐角为α,根据题意得sin α==,∴α=9°35'39″.∴山坡与水平面所成的锐角为9°35'39″.
如图,一个人从山底爬到山顶,需先爬坡角为40°的山坡300 m,再爬坡角为30°的山坡100 m,求山高.(结果精确到0.1 m)
解:根据题意,可得BC=300 m,BA=100 m,∠C=40°,∠ABF=30°.
在Rt△CBD中,BD=BC·sin 40°≈300×0.6428≈192.8 m;
在Rt△ABF中,AF=ABsin 30°=100×0.5=50 m.
所以山高AE=AF+BD=192.8+50=242.8 m.
1.已知sin A=0.3239,则锐角A约为( C )
A.17° B.18° C.19° D.71°
C
2.求下列各式中的锐角α(精确到分).
(1)cos(2α-24°)=0.8480;(2)=2.726.
解:(1)因为2α-24°=32°,所以锐角α为28°.
(2)因为=2.726,所以3cos α=2.726.即cos α=≈0.9087.所以锐角α为24°40'25″.
