24.1.4圆周角
图片预览






文档简介
课件25张PPT。24.1.4 圆周角第24章 圆1、复习提问:(2)圆心角,弧,弦,弦心
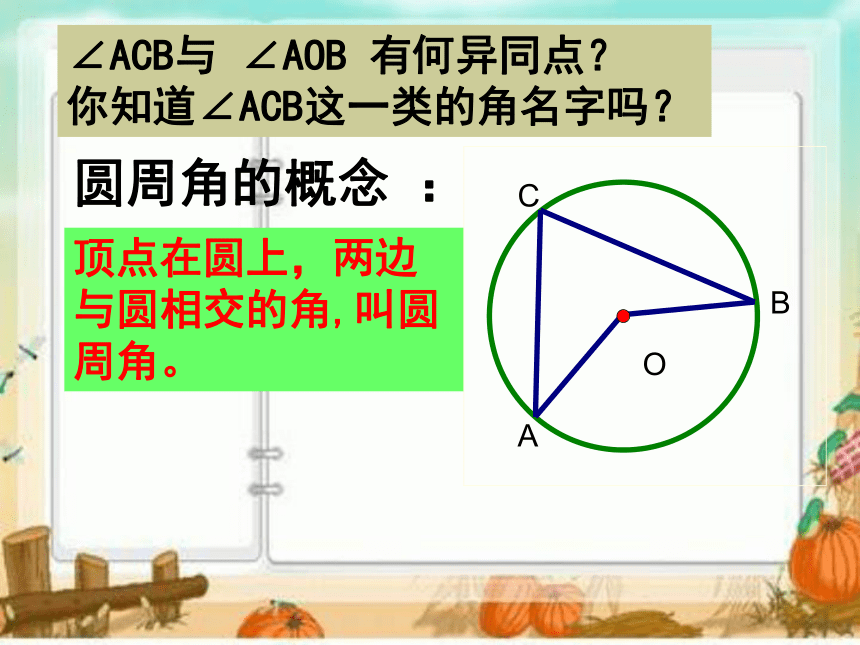
距关系定理是什么? (1)什么是圆心角?∠ACB与 ∠AOB 有何异同点?
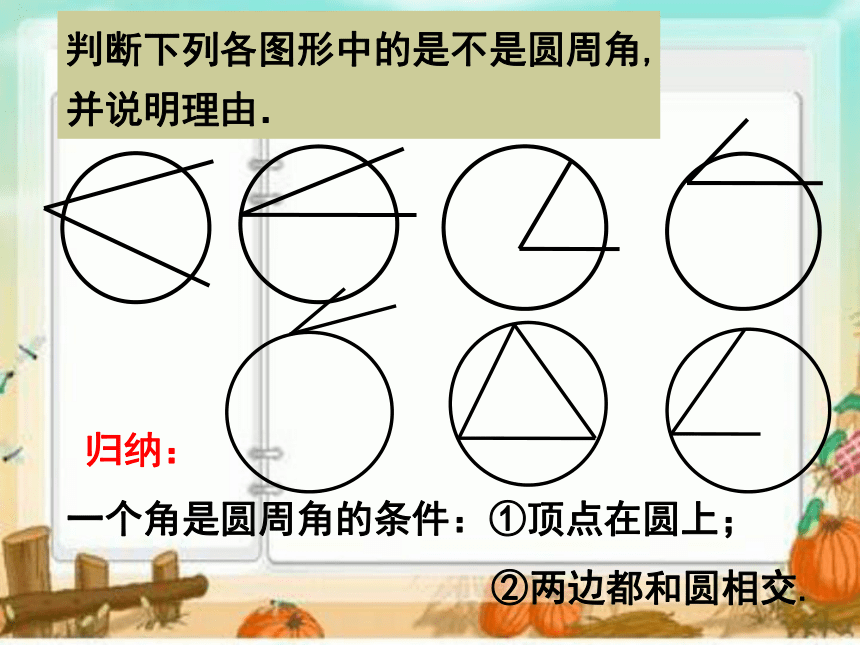
你知道∠ACB这一类的角名字吗? 顶点在圆上,两边与圆相交的角,叫圆周角。 圆周角的概念 : 判断下列各图形中的是不是圆周角,
并说明理由. 归纳:
一个角是圆周角的条件:①顶点在圆上;
②两边都和圆相交.问题:圆周角的度数与相应的圆心角度数有
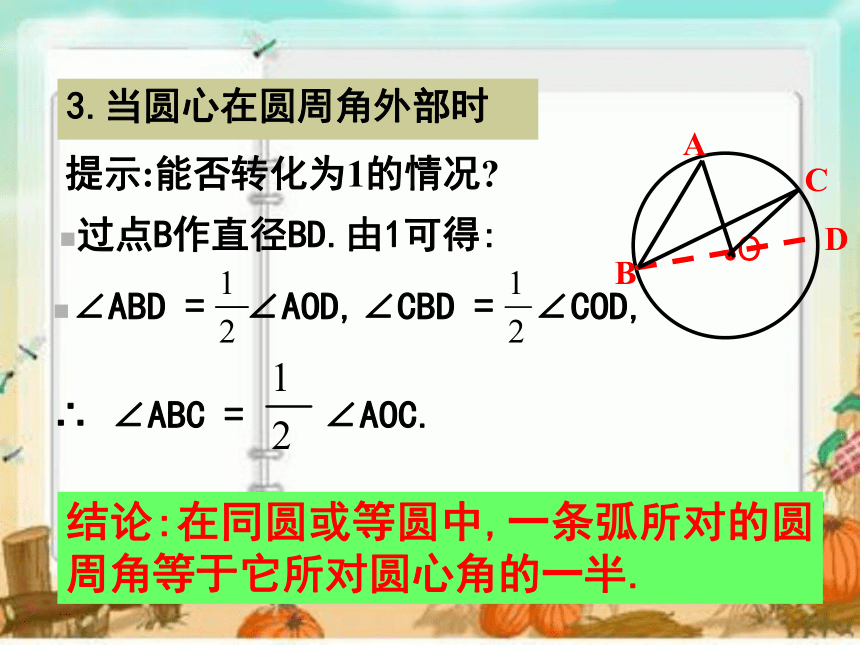
什么关系?(1)当圆心在圆周角的一边上时,探究一:证明:(圆心在圆周角上) 结论:在同圆或等圆中,一条弧所对的圆周角等于它所对圆心角的一半.COBA2.当圆心在圆周角内部时提示:能否转化为1的情况?过点B作直径BD.由1可得: ∴ ∠ABC = ∠AOC.∠ABD = ∠AOD,∠CBD = ∠COD,结论:在同圆或等圆中,一条弧所对的圆周角等于它所对圆心角的一半. 3.当圆心在圆周角外部时结论:在同圆或等圆中,一条弧所对的圆周角等于它所对圆心角的一半. 提示:能否转化为1的情况?过点B作直径BD.由1可得: ∴ ∠ABC = ∠AOC.∠ABD = ∠AOD,∠CBD = ∠COD,D圆周角定理1,在同圆或等圆中,一条弧所对的圆周角等于它所对圆心角的一半.
2,在同圆或等圆中,同弧或等弧所对的圆周角相等1.半圆或直径所对的圆周角等于多少度?推论:
半圆或直径所对的圆周角都相等,都等于90°(直角).反过来也是成立的,即90°的圆周角所对的弦是圆的直径探究二:OABC2. 90°的圆周角所对的弦是
否是直径?如果∠A=44°,则∠BOC=____.
如果∠BOC=44°,则∠A=____.
如果∠A=35°,则∠BDC=____.LIAN练习xi如图,点E、F、G、H在圆 上,
你会找出几对相等的圆周 角?思考:1、在同圆或等圆中,如果两个圆周角相等,它们所对的弧一定相等吗?为什么?2、在一个圆中,一条弦所对有几种圆周角,它们有什么关系?结论:在同圆或等圆中,如果两个圆周角相 等,
它们所对的弧相等。有两种相等或互补例题讲解例.如图⊙o的直径AB为10cm,弦AC为6cm,
∠ACB的平分线交⊙o于点D,求BC,AD,BD的长.练习:1,如图 AB是⊙O的直径, C ,D是圆上的两点,若∠ABD=40°,则∠BCD=_____.40°5002. 如图OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC.
求证:∠ABC=∠BAC.3,如图所示,AB,AC是⊙O的弦,AD⊥BC于D,交⊙O于F,AE与⊙O的直径,试问两弦BE与CF的大小有何关系,说明理由.
4,已知:△ABC的三个顶点在⊙O上,
∠BAC=50°,∠ABC=47°,求∠AOB.解:有题意知:∠A、∠B、∠C是圆周角,
∠AOB是圆心角.
又∵∠BAC=50°,∠ABC=47° ∴∠ACB=180°-(∠A+∠B)
=180°-(50°+47°)
=83°.∴ ∠AOB=2∠ACB=2×83°=166°.5,求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。(提示:作出这条边为直径的圆)OABC6,如图,已知圆心角∠AOB=100°,求圆周角∠ACB、∠ADB的度数?
7,一条弦分圆为1:4两部分,求这弦所对的圆周角的度数?CDABE补充例题:
平分已知弧AB已知:弧AB作法:⒈ 连结AB.⒉作AB的垂直平分线 CD,交弧AB于点E.∴点E就是所求弧AB的中点。求作:弧AB的中点.你能破镜重圆吗?ABACmn·O 作弦AB.AC及它们的垂直平分线m.n,交于O点;以O为圆心,OA为半径作圆。破镜重圆ABCmn·O 弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
作图依据:4、在圆中,一条弧所对的圆心角和 圆周角分别为(2x+100)°和 (5x—30)°,求这条弧所对的圆心角和圆周角的度数。 学生练习已知:如图,AB是⊙O直径,与CD相交于点E,已知AE=1cm,BE=5cm, ∠DEB=600,求弦CD的长..OCDABE1.如图,∠A是圆O的圆周角, ∠A=40°,求∠OBC的度数。 巩固练习
距关系定理是什么? (1)什么是圆心角?∠ACB与 ∠AOB 有何异同点?
你知道∠ACB这一类的角名字吗? 顶点在圆上,两边与圆相交的角,叫圆周角。 圆周角的概念 : 判断下列各图形中的是不是圆周角,
并说明理由. 归纳:
一个角是圆周角的条件:①顶点在圆上;
②两边都和圆相交.问题:圆周角的度数与相应的圆心角度数有
什么关系?(1)当圆心在圆周角的一边上时,探究一:证明:(圆心在圆周角上) 结论:在同圆或等圆中,一条弧所对的圆周角等于它所对圆心角的一半.COBA2.当圆心在圆周角内部时提示:能否转化为1的情况?过点B作直径BD.由1可得: ∴ ∠ABC = ∠AOC.∠ABD = ∠AOD,∠CBD = ∠COD,结论:在同圆或等圆中,一条弧所对的圆周角等于它所对圆心角的一半. 3.当圆心在圆周角外部时结论:在同圆或等圆中,一条弧所对的圆周角等于它所对圆心角的一半. 提示:能否转化为1的情况?过点B作直径BD.由1可得: ∴ ∠ABC = ∠AOC.∠ABD = ∠AOD,∠CBD = ∠COD,D圆周角定理1,在同圆或等圆中,一条弧所对的圆周角等于它所对圆心角的一半.
2,在同圆或等圆中,同弧或等弧所对的圆周角相等1.半圆或直径所对的圆周角等于多少度?推论:
半圆或直径所对的圆周角都相等,都等于90°(直角).反过来也是成立的,即90°的圆周角所对的弦是圆的直径探究二:OABC2. 90°的圆周角所对的弦是
否是直径?如果∠A=44°,则∠BOC=____.
如果∠BOC=44°,则∠A=____.
如果∠A=35°,则∠BDC=____.LIAN练习xi如图,点E、F、G、H在圆 上,
你会找出几对相等的圆周 角?思考:1、在同圆或等圆中,如果两个圆周角相等,它们所对的弧一定相等吗?为什么?2、在一个圆中,一条弦所对有几种圆周角,它们有什么关系?结论:在同圆或等圆中,如果两个圆周角相 等,
它们所对的弧相等。有两种相等或互补例题讲解例.如图⊙o的直径AB为10cm,弦AC为6cm,
∠ACB的平分线交⊙o于点D,求BC,AD,BD的长.练习:1,如图 AB是⊙O的直径, C ,D是圆上的两点,若∠ABD=40°,则∠BCD=_____.40°5002. 如图OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC.
求证:∠ABC=∠BAC.3,如图所示,AB,AC是⊙O的弦,AD⊥BC于D,交⊙O于F,AE与⊙O的直径,试问两弦BE与CF的大小有何关系,说明理由.
4,已知:△ABC的三个顶点在⊙O上,
∠BAC=50°,∠ABC=47°,求∠AOB.解:有题意知:∠A、∠B、∠C是圆周角,
∠AOB是圆心角.
又∵∠BAC=50°,∠ABC=47° ∴∠ACB=180°-(∠A+∠B)
=180°-(50°+47°)
=83°.∴ ∠AOB=2∠ACB=2×83°=166°.5,求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。(提示:作出这条边为直径的圆)OABC6,如图,已知圆心角∠AOB=100°,求圆周角∠ACB、∠ADB的度数?
7,一条弦分圆为1:4两部分,求这弦所对的圆周角的度数?CDABE补充例题:
平分已知弧AB已知:弧AB作法:⒈ 连结AB.⒉作AB的垂直平分线 CD,交弧AB于点E.∴点E就是所求弧AB的中点。求作:弧AB的中点.你能破镜重圆吗?ABACmn·O 作弦AB.AC及它们的垂直平分线m.n,交于O点;以O为圆心,OA为半径作圆。破镜重圆ABCmn·O 弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
作图依据:4、在圆中,一条弧所对的圆心角和 圆周角分别为(2x+100)°和 (5x—30)°,求这条弧所对的圆心角和圆周角的度数。 学生练习已知:如图,AB是⊙O直径,与CD相交于点E,已知AE=1cm,BE=5cm, ∠DEB=600,求弦CD的长..OCDABE1.如图,∠A是圆O的圆周角, ∠A=40°,求∠OBC的度数。 巩固练习
同课章节目录
